Chapitre 16
Synthèse
Triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
Dans chaque cas, donner la nature du
triangle \mathrm{ABC}.
1. \widehat{\mathrm{ABC}}=56^{\circ} et \widehat{\mathrm{BAC}}=34^{\circ}.
2. \widehat{\mathrm{ABC}}=60^{\circ} et \widehat{\mathrm{BAC}}=60^{\circ}.
3. \widehat{\mathrm{ABC}}=106^{\circ} et \widehat{\mathrm{BAC}}=37^{\circ}.
4. \widehat{\mathrm{ABC}}=32^{\circ} et \widehat{\mathrm{BAC}}=74^{\circ}.
5. \widehat{\mathrm{ABC}}=21^{\circ} et \widehat{\mathrm{BAC}}=21^{\circ}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
\mathrm{RST} est un triangle rectangle et isocèle en \mathrm{T}.
Déterminer la mesure de ses trois angles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Les questions suivantes sont indépendantes,
mais utilisent le même quadrilatère ci-dessous.

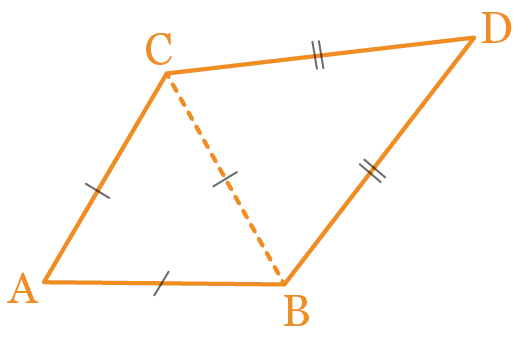
1. Sachant que les segments [\mathrm{AB}] et [\mathrm{BD}] mesurent respectivement 7 \mathrm{cm} et 11 \mathrm{cm}, calculer le périmètre du quadrilatère \mathrm{ABDC}.


1. Sachant que les segments [\mathrm{AB}] et [\mathrm{BD}] mesurent respectivement 7 \mathrm{cm} et 11 \mathrm{cm}, calculer le périmètre du quadrilatère \mathrm{ABDC}.
2. Sachant que \mathrm{CB}=5 \mathrm{~cm} et que le périmètre
de \mathrm{BCD} est 17 \mathrm{cm}, calculer le périmètre du
quadrilatère \mathrm{ABDC}.
3. Sachant que le périmètre du triangle \mathrm{ABC}
est de 18 \mathrm{cm} et que celui du triangle \mathrm{BCD}
est de 16 \mathrm{cm}, calculer le périmètre du
quadrilatère \mathrm{ABDC}.
4. Sachant que le périmètre de \mathrm{ABDC} est
de 25 \mathrm{cm} et que celui de \mathrm{ABC} est de 12 \mathrm{cm},
calculer la longueur du segment [\mathrm{CD}].
5. Sachant que le périmètre de \mathrm{ABDC} est
de 38 \mathrm{cm} et que le périmètre de \mathrm{BCD} est
de 29 \mathrm{cm}, calculer le périmètre de \mathrm{ABC}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Voici un programme de construction.
1. Réaliser un schéma à main levée.
2. Réaliser la figure en vraie grandeur.
3. En justifiant, déterminer la nature du triangle \mathrm{GFE}.
- Tracer le segment [\mathrm{GF}] de longueur 7,5 \mathrm{cm}.
- Tracer la demi-droite [\mathrm{F} x) telle que \widehat{\mathrm{GFx}}=27^{\circ}.
- Tracer la demi-droite [\mathrm{G} y) qui coupe [\mathrm{F} x) telle que \widehat{\mathrm{FG} y}=63^{\circ}.
- Placer le point \mathrm{E} à l'intersection des deux demi-droites.
1. Réaliser un schéma à main levée.
Cliquez ici pour avoir accès à un espace de dessin
2. Réaliser la figure en vraie grandeur.
Cliquez pour accéder à GeoGebra
3. En justifiant, déterminer la nature du triangle \mathrm{GFE}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
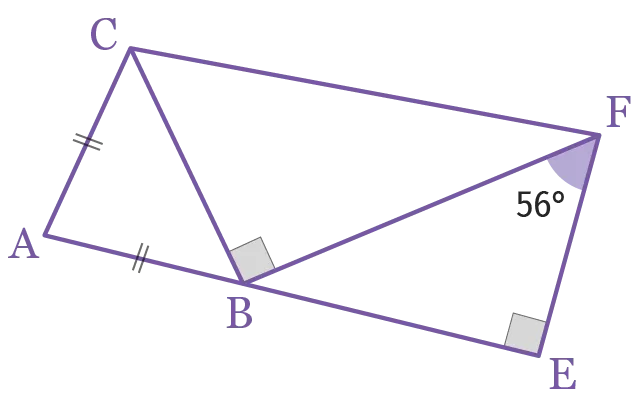
Quelle mesure doit avoir l'angle \widehat{\mathrm{CAB}} afin
que les points \mathrm{A}, \mathrm{B} et \mathrm{E} soient alignés ?
Justifier.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
On considère la figure ci-dessous.

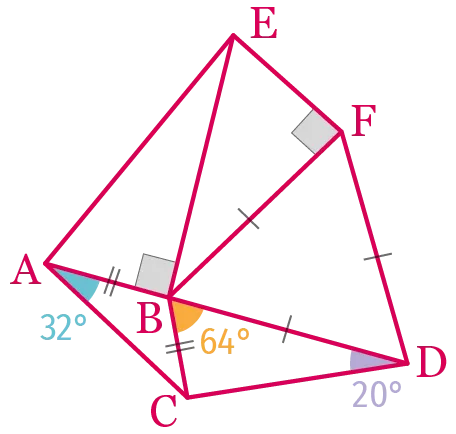
2. Calculer la mesure de l'angle \widehat{\mathrm{BEF}}.


1.
a. Calculer la mesure de l'angle \widehat{\mathrm{ABC}}.
b. En déduire que les points \mathrm{A}, \mathrm{B} et \mathrm{D} sont
alignés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[\mathrm{BC}] est un diamètre du cercle de centre \mathrm{A}.
\mathrm{D} est un point quelconque appartenant
à ce cercle. Le but de cet exercice est de
déterminer la nature du triangle \mathrm{BCD}.

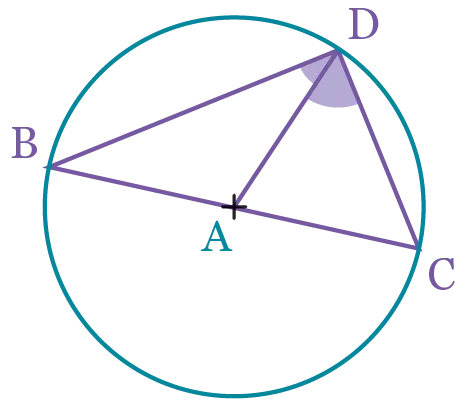


1. En utilisant les propriétés du cercle,
déterminer la nature des triangles \mathrm{ABD} et
\mathrm{ACD}.
2. En se plaçant dans le triangle
\mathrm{BDC}, expliquer pourquoi on a
2 \times \widehat{\mathrm{ADC}}+2 \times \widehat{\mathrm{ADB}}=180^{\circ}.
3. En déduire que \widehat{\mathrm{ADC}}+\widehat{\mathrm{ADB}}=90^{\circ}.
4. En déduire la nature du triangle \mathrm{BCD}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Cet exercice a pour but de démontrer que le
point d'intersection des trois médiatrices du
triangle \mathrm{ABC} ci-dessous est le centre de son
cercle circonscrit.

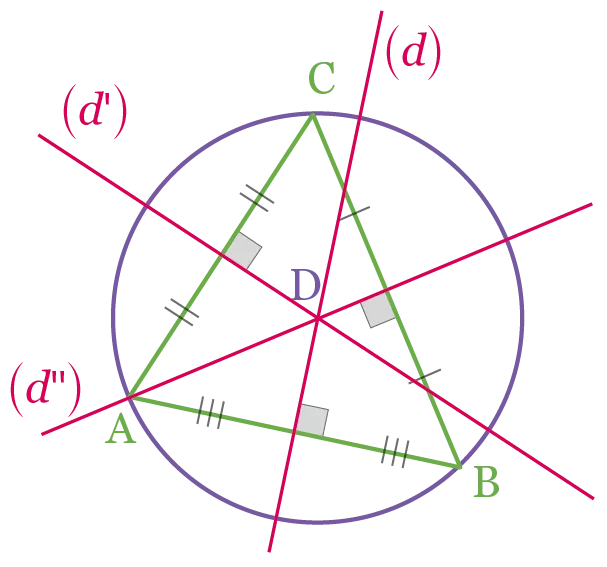


1. (d) est la médiatrice du segment [\mathrm{AB}].
Démontrer que \mathrm{DA}=\mathrm{DB}.
2. De même, \left(d^{\prime}\right) et \left(d^{\prime \prime}\right) sont les médiatrices
respectives des segments [\mathrm{AC}] et [\mathrm{CB}].
Démontrer que \mathrm{DA}=\mathrm{DB}=\mathrm{DC}.
3. En déduire que le point \mathrm{D} est le centre du
cercle circonscrit au triangle \mathrm{ABC}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Les points \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{F}, \mathrm{G} et \mathrm{H} appartiennent
tous au même cercle de centre \mathrm{I} de telle sorte que
\widehat{\mathrm{AIB}}=\widehat{\mathrm{BIC}}=\widehat{\mathrm{CID}}=\widehat{\mathrm{DIE}}=\widehat{\mathrm{EIF}}=\widehat{\mathrm{FIG}}=\widehat{\mathrm{GIH}}=\widehat{\mathrm{HIA}}.
Calculer la mesure de l'angle \widehat{\mathrm{GEB}}.

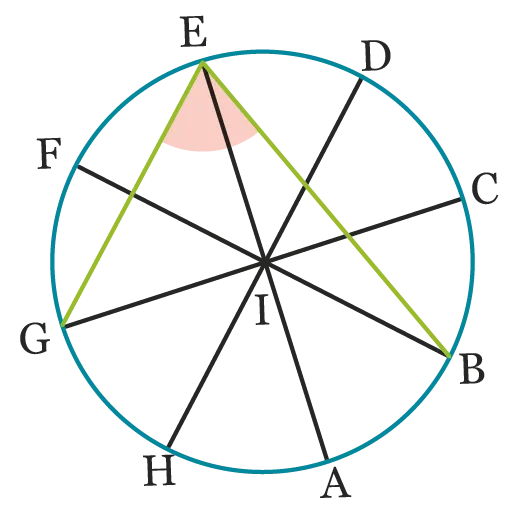
Calculer la mesure de l'angle \widehat{\mathrm{GEB}}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
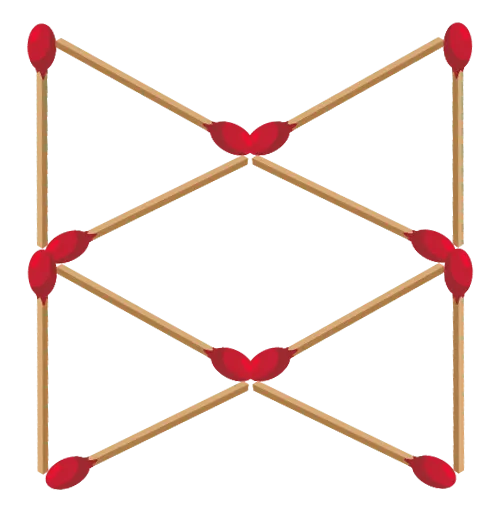
Comment obtenir
six triangles équilatéraux
de même taille en
déplaçant seulement
quatre allumettes ?



Cliquez ici pour avoir accès à un espace de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

