Chapitre 17
Savoir-faire
Aires et volumes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
MéthodeCalculer l'aire d'une surface
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Énoncé
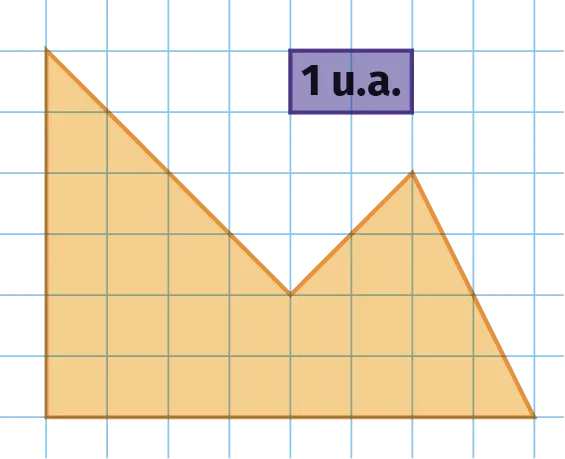
On considère la figure orange suivante.
1. Le rectangle violet définit l'unité d'aire (notée u.a.). Quelle est l'aire de la surface colorée en orange en u.a. ?
2. Chaque carré de la grille a pour côté 1~\mathrm{cm}. Quelle est l'aire de la surface orange en cm² ?
3. Convertir le résultat en dm².

Solution commentée
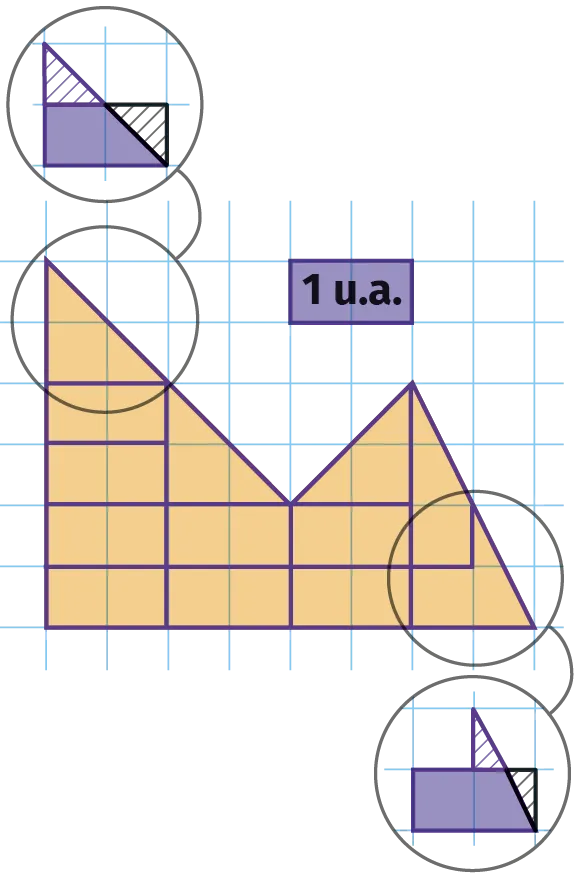
1. On doit compter le nombre de rectangles unités qui apparaissent ou que l'on peut reconstituer. Par exemple, les deux polygones entourés ont bien une aire égale au rectangle unité.
L'aire de la figure colorée en orange est 13 unités d'aire comme on le voit sur le quadrillage ci-contre.
2. On sait que 1~\mathrm{u.a.} = 2 carreaux =2 \times 1~\mathrm{cm}^2 = 2~\mathrm{cm}^2.
Puisque la surface colorée a une aire de 13~\mathrm{u.a.}, cela donne
13~\mathrm{u.a.} = 13 \times 2~ \mathrm{cm}^2 = 26~\mathrm{cm}^2.
3. 1~ \mathrm{dm}^2 = 100~ \mathrm{cm}^2,
donc 1~ \mathrm{cm}^2 = \frac{1}{100}~ \mathrm{dm}^2, donc
26~ \mathrm{cm}^2 = \frac{26}{100}~ \mathrm{dm}^2.26~ \mathrm{cm}^2 = 0,26~ \mathrm{dm}^2.

Supplément numérique
La méthode .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À mon tour
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Dans chaque cas, donner l'aire de
la figure orange.

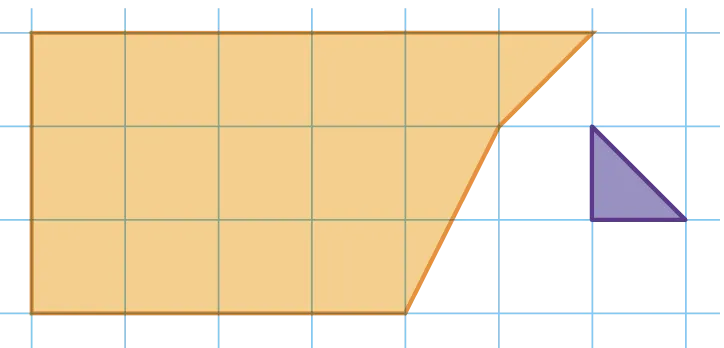
1. L'unité d'aire est un carré de la grille de côté 1~\mathrm{cm}.
2. L'unité d'aire est le triangle violet.


1. L'unité d'aire est un carré de la grille de côté 1~\mathrm{cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Dans chaque cas, donner l'aire de
la figure orange.

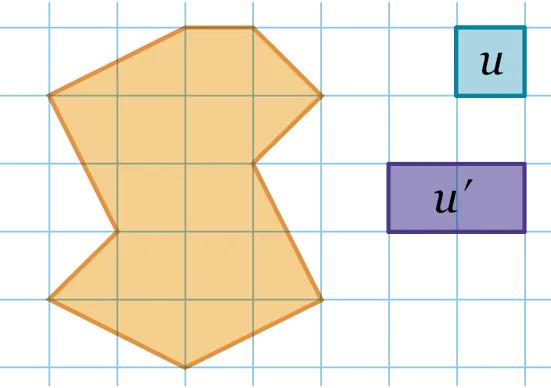
1. On prend u comme unité d'aire.
2. On prend u' comme unité d'aire.


1. On prend u comme unité d'aire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
MéthodeCalculer le volume d'un assemblage de cubes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Énoncé
On considère la figure suivante dont on donne deux vues
et on admet qu'elle n'est pas creuse.
Tous les cubes sont identiques et leur arête mesure 1~\mathrm{cm}.
Calculer le volume de cet assemblage.
Tous les cubes sont identiques et leur arête mesure 1~\mathrm{cm}.
Calculer le volume de cet assemblage.

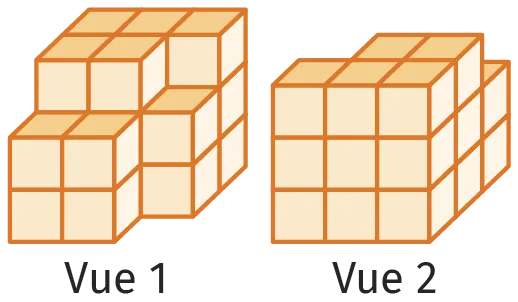
Solution commentée
- On commence par compter le nombre de cubes qui composent cet assemblage.

4+8+9=21. Cette figure est composée de 21 cubes. - Maintenant, on doit trouver quel est le volume d'un cube.
Ces cubes ont une arête mesurant 1~\mathrm{cm}, ils ont donc un volume de 1~\mathrm{cm}^3. - Il ne reste plus qu'à multiplier le volume d'un cube par le nombre total de cubes.
\mathcal{V}=21 \times 1=21. Cet assemblage a un volume de 21~\mathrm{cm}^3.
Supplément numérique
La méthode .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À mon tour
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour ces exercices, on considère que les
cubes ont des arêtes de longueur 1 cm et
que les assemblages ne sont pas creux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Compter le nombre
de cubes qui composent
l'assemblage suivant et en
déduire son volume.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
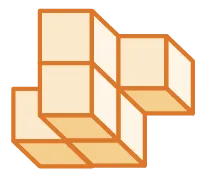
11
Compter le nombre
de cubes qui composent
l'assemblage suivant et en
déduire son volume.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
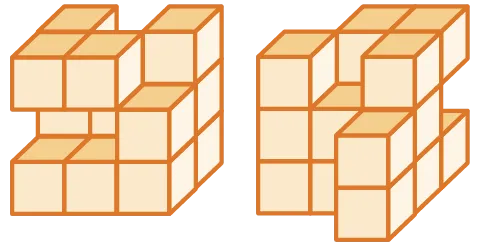
12
Calculer le volume de l'assemblage
suivant dont on donne deux vues.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
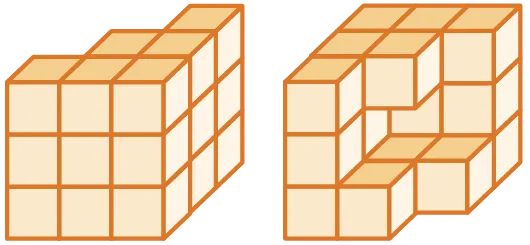
13
Calculer le volume de l'assemblage
suivant dont on donne deux vues.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


