Thème 1 : Nombres et calculs
Fiche 5
Étudier des problèmes algébriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
1. Utilisation d'un schéma en barres
Un schéma en barres modélise un problème en illustrant les différentes relations arithmétiques entre les données.On rencontre notamment les schémas en barres pour résoudre des problèmes additifs ou des problèmes multiplicatifs.
Exemples :
Schéma en barres pour un problème additif :

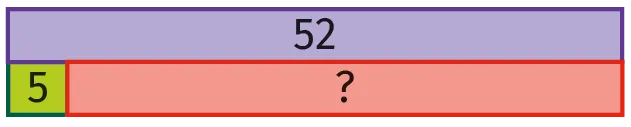
La valeur manquante est
52 - 5 = 47.


La valeur manquante est
52 - 5 = 47.
Schéma en barres pour un problème multiplicatif :

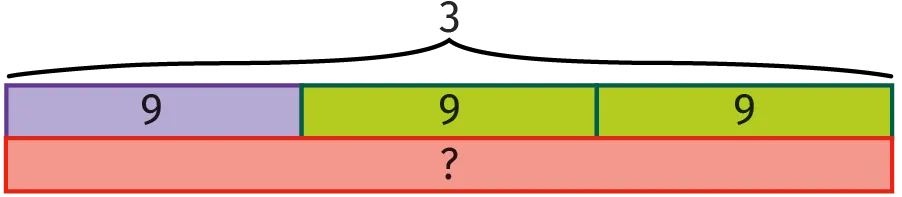
La valeur manquante est
3 \times 9=27.


La valeur manquante est
3 \times 9=27.
2. Résolution de problèmes utilisant des nombres inconnus
Lorsqu'une balance à plateaux est en équilibre, cela signifie que la masse de l'objet de gauche est égale à celle de l'objet de droite. On peut se servir de l'égalité pour déterminer la valeur d'un nombre inconnu.
Exemple : Ci-dessous, on a effectué trois pesées.





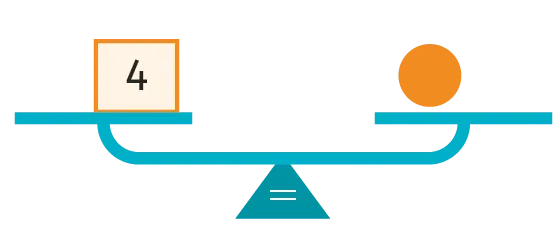


La croix verte est aussi
lourde que deux ronds
orange, d'où :
1 croix = 2 ronds.
1 croix = 2 ronds.


Le rond orange et 4 sont
aussi lourds que deux
ronds orange, d'où :
1 rond +~4 = 2 ronds.
1 rond +~4 = 2 ronds.


En retirant un rond de
chaque plateau, on obtient :
1 rond = 4, d'où :
1 croix = 2 ronds = 8.
1 croix = 2 ronds = 8.
Ce type de raisonnement reste valide lorsqu'on ne travaille pas sur des masses mais sur d'autres grandeurs telles que des prix.
3. Étude de motifs évolutifs
Certains motifs évolutifs admettent une structure qui se répète. On peut alors prévoir la forme du motif au bout de plusieurs répétitions. Lorsqu'on étudie un motif évolutif, on identifie particulièrement :- les quantités associées à la première étape ;
- la manière de passer d'une étape à la suivante.
Exemple :

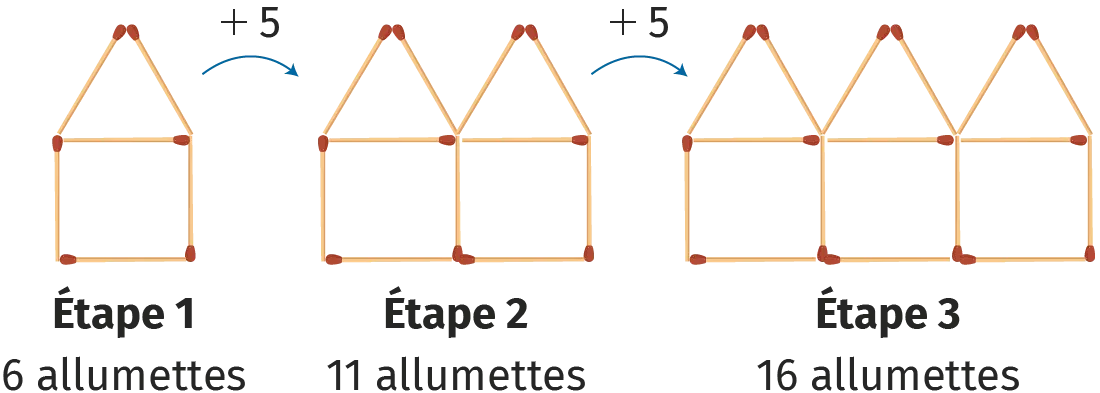
Ici, on compte 6 allumettes à la première étape et on en ajoute 5 à chaque étape. À l'étape 4, on a donc 6+(3 \times 5) allumettes, soit 21 allumettes.


Ici, on compte 6 allumettes à la première étape et on en ajoute 5 à chaque étape. À l'étape 4, on a donc 6+(3 \times 5) allumettes, soit 21 allumettes.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'utilisation des balances pour comparer des
masses date, au moins, de l'âge du bronze (de
2700 avant J.‑C. à 800 avant J.‑C.).
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 6 fois plus que 8 :
2. 28 \times 1 000 =
3. Indiquer 15 \text{ h } 20 sur l'horloge.
2. 28 \times 1 000 =
3. Indiquer 15 \text{ h } 20 sur l'horloge.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
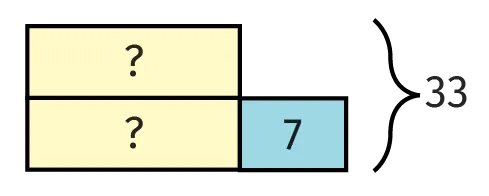
On a commencé à représenter différents
problèmes en utilisant des schémas en barres.
Achever la résolution en déterminant la valeur
manquante.







Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Exercice inversé
Exercice inversé
On a commencé à résoudre un
problème en utilisant un schéma en barres.
Écrire un énoncé possible qu'il peut illustrer.

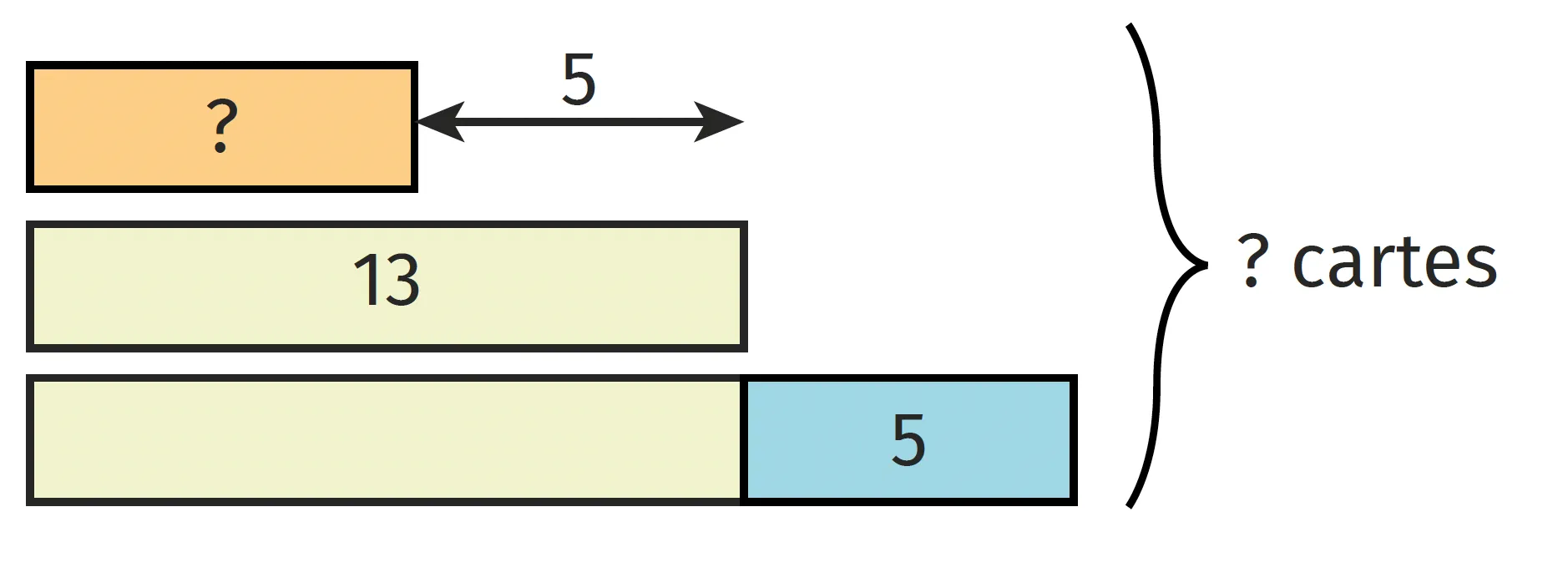
Écrire un énoncé possible qu'il peut illustrer.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Résoudre le problème en utilisant un schéma
en barres.
Dans un panier contenant des pommes et des poires, on compte 30 fruits au total et quatre fois plus de pommes que de poires. Combien y a-t-il de pommes et de poires dans ce panier ?
Dans un panier contenant des pommes et des poires, on compte 30 fruits au total et quatre fois plus de pommes que de poires. Combien y a-t-il de pommes et de poires dans ce panier ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Lors d'un concours culinaire, les trois meilleurs
cuisiniers seront récompensés en se partageant un
montant de 400~€.
Le premier gagnera 80~€ de plus que le second alors que le troisième gagnera 40~€ de moins que le second. À combien s'élèvera chacun des prix ?
Le premier gagnera 80~€ de plus que le second alors que le troisième gagnera 40~€ de moins que le second. À combien s'élèvera chacun des prix ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Copie d'élève
Copie d'élève
On donne ci-dessous une copie d'élève
répondant à l'exercice suivant.
Trouver la valeur d'une boule rouge.

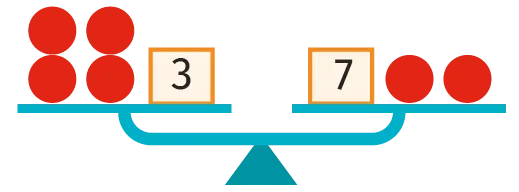

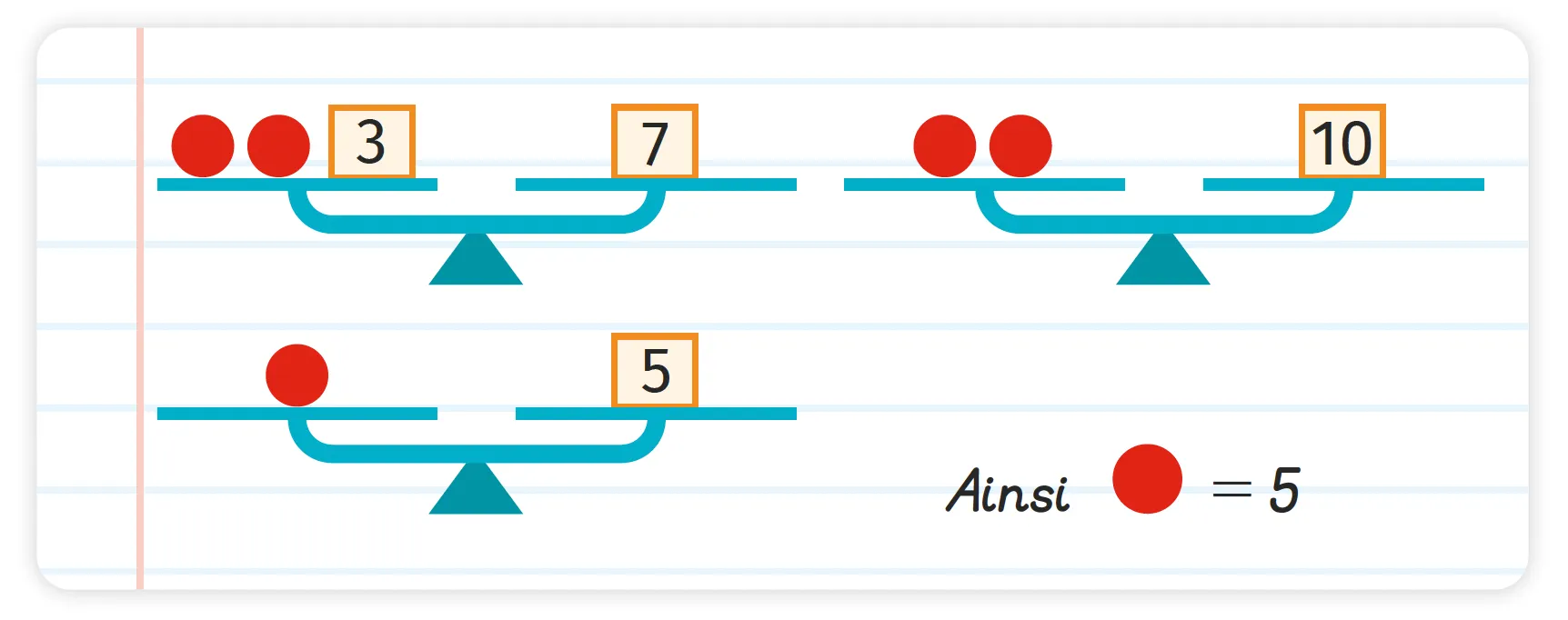
1. Comment vérifier que l'élève a fait une erreur ?
2. Trouver et corriger cette erreur, puis répondre
au problème initial
Trouver la valeur d'une boule rouge.




1. Comment vérifier que l'élève a fait une erreur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Déterminer la valeur d'une étoile.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Déterminer la valeur d'un rond et d'une étoile
à l'aide des informations suivantes.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
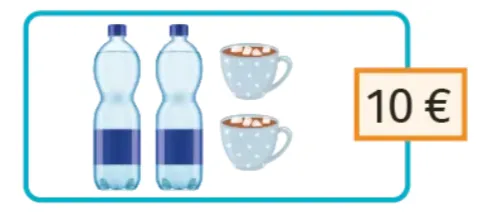
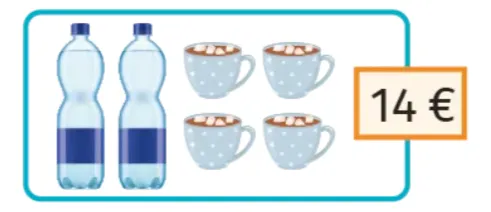
8
À l'aide des informations, déterminer le prix
d'une bouteille d'eau et le prix d'un chocolat chaud.






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
À l'aide des informations, déterminer le prix
d'un ananas et le prix d'une pastèque.








Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Avec des jetons identiques, on a construit le
modèle évolutif ci-dessous.
1. Dessiner le quatrième motif.
2. Calculer le nombre de jetons nécessaires à la construction :
a. du cinquième motif :
b. du dixième motif :
3. Calculer le nombre de jetons nécessaires à la
construction du centième motif.
1. Dessiner le quatrième motif.
2. Calculer le nombre de jetons nécessaires à la construction :
a. du cinquième motif :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
On donne ci-dessous un motif évolutif.
1. Représenter la première et la quatrième figure.
2. Donner le nombre de carreaux composant chacune des figures.
3. De combien de carreaux serait composée la sixième figure ?
1. Représenter la première et la quatrième figure.
2. Donner le nombre de carreaux composant chacune des figures.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
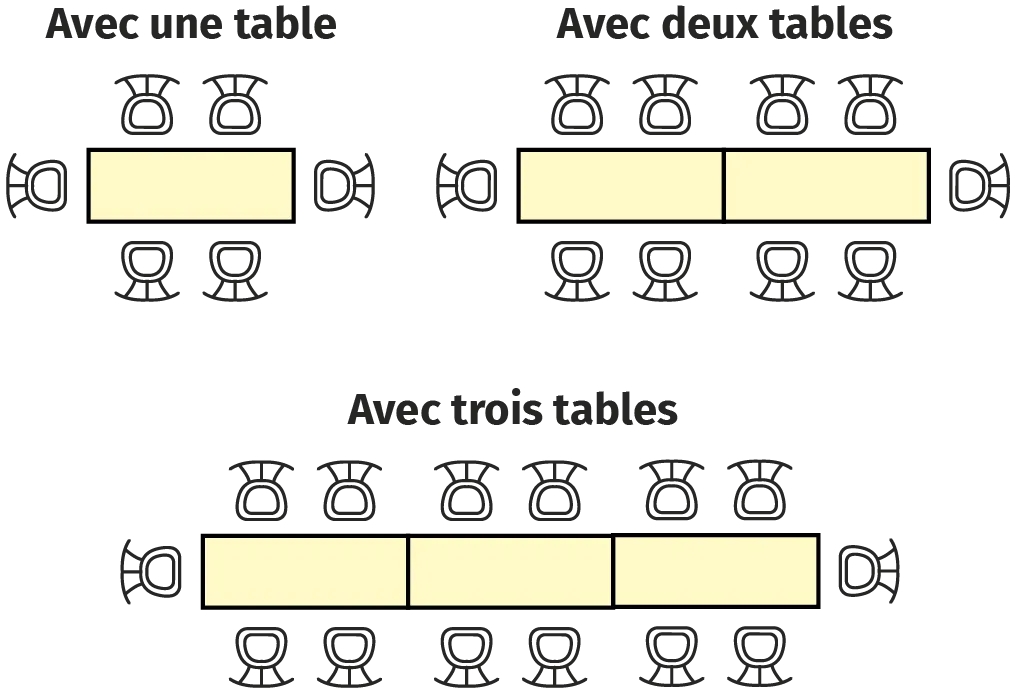
12
Une restauratrice organise des réceptions.
Selon le nombre de convives, elle dispose ses
tables rectangulaires en les accolant bout à bout.
Voici trois dispositions possibles.



La restauratrice ne dispose que de 50 tables.
1. Peut-elle accueillir 50 personnes en accollant dix tables bout à bout ?
2. Combien de personnes la restauratrice peut-elle
accueillir au maximum en accolant les tables bout
à bout ? Justifier.
1. Peut-elle accueillir 50 personnes en accollant dix tables bout à bout ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Énigme
On dispose de 8 pièces de monnaie qui
semblent identiques, mais l'une d'elles est
fausse et pèse légèrement plus lourd que les
autres. On dispose d'une balance à plateaux.
En utilisant la balance au maximum deux fois,
comment identifier la pièce différente ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

