Thème 1 : Nombres et calculs
Fiche 10
Additionner et soustraire des fractions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Propriété
Si deux fractions ont le même dénominateur, on peut les additionner (ou les soustraire) en additionnant (ou en soustrayant) les numérateurs et en conservant le dénominateur commun.
Exemple :
\frac{7}{4} + \frac{14}{4} = \frac{7+14}{4} = \frac{21}{4}
- Remarque : Pour additionner ou soustraire des fractions de dénominateurs différents, on les exprime d'abord avec le même dénominateur, puis on applique la propriété précédente.
Exemple :
On veut calculer \frac{5}{6} + \frac{1}{4}.
On doit donc modifier l'écriture des fractions de manière à avoir un dénominateur commun. On cherche un nombre qui soit à la fois dans la table de 6 et dans celle de 4. On trouve par exemple 12.
Ainsi, \frac{5}{6} + \frac{1}{4} = \frac{5 \times 2}{6 \times 2} + \frac{1 \times 3}{4 \times 3} = \frac{10}{12} + \frac{3}{12} = \frac{10+3}{12} = \frac{13}{12}.
On doit donc modifier l'écriture des fractions de manière à avoir un dénominateur commun. On cherche un nombre qui soit à la fois dans la table de 6 et dans celle de 4. On trouve par exemple 12.
Ainsi, \frac{5}{6} + \frac{1}{4} = \frac{5 \times 2}{6 \times 2} + \frac{1 \times 3}{4 \times 3} = \frac{10}{12} + \frac{3}{12} = \frac{10+3}{12} = \frac{13}{12}.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans les pays anglo-saxons, une fraction
dont le numérateur est supérieur ou égal
au dénominateur est appelée une fraction
impropre (improper fraction).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Entourer en rouge les pyramides, en bleu les pavés droits, en noir les boules et en vert les cylindres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Effectuer les calculs suivants.
1. \frac{11}{2} + \frac{17}{2} =
2. \frac{15}{4} - \frac{9}{4} =
2. \frac{15}{4} - \frac{9}{4} =
3. \left( \frac{54}{31} - \frac{31}{31} \right) + \frac{23}{31} =
4. \frac{121}{56} + \frac{25}{56} + \frac{1}{56} + \frac{26}{56} =
4. \frac{121}{56} + \frac{25}{56} + \frac{1}{56} + \frac{26}{56} =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Recopier et effectuer les calculs suivants.
1. \mathrm{A} =\frac{11}{2}+\frac{1}{6}
=\frac{11 \times \ldots}{2 \times \ldots}+\frac{1}{6}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
2. \mathrm{B} =\frac{15}{4}-\frac{1}{12}
=\frac{15 \times \ldots}{4 \times \ldots}-\frac{1}{12}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{11 \times \ldots}{2 \times \ldots}+\frac{1}{6}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{15 \times \ldots}{4 \times \ldots}-\frac{1}{12}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
3. \mathrm{C} =\frac{5}{14}+\frac{3}{2}
=\frac{5}{14}+\frac{\ldots \times \ldots }{\ldots \times \ldots}
=\frac{\ldots}{\ldots}+\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
4. \mathrm{D} =\frac{11}{12}-\frac{1}{3}
=\frac{\ldots}{\ldots}-\frac{\ldots\times\ldots}{\ldots\times\ldots}
=\frac{\ldots}{\ldots} - \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{5}{14}+\frac{\ldots \times \ldots }{\ldots \times \ldots}
=\frac{\ldots}{\ldots}+\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}-\frac{\ldots\times\ldots}{\ldots\times\ldots}
=\frac{\ldots}{\ldots} - \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Dans chacun des cas suivants, trouver
un dénominateur commun possible aux deux
fractions.
1. \frac{3}{8}
et
\frac{5}{12} :
2. \frac{3}{10} et \frac{7}{15} :
2. \frac{3}{10} et \frac{7}{15} :
3. \frac{5}{6}
et
\frac{3}{10} :
4. \frac{7}{12} et \frac{1}{9} :
4. \frac{7}{12} et \frac{1}{9} :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Recopier et effectuer les calculs suivants.
1. \mathrm{A} = \frac{11}{8} + \frac{1}{6}
= \frac{11 \times \ldots}{8 \times \ldots} + \frac{1 \times \ldots}{6 \times \ldots}
= \frac{\ldots}{24} + \frac{\ldots}{24}
=\frac{\ldots}{\ldots}
2. \mathrm{B} = \frac{3}{5} - \frac{1}{8}
= \frac{3 \times \ldots}{5 \times \ldots} - \frac{1 \times \ldots}{8 \times \ldots}
= \frac{\ldots}{40} - \frac{\ldots}{40}
=\frac{\ldots}{\ldots}
= \frac{11 \times \ldots}{8 \times \ldots} + \frac{1 \times \ldots}{6 \times \ldots}
= \frac{\ldots}{24} + \frac{\ldots}{24}
=\frac{\ldots}{\ldots}
= \frac{3 \times \ldots}{5 \times \ldots} - \frac{1 \times \ldots}{8 \times \ldots}
= \frac{\ldots}{40} - \frac{\ldots}{40}
=\frac{\ldots}{\ldots}
3. \mathrm{C} = \frac{1}{4} + \frac{5}{6}
= \frac{1 \times \ldots}{4 \times \ldots} + \frac{5 \times \ldots}{6 \times \ldots}
= \frac{\ldots}{12} + \frac{\ldots}{12}
=\frac{\ldots}{\ldots}
4. \mathrm{D} = \frac{8}{9} - \frac{5}{12}
= \frac{8 \times \ldots}{9 \times \ldots} - \frac{5 \times \ldots}{12 \times \ldots}
= \frac{\ldots}{36} - \frac{\ldots}{36}
=\frac{\ldots}{\ldots}
= \frac{1 \times \ldots}{4 \times \ldots} + \frac{5 \times \ldots}{6 \times \ldots}
= \frac{\ldots}{12} + \frac{\ldots}{12}
=\frac{\ldots}{\ldots}
= \frac{8 \times \ldots}{9 \times \ldots} - \frac{5 \times \ldots}{12 \times \ldots}
= \frac{\ldots}{36} - \frac{\ldots}{36}
=\frac{\ldots}{\ldots}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Recopier et effectuer les calculs suivants.
1. \mathrm{A} = \frac{5}{8} + \frac{7}{12}
= \frac{\ldots \times \ldots}{\ldots \times \ldots} + \frac{\ldots \times \ldots}{\ldots \times \ldots}
= \frac{\ldots}{\ldots} + \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
= \frac{\ldots \times \ldots}{\ldots \times \ldots} + \frac{\ldots \times \ldots}{\ldots \times \ldots}
= \frac{\ldots}{\ldots} + \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
2. \mathrm{B} = \frac{13}{20} + \frac{11}{15}
= \frac{\ldots \times \ldots}{\ldots \times \ldots} + \frac{\ldots \times \ldots}{\ldots \times \ldots}
= \frac{\ldots}{\ldots} + \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
= \frac{\ldots \times \ldots}{\ldots \times \ldots} + \frac{\ldots \times \ldots}{\ldots \times \ldots}
= \frac{\ldots}{\ldots} + \frac{\ldots}{\ldots}
=\frac{\ldots}{\ldots}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Selon la légende, Horus, dieu faucon, eut son œil coupé en six morceaux lors d'un combat face à Seth, chacun de ces morceaux représentant l'une des fractions
\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32} et \frac{1}{64}.

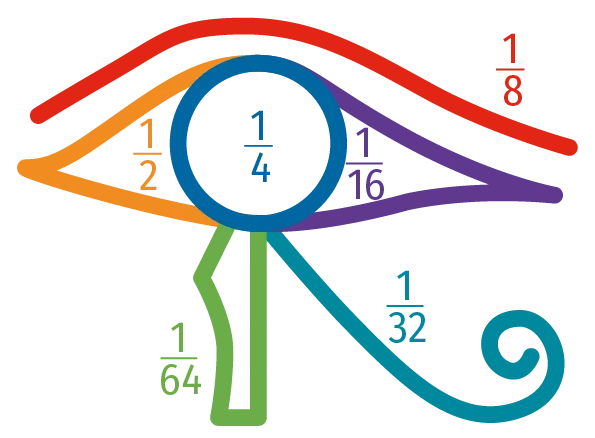


1. Montrer que l'œil d'Horus n'est pas complet.
2. La quantité manquante correspond, dans la légende, au liant magique permettant à l'œil de fonctionner à nouveau. À quelle fraction correspond ce liant magique ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Marion a mangé \frac{3}{8} d'un gâteau et Céleste en a mangé \frac{1}{6}.
1. Quelle fraction du gâteau a été mangée ?
2. Quelle fraction du gâteau reste-t-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Énigme
Trouver la valeur de \mathrm{?} dans l'égalité suivante.
\frac{17}{20} = \frac{3}{2} + \frac{1}{4} + \frac{1}{3} - \frac{5}{6} - \frac{2}{?}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

