Thème 1 : Nombres et calculs
Fiche 16
Multiplier des nombres décimaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouver une activité de découverte .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Propriétés
Multiplier un nombre par 10, c'est le rendre 10 fois plus grand.
Multiplier un nombre par 100, c'est le rendre 100 fois plus grand.
Multiplier un nombre par 0,1, c'est le rendre 10 fois plus petit.
Multiplier un nombre par 0,01, c'est le rendre 100 fois plus petit.
Multiplier un nombre par 0,001, c'est le rendre 1~000 fois plus petit.
- Remarque : Il est possible de calculer astucieusement certains produits.
Exemples :
- 7 \times {\color{red}0,04} = 7 \times {\color{red}4 \times 0,01} = 28 \times 0,01 = 0,28
- {\color{blue}0,6} \times {\color{red}1,2} = {\color{blue}0,1 \times 6} \times {\color{red}12 \times 0,1} = 0,1 \times 72 \times 0,1 = 7,2 \times 0,1 = 0,72
Méthode
Dans le cadre d'un produit quelconque de décimaux, on pose l'opération.
1. On remarque que : 126,93 = 12~693 \times 0,01 et 4,5 = 45 \times 0,1.
2. On calcule le produit 12~693 \times 45 = 571~185.
3. On observe que 0,01 \times 0,1 = 0,001.
4. On conclut : 126,93 \times 4,5 = 571~185 \times 0,001 = 571,185.
2. On calcule le produit 12~693 \times 45 = 571~185.
3. On observe que 0,01 \times 0,1 = 0,001.
4. On conclut : 126,93 \times 4,5 = 571~185 \times 0,001 = 571,185.
\begin{array}{r}
12~693 \\
\times \quad 45 \\
\hline
63~465 \\
+~507~720 \\
\hline
571~185
\end{array}
- Remarque : Pour vérifier le résultat, on peut utiliser les ordres de grandeur.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Multiplier une vitesse donnée en \mathrm{m/s} par 3,6
permet de la convertir en \mathrm{km/h}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parmi les trois triangles, un est isocèle, un est équilatéral et un est rectangle. Coder les figures.



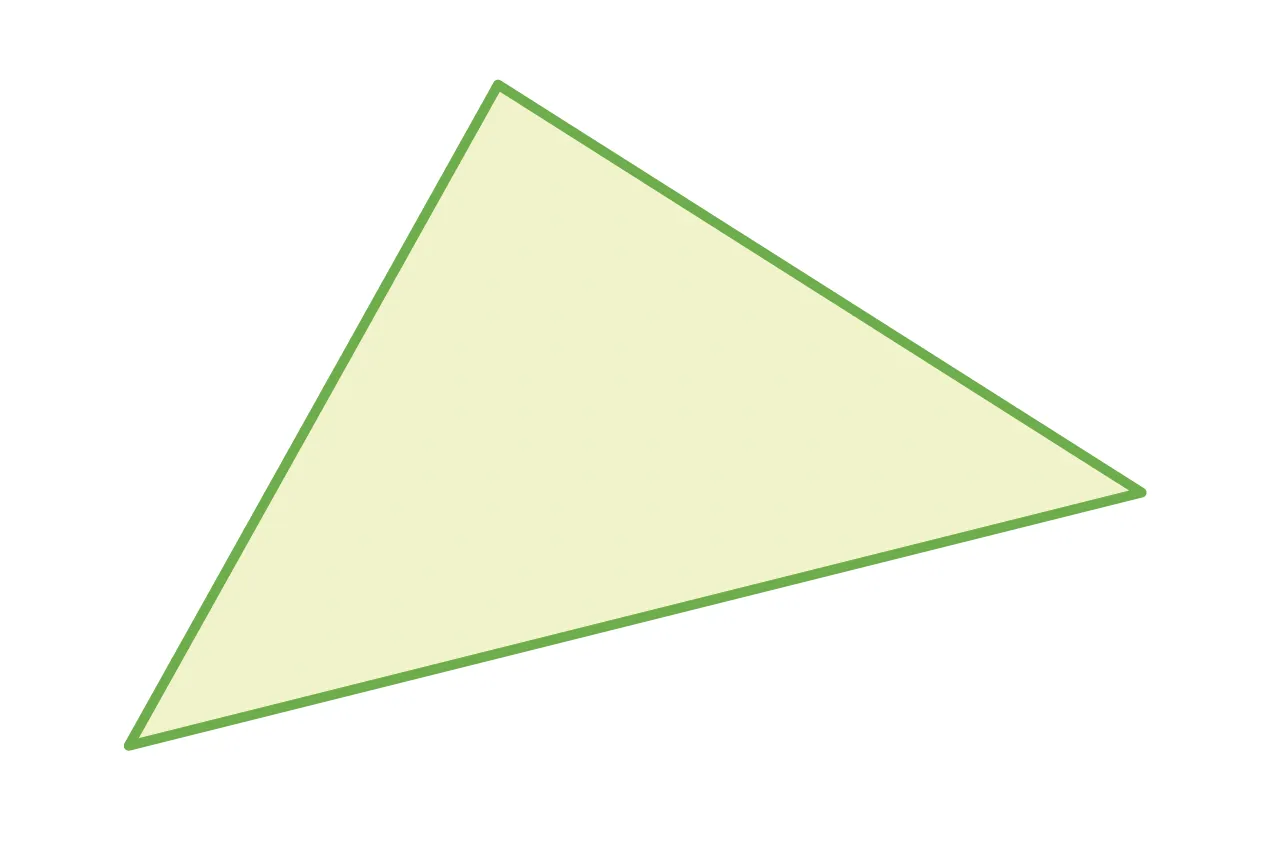

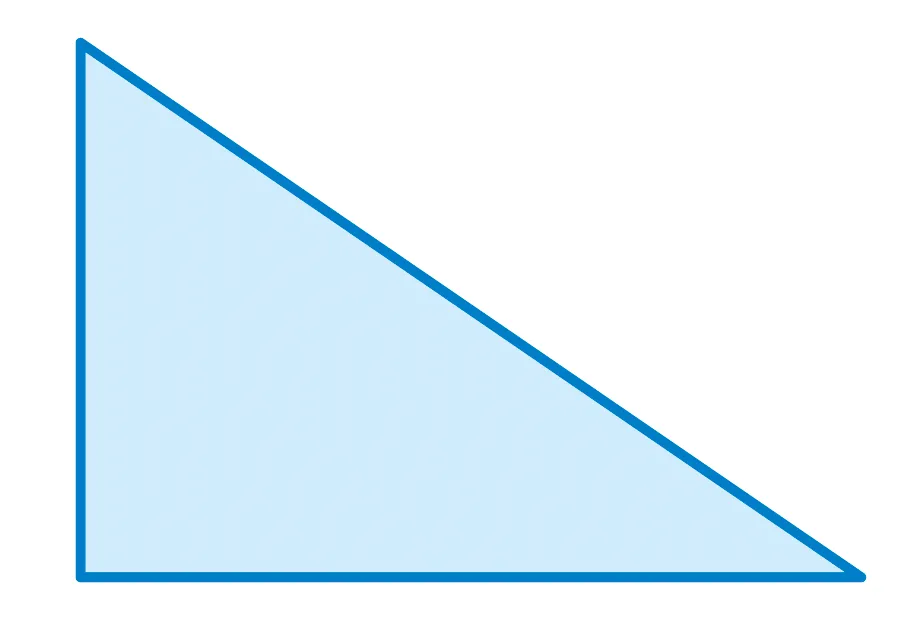






Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Compléter les égalités ci-dessous.
1. 14,5 \times 10 =
2. 10 \times 63,47 =
3. 6,987 \times 100 =
4. 100 \times 78,4 =
5. 4,4 \times 0,1 =
1. 14,5 \times 10 =
2. 10 \times 63,47 =
3. 6,987 \times 100 =
4. 100 \times 78,4 =
5. 4,4 \times 0,1 =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Compléter les égalités ci-dessous.
1. 0,01 \times 53,7 =
2. 0,1 \times 3~421 =
3. 76,35 \times 0,001 =
4. 0,1 \times 0,01 =
1. 0,01 \times 53,7 =
2. 0,1 \times 3~421 =
3. 76,35 \times 0,001 =
4. 0,1 \times 0,01 =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Compléter les pointillés ci-dessous pour que les égalités soient vraies.
1. 13,2 \times = 1~320
2. 895,36 \times = 89,536
3. 750,213 \times = 75~021,3
4. 0,001 \times = 3~734
5. 3,45 \times = 0,345
1. 13,2 \times
2. 895,36 \times
3. 750,213 \times
4. 0,001 \times
5. 3,45 \times
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Compléter les pointillés ci-dessous pour que les égalités soient vraies.
1. \times 1~000 = 563~563,1
2. \times 54,37 = 5~437
3. \times 0,1 = 121
4. \times 100 = 3,14
5. \times 1~000 = 1,4
1.
2.
3.
4.
5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Compléter les égalités ci-dessous.
1. 1,2 \times 0,4 = 12 \times \times 4 \times =
2. 200 \times 0,6 =
3. 2,1 \times 0,02 =
4. 0,03 \times 2,5 =
1. 1,2 \times 0,4 = 12 \times
2. 200 \times 0,6 =
3. 2,1 \times 0,02 =
4. 0,03 \times 2,5 =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Compléter les égalités ci-dessous.
1. 0,6 \times 1,1 =
2. 30 \times 0,12 =
3. 32 \times 0,003 =
4. 3,1 \times 0,05 =
1. 0,6 \times 1,1 =
2. 30 \times 0,12 =
3. 32 \times 0,003 =
4. 3,1 \times 0,05 =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Sachant que 132 \times 35 = 4~620 et sans faire aucun autre calcul, résoudre les problèmes suivants.
1. Un magasin a vendu 35 t-shirts à 13,20~\euro l'unité. Quel est le montant total de la vente ?
2. Une école a acheté 1~320 bureaux à 35~\euro l'unité. À combien s'élève la facture ?
3. Nour a acheté 3,5~\text{kg} de bananes à 1,32~\euro\text{/kg}. Quel montant a-t-elle payé ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Copie d'élève
Copie d'élève
Voici quatre multiplications effectuées par des élèves toutes incorrectes.
Proposer une correction de chacune d'elles.
Proposer une correction de chacune d'elles.
\begin{array}{r}
75,2 \\
\times \quad 3,5 \\
\hline 3~760 \\
+\quad 2~256 \\
\hline 60,16
\end{array}
\begin{array}{r}
35,1 \\
\times \quad 3,2 \\
\hline 702 \\
+10~530 \\
\hline 1~123,2
\end{array}
\begin{array}{r}
4,1 \\
\times \quad 32,4 \\
\hline 164 \\
820 \\
+\quad 1~230 \\
\hline 22,14
\end{array}
\begin{array}{r}
7,5 \\
\times \quad 8,9 \\
\hline 725 \\
+\quad 5~600 \\
\hline 53,25
\end{array}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Poser et effectuer les multiplications suivantes.
1. 1,4 \times 2,1
2. 31,2 \times 5,12
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Poser et effectuer les multiplications suivantes.
3. Contrôler les résultats obtenus en utilisant un ordre de grandeur.
21,3 \times 1,98 \approx
64,39 \times 4,54 \approx
1. 21,3 \times 1,98
2. 64,39 \times 4,54
3. Contrôler les résultats obtenus en utilisant un ordre de grandeur.
21,3 \times 1,98 \approx
64,39 \times 4,54 \approx
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
On achète des pommes de terre au supermarché.


Compléter le prix indiqué sur la balance.


Compléter le prix indiqué sur la balance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Les parents d'Enzo lui ont acheté une loupe qui grossit de 3,5 fois ce qui est observé. Il observe une coccinelle posée sur son bureau qui mesure en réalité 0,8~\mathrm{cm} de long.
Quelle sera la taille apparente de la coccinelle lorsqu'il l'observera à l'aide de la loupe ?
Quelle sera la taille apparente de la coccinelle lorsqu'il l'observera à l'aide de la loupe ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
Antoine et Kylian ont tous les deux participé à une course à pied. À l'arrivée, la montre d'Antoine indique qu'il a couru à 11,7~\mathrm{km/h} et celle de Kylian indique qu'il a couru à 3,25~\mathrm{m/s}.
Qui a couru le plus vite ?
Coup de pouce
on pourra utiliser l'anecdote de cette fiche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
Un parking propose la formule suivante : on paie proportionnellement au temps passé au tarif de 0,60~\euro chaque heure. Elena reste stationnée 1 heure et demi dans ce parking.
Quel prix va-t-elle payer ?
Quel prix va-t-elle payer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
Une compagnie aérienne n'autorise pas les bagages pesant plus de 10~\mathrm{kg}. Elle facture tout supplément au tarif de 10,50~€ par \mathrm{kg} dépassé.
La valise de Léana pèse 11,2~\mathrm{kg}.
Combien va-t-elle payer ?
La valise de Léana pèse 11,2~\mathrm{kg}.
Combien va-t-elle payer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Le kilowattheure (kWh) est une unité mesurant l'énergie consommée par un appareil électrique. En France, en 2025, le prix du kWh est estimé à près de 0,21~€. On considère une télévision qui, en un an, consomme 205,2~\mathrm{kWh}.
Estimer le coût de l'électricité consommée, en un an, par cette télévision.
Estimer le coût de l'électricité consommée, en un an, par cette télévision.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Énigme
Les figures suivantes sont composées de rectangles. Déterminer les longueurs ou les aires manquantes.
Attention les figures ne sont pas aux bonnes dimensions.

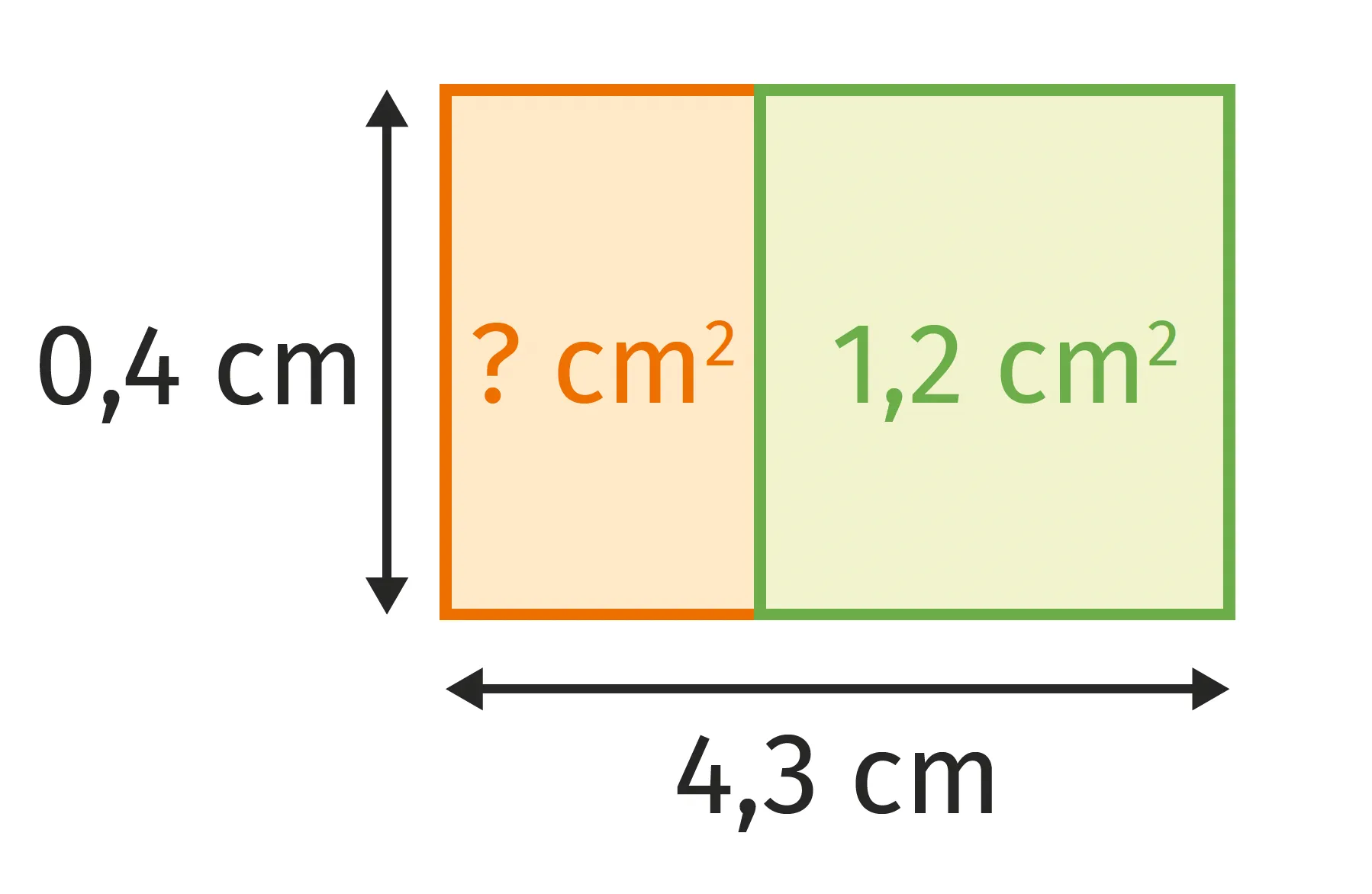

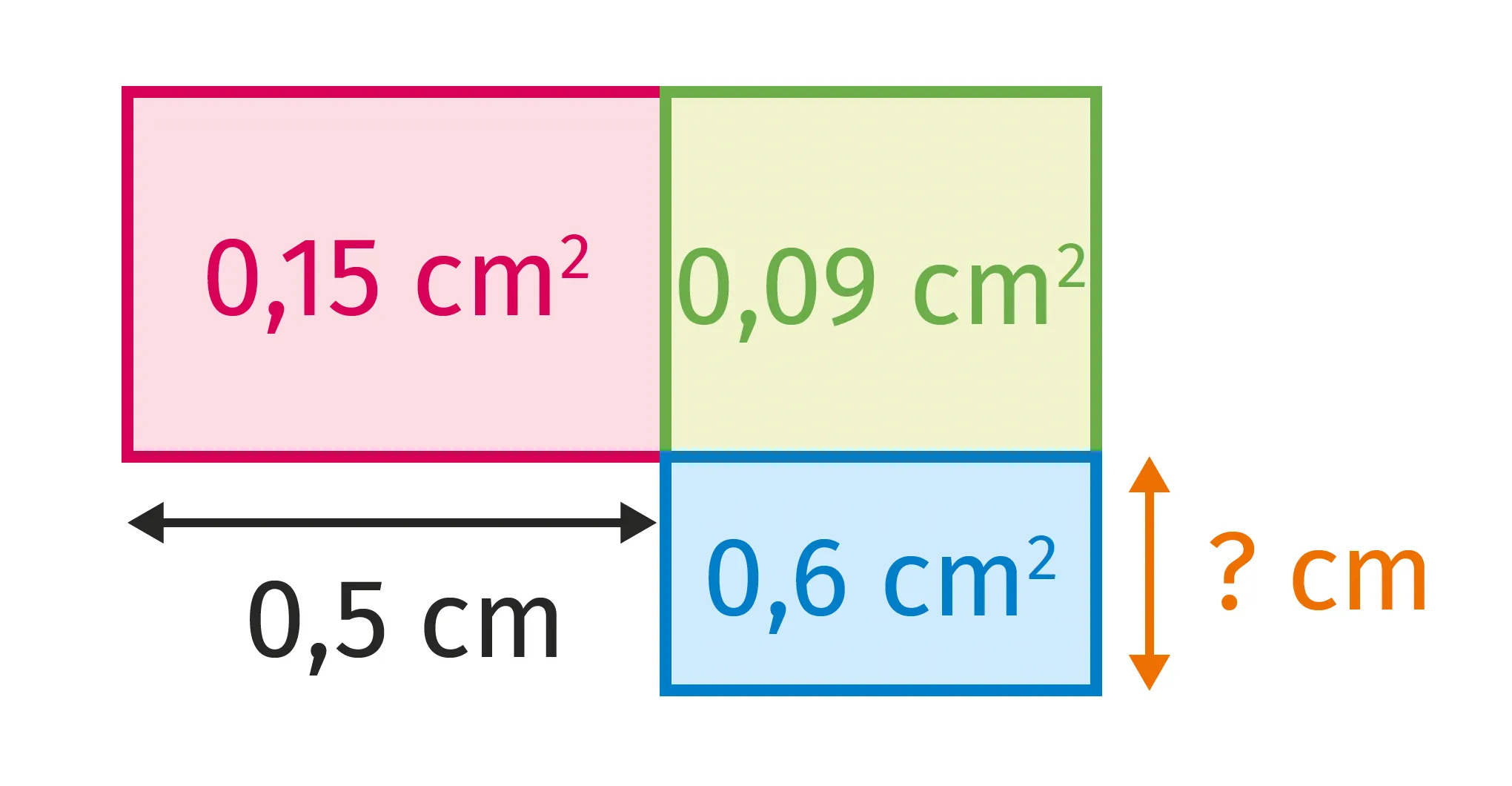
Attention les figures ne sont pas aux bonnes dimensions.
Coup de pouce
\text{Aire(rectangle)} = \text{longueur} × \text{largeur}


\text{?} = \text{cm²}


\text{?} = \text{cm}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


