Thème 1 : Nombres et calculs
Fiche 17
Effectuer une division décimale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définitions
Le quotient d'un nombre décimal a par un entier non nul b est le nombre qui, multiplié par b, donne a. Le quotient est donc le nombre qui permet de compléter l'égalité : b \times \ldots = a.
Effectuer la division décimale de a par b, c'est trouver une valeur (exacte ou approchée) de ce quotient.
Méthode
Pour poser une division décimale, on applique la même procédure que celle utilisée pour poser une division euclidienne, mais en continuant si nécessaire à « descendre » les 0.
L'algorithme s'arrête si on a baissé tous les chiffres du dividende (et éventuellement des 0 supplémentaires) et que le reste obtenu est nul. Sinon, l'algorithme ne s'arrête pas.
Exemple : Effectuons la division décimale de 265,42 par 5.


L'algorithme de division décimale s'arrête : on a donc 265,42 \div 5 = 53,084.


L'algorithme de division décimale s'arrête : on a donc 265,42 \div 5 = 53,084.
Propriétés
On considère deux entiers a et b, avec b \neq 0.
• Si l'algorithme de division décimale de a par b s'arrête, alors la fraction \frac{a}{b} est un nombre décimal.
• Si l'algorithme de division décimale de a par b ne s'arrête jamais, alors la fraction \frac{a}{b} n'est pas un nombre décimal.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans les pays anglo-saxons, on utilise le point
plutôt que la virgule pour écrire les nombres
décimaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 3 + 2 \times 1~000 + 3 \times \frac{1}{100} =
2. Le triple de 9 :
3. \frac{1}{3} de 6 mètres :
2. Le triple de 9 :
3. \frac{1}{3} de 6 mètres :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Compléter les égalités ci-dessous.
1. 172,3 \div 100 =
2. 73~590 \div 1~000 =
3. 7,05 \div 10 =
2. 73~590 \div 1~000 =
3. 7,05 \div 10 =
4. 3~590 \div = 35,9
5. 9,3 \div = 0,009~3
5. 9,3 \div
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
1. Mettre la virgule au bon endroit dans chacun des quotients suivants.
2. Écrire les égalités obtenues.
× =
× =
2. Écrire les égalités obtenues.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
1. Compléter les divisions à trous suivantes.
2. Écrire les égalités obtenues.
× =
× =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
1. Compléter les divisions à trous suivantes sans oublier les virgules.
2. Écrire les égalités obtenues.
× =
× =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Poser et effectuer les divisions suivantes.
Arrondir au millième si besoin.
Arrondir au millième si besoin.
1. 32,7 ÷ 3 =
2. 252,35 ÷ 5 =
3. 38 ÷ 7 ≈
4. 7,25 ÷ 6 ≈
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Calculer, pour chacune des fractions, la valeur décimale exacte en posant la division décimale.
1. \frac{14}{8} =
2. \frac{7}{2} =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
1. Déterminer une valeur décimale approchée au millième de \frac{17}{9}.
2. Déterminer une valeur décimale approchée au millième de \frac{19}{6}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Sun a acheté 3~\mathrm{kg} de tomates pour 8,19~\euro. Quel est le prix au kilogramme de ces tomates ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Alban a acheté à la foire aux livres un livre de collection à 24~\euro et trois livres jeunesse, tous de même prix. Il a dépensé au total 31,05~\euro.
On cherche à connaître le prix d'un livre jeunesse.
1. Compléter le schéma en barres ci-dessous.
2. Répondre au problème posé.
On cherche à connaître le prix d'un livre jeunesse.
1. Compléter le schéma en barres ci-dessous.
2. Répondre au problème posé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
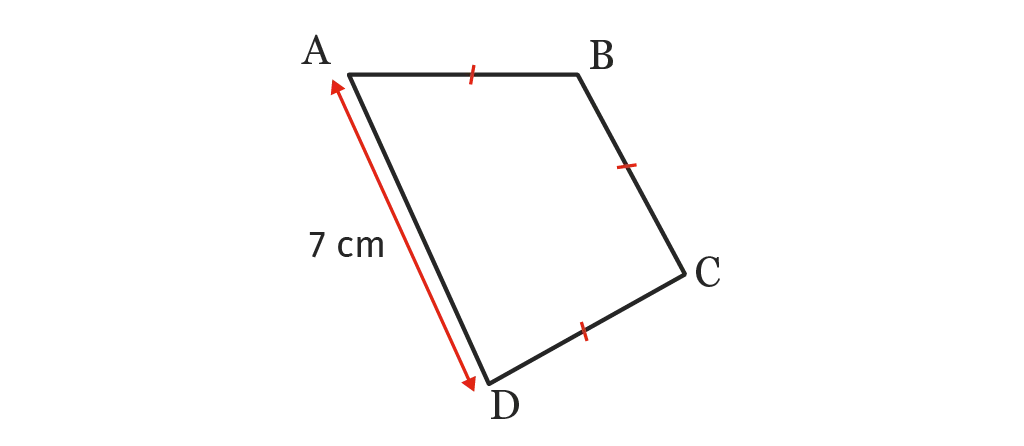
On donne la figure ci-dessous. Déterminer la longueur \text{AB} sachant que le périmètre de la figure vaut 19,75~\mathrm{cm}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
Maddy remplit 8 verres équitablement en utilisant une bouteille de 2~\mathrm{L}.
Combien de cL contient chaque verre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Compléter les graduations de chaque demi-droite graduée en effectuant les calculs nécessaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Énigme
Quelle est la 35^{\mathrm{e}} décimale de \frac{1}{7} ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


