Thème 1 : Nombres et calculs
Fiche 18
Comparer des nombres de différentes écritures
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Pour comparer deux nombres, il est souvent nécessaire de les écrire sous la même forme.
Il existe plusieurs méthodes pour comparer des fractions.
- Remarques :
1. Un nombre décimal se réécrit sous la forme d'une fraction : 4,251 = \frac{4~251}{1~000}.
2. Un pourcentage se réécrit sous la forme d'une fraction : 3~\% = \frac{3}{100}.
3. Un nombre mixte se réécrit sous la forme d'une fraction : 8+\frac{3}{7}=\frac{8 \times 7}{7}+\frac{3}{7}=\frac{56}{7}+\frac{3}{7}=\frac{59}{7}.
Méthode
Il existe plusieurs méthodes pour comparer des fractions.
- On peut aisément comparer deux fractions de même dénominateur ou deux fractions de même numérateur : \frac{2}{7} \lt \frac{5}{7} et \frac{2}{3} > \frac{2}{7}.
- On peut utiliser une comparaison à un même nombre : \frac{9}{7} > 1 et \frac{5}{6} \lt 1 donc \frac{9}{7} > \frac{5}{6}.
- On peut utiliser les nombres mixtes : \frac{51}{7}=7+\frac{2}{7} et \frac{38}{6}=6+\frac{2}{6} et 7 > 6 donc \frac{51}{7} > \frac{38}{6}.
- On peut calculer le quotient (exact ou arrondi) : \frac{37}{7} \approx 5,3 et \frac{72}{16} = 4,5 donc \frac{37}{7} > \frac{72}{16}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le symbole d'égalité = a été introduit par
Robert Recorde en 1557, plus de trois siècles
avant le symbole d'approximation \approx utilisé par
Anton Steinhauser en 1875.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. À quelle fraction de la figure correspond l'aire coloriée ?

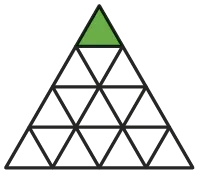


2. 100 \times \frac{1}{10}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Comparer les fractions suivantes.
1. \frac{5}{3} \frac{8}{3}
2. \frac{15}{4} \frac{7}{4}
3. \frac{25}{17} \frac{24}{17}
1. \frac{5}{3}
2. \frac{15}{4}
3. \frac{25}{17}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Comparer les fractions suivantes.
1.
\frac{5}{3} \frac{5}{14}
2.
\frac{9}{7} \frac{9}{11}
3.
\frac{17}{13} \frac{17}{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
1. Écrire ces fractions en utilisant 12 comme
dénominateur.
2. Ranger ces fractions dans l'ordre croissant
\frac{3}{2} = \frac{\ldots}{\ldots} = \frac{\ldots}{\ldots}
\frac{8}{3} = \frac{\ldots}{\ldots} = \frac{\ldots}{\ldots}
\frac{14}{24} = \frac{\ldots}{\ldots} = \frac{\ldots}{\ldots}
\frac{5}{4} = \frac{\ldots}{\ldots} = \frac{\ldots}{\ldots}
\frac{5}{6} = \frac{\ldots}{\ldots} = \frac{\ldots}{\ldots}
2. Ranger ces fractions dans l'ordre croissant
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
1. Entourer en rouge les nombres inférieurs à
1, les nombres supérieurs à 1 et les
nombres égaux à 1.
2.
Compléter en utilisant \lt ou >. Utiliser ? si la
question 1 ne permet pas de répondre.
3.
Utiliser une autre méthode pour les
comparaisons restantes.
\frac{2}{3} \frac{14}{6}
\frac{4}{7} \frac{11}{11}
\frac{14}{6} \frac{11}{11}
\frac{4}{7} \frac{11}{11}
\frac{14}{6} \frac{11}{11}
\frac{2}{3} \frac{4}{7}
\frac{11}{11} \frac{30}{25}
\frac{14}{6} \frac{30}{25}
\frac{11}{11} \frac{30}{25}
\frac{14}{6} \frac{30}{25}
\frac{14}{6} \frac{4}{7}
\frac{2}{3} \frac{30}{25}
\frac{2}{3} \frac{30}{25}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
1. En posant les divisions euclidiennes, écrire
sous forme de nombres mixtes les nombres suivants.
2. Utiliser ces écritures pour comparer ces deux
fractions.
a. \frac{61}{7}=
b. \frac{111}{11}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Copie d'élève
Copie d'élève
On a demandé à Nathan d'écrire le nombre
8,17 sous la forme d'une fraction. Voici sa réponse.
1. Comparer à 1 les nombres 8,17 et \frac{8}{17}.
2. Que peut-on en déduire ? Donner une réponse
possible à l'énoncé.
C'est \frac{8}{17}.
1. Comparer à 1 les nombres 8,17 et \frac{8}{17}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
1. Colorier de la même couleur les cases
contenant des nombres égaux.
2. Ranger dans l'ordre décroissant ces nombres.
2. Ranger dans l'ordre décroissant ces nombres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Aider le lutin à rejoindre sa maison le plus
rapidement possible. Il ne peut passer que sur des
cases voisines dont le nombre est supérieur ou
égal à celui de la case précédente.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Ranger les nombres suivants dans l'ordre
croissant.
8,4 \quad 86~\% \quad 8,18 \quad 8~+~\frac{4}{5}
\quad \frac{77}{9} \quad 8,5 \quad 8+\frac{3}{4}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Énigme
1. Trouver une fraction comprise entre \frac{1}{3} et \frac{1}{2}.
2. Trouver une fraction comprise entre \frac{1}{7} et \frac{1}{6}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


