Thème 2 : Grandeurs et mesures
Fiche 31
Calculer le volume d'un cube ou d'un assemblage de cubes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définition
Le volume d'un solide est une grandeur correspondant à la place qu'il occupe dans l'espace.
Définitions
Le centimètre cube, noté \mathrm{cm}^3, est une unité correspondant au volume d'un cube dont l'arête mesure 1~ \mathrm{cm}. Un tel cube est appelé cube unité.
Propriété
Le volume d'un solide est déterminé par le nombre de cubes unités qu'il peut contenir.
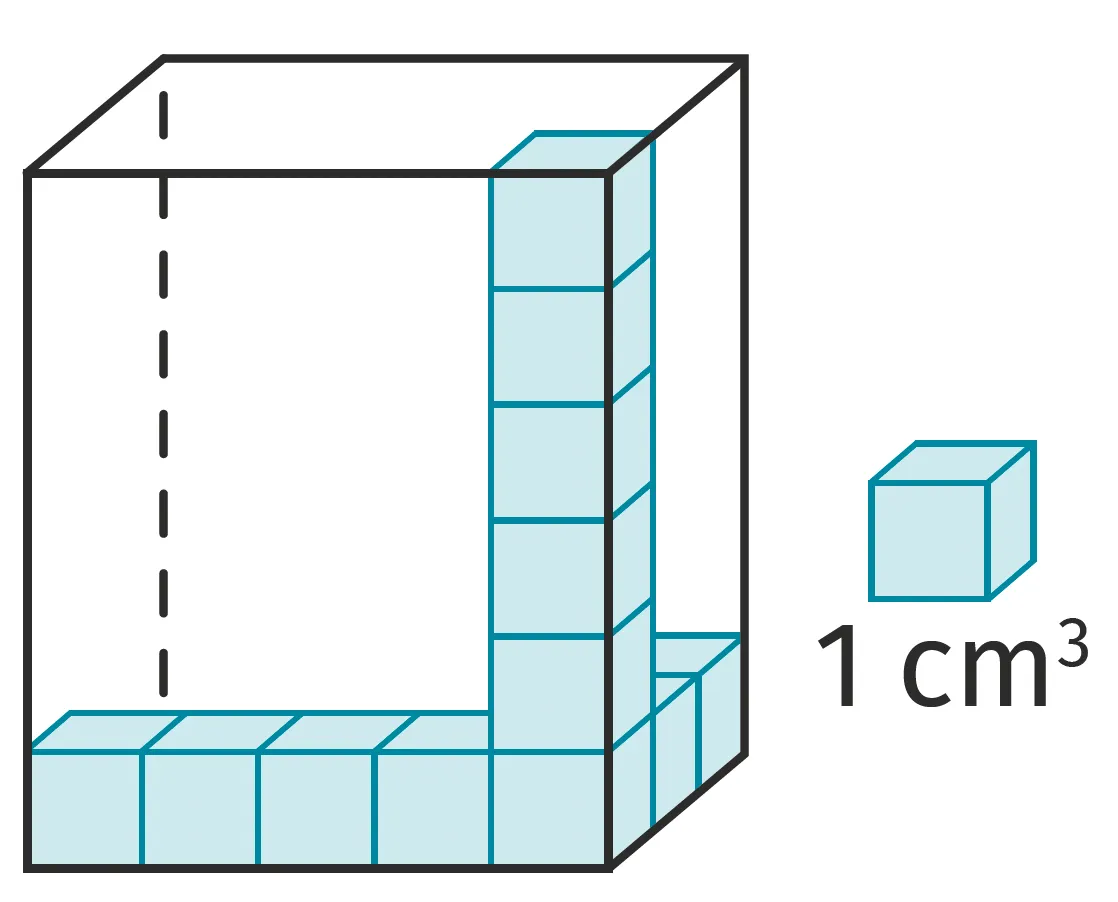
Exemple : Le solide représenté ici peut contenir 5 \times 6 \times 3 cubes unités. Son volume est donc de 5 \times 6 \times 3 = 90~ \mathrm{cm}^3.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une ruche standard a la forme d'un pavé droit
qui mesure 50 \text{ cm} de long, 43 \text{ cm} de large
et 32 \text{ cm} de haut et peut contenir jusqu'à
60~000 abeilles. Chaque abeille peut donc
théoriquement occuper un volume d'environ
1,145 \text{ cm}^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Quelle est l'heure indiquée sur cette horloge ?
2. Placer les aiguilles correspondant à 14 h 25.
3. 1+3 \times \frac{1}{10}+\frac{4}{100}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Déterminer le volume des pavés droits suivants.
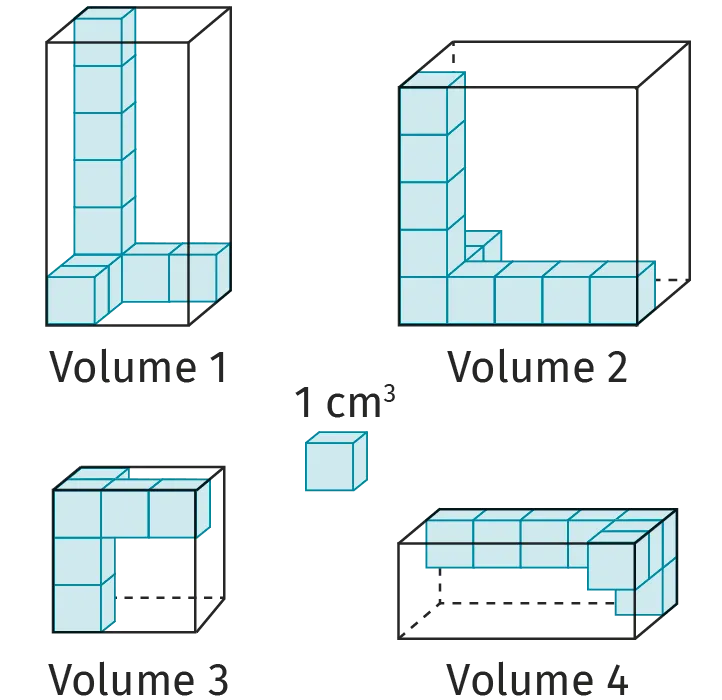
Volume 1 :
Volume 2 :
Volume 2 :
Volume 3 :
Volume 4 :
Volume 4 :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
1. Déterminer le nombre de cubes unité que peut contenir le solide ci-dessous.
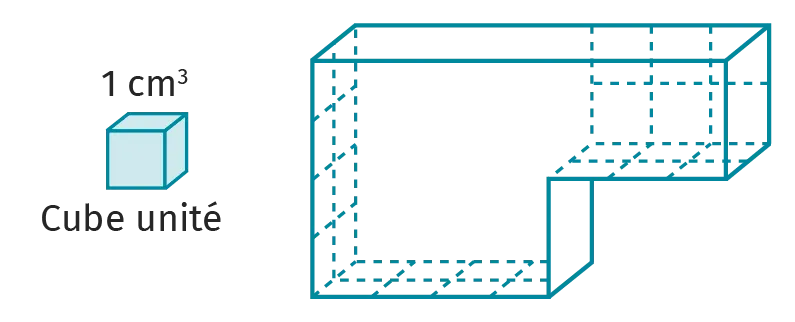2. En déduire le volume du solide en cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
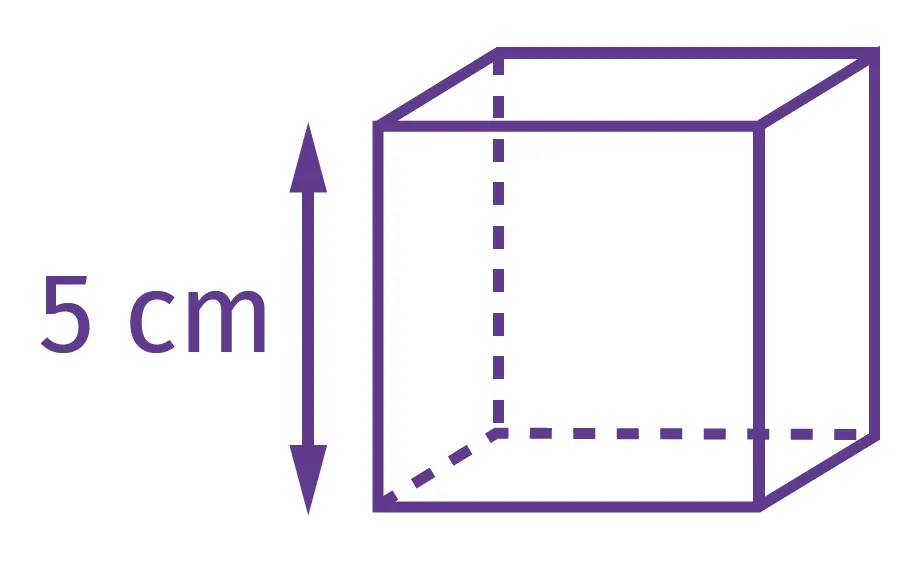
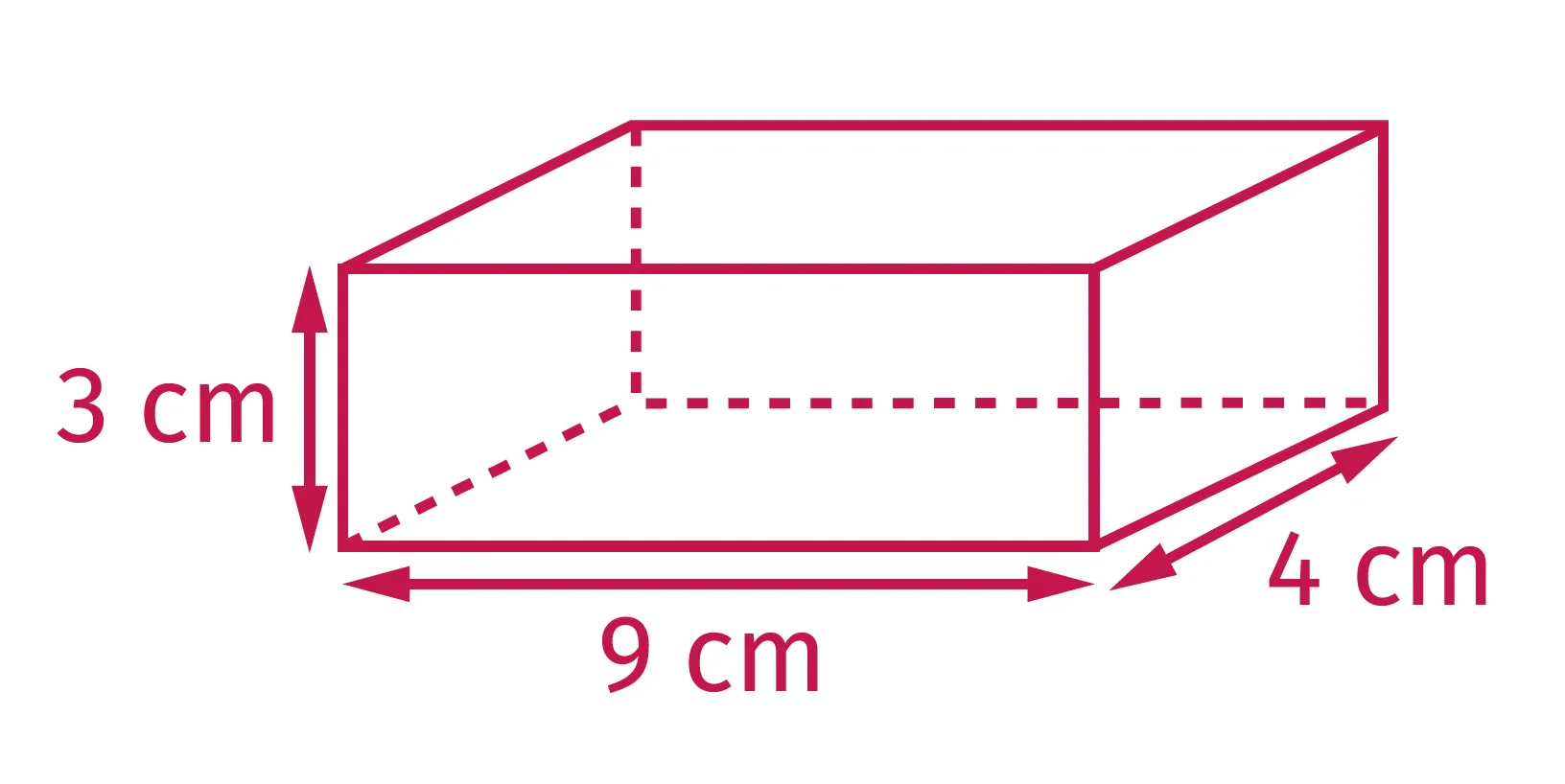
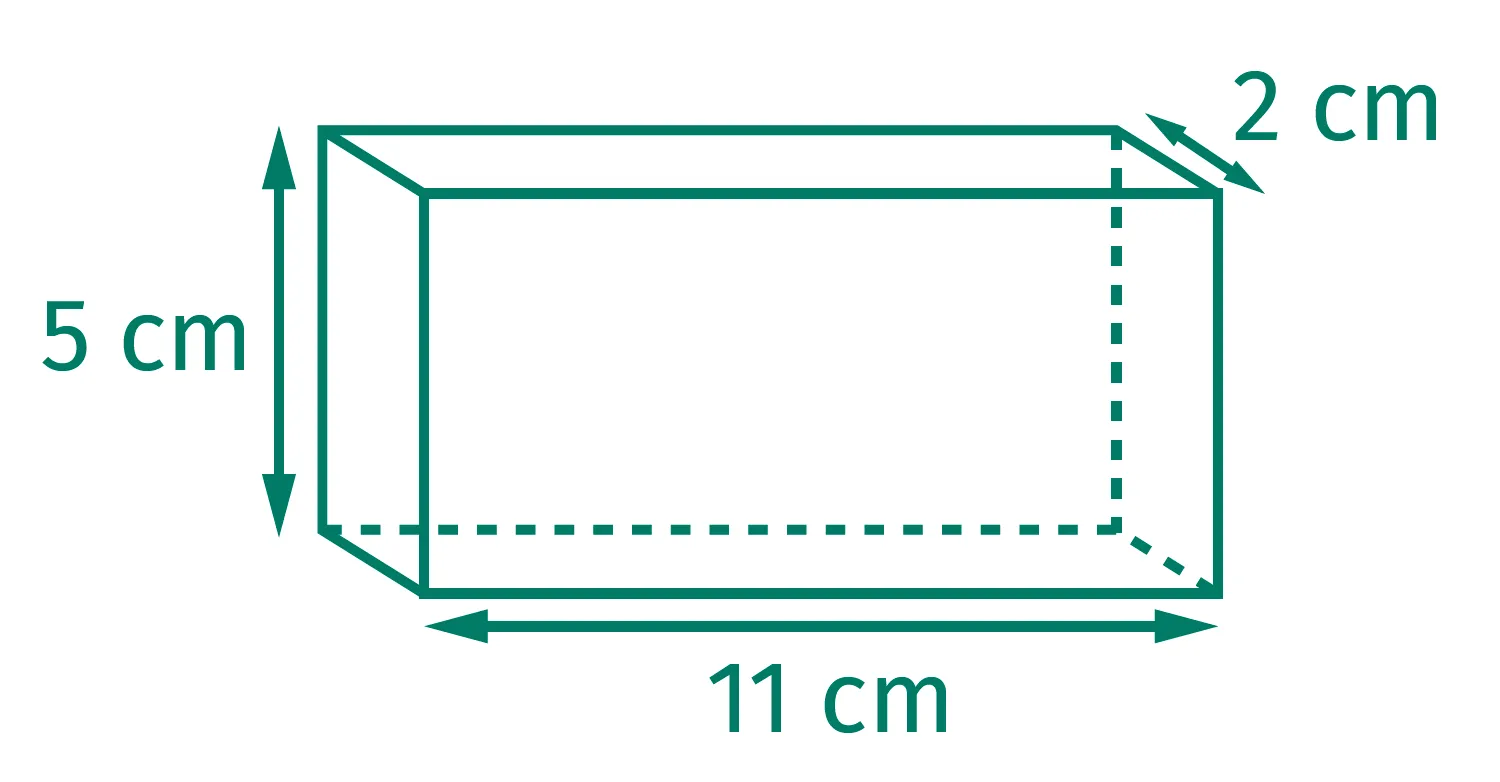
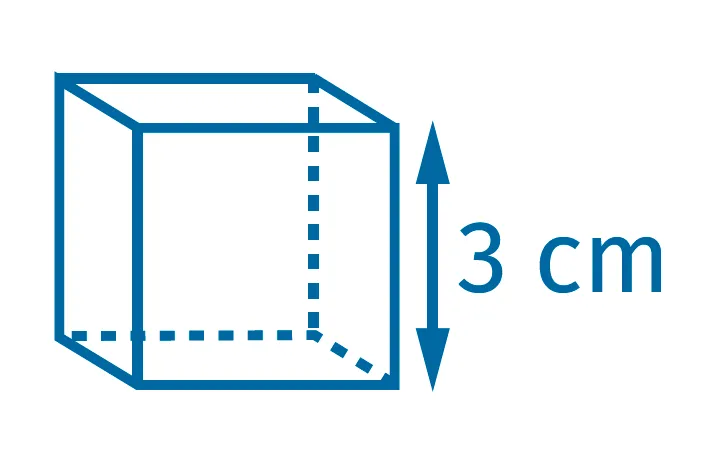
Écrire, sous chacun des solides, son volume en déterminant le nombre de cubes de 1~\mathrm{cm}^3 qu'il contient. Il y a deux pavés droits et deux cubes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
On considère le casse-tête non creux suivant constitué de cubes unités.
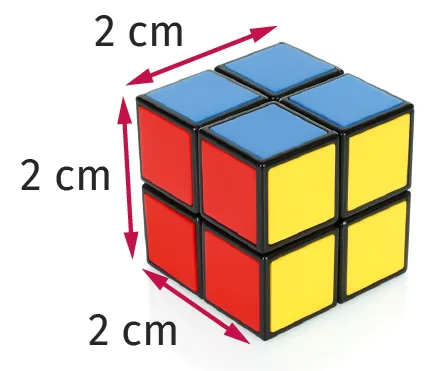
1. a. Combien de cubes unités constituent ce casse-tête ?
b. En déduire le volume d'un cube d'arête 2~\mathrm{cm}.
2. a. Combien de casse-tête seraient nécessaires pour construire un cube d'arête 4~\mathrm{cm} ?
b. En déduire le volume d'un cube d'arête 4~\mathrm{cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Déterminer le volume de ces empilements non creux de cubes unités.
1.
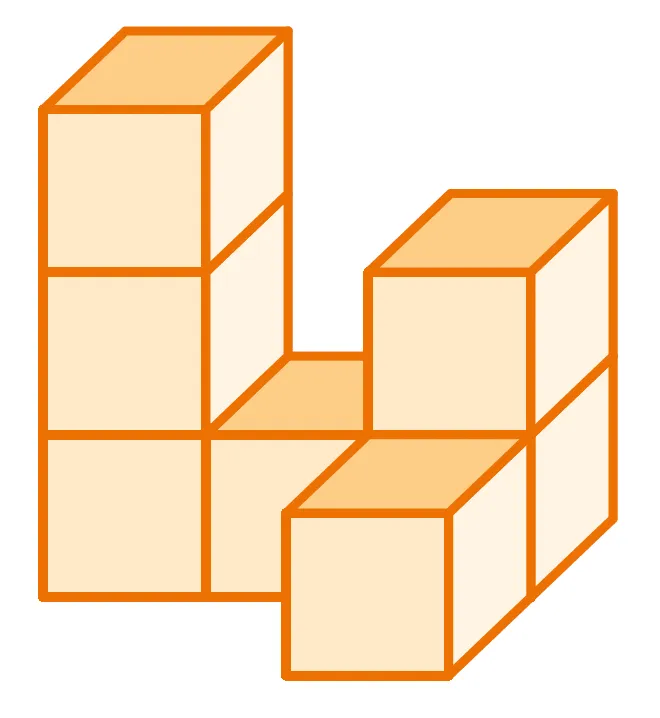
2.
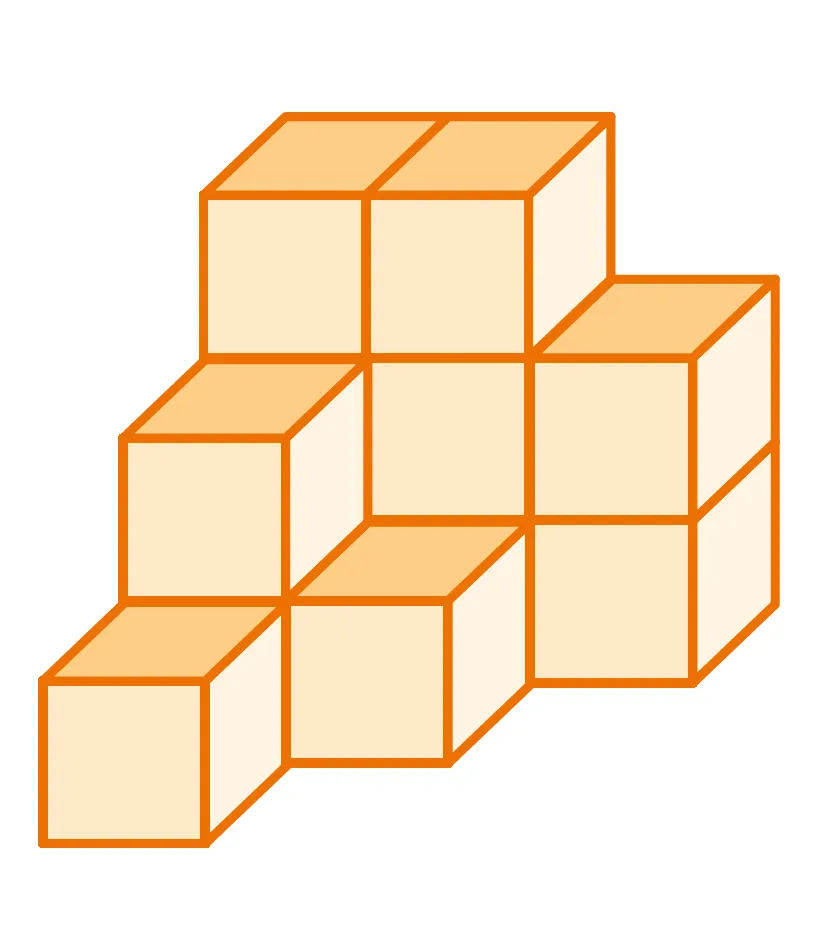
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Classer ces trois empilements non creux de cubes identiques par volume croissant.
2.
3.
1.
2.
3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Déterminer le volume total des empilements non creux de cubes de 1~\mathrm{cm}^3 ci-dessous.
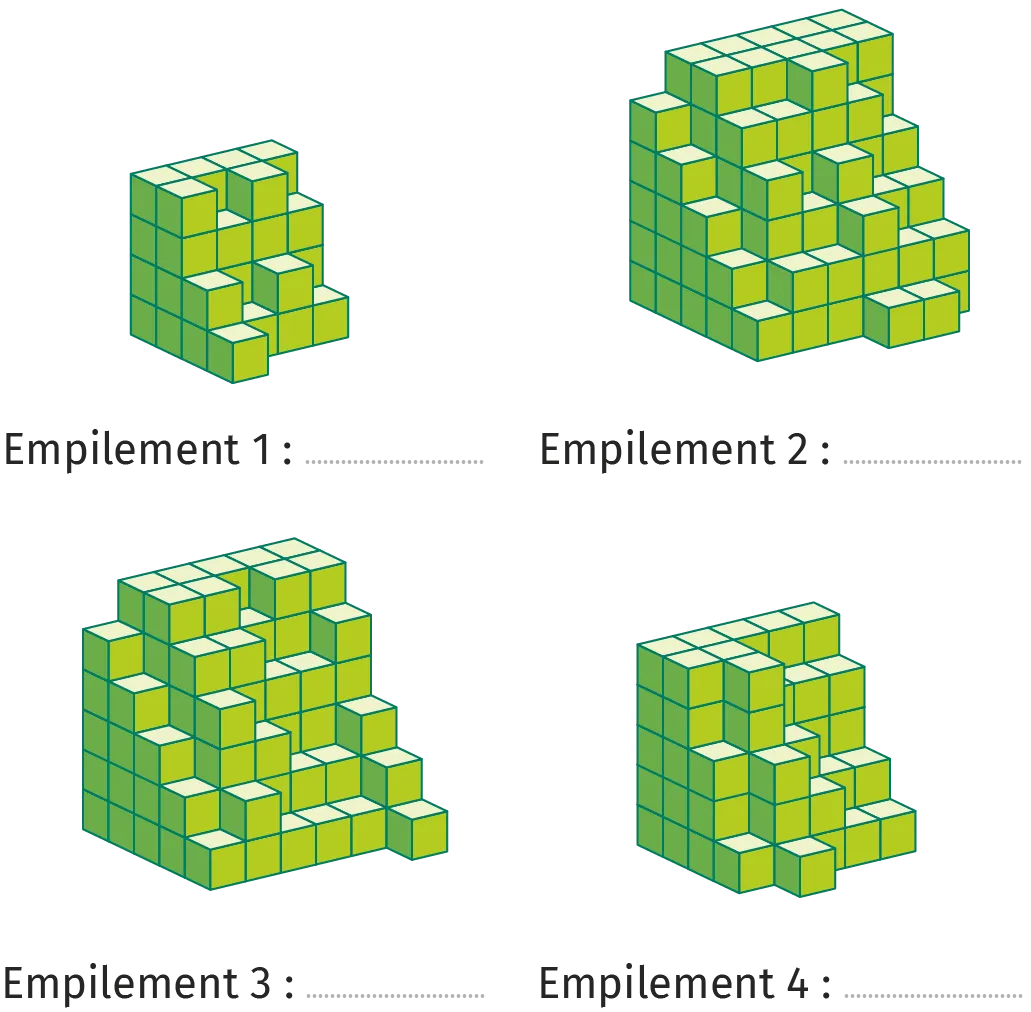
Empilement 1 :
Empilement 2 :
Empilement 2 :
Empilement 3 :
Empilement 4 :
Empilement 4 :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Énigme
Quel est le solide de plus grand volume : un cube de côté 3~\mathrm{cm} ou un pavé droit de côtés 2~\mathrm{cm}, 3~\mathrm{cm} et 4~\mathrm{cm} ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
