Thème 2 : Grandeurs et mesures
Fiche 32
Nommer et reconnaître les angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définitions
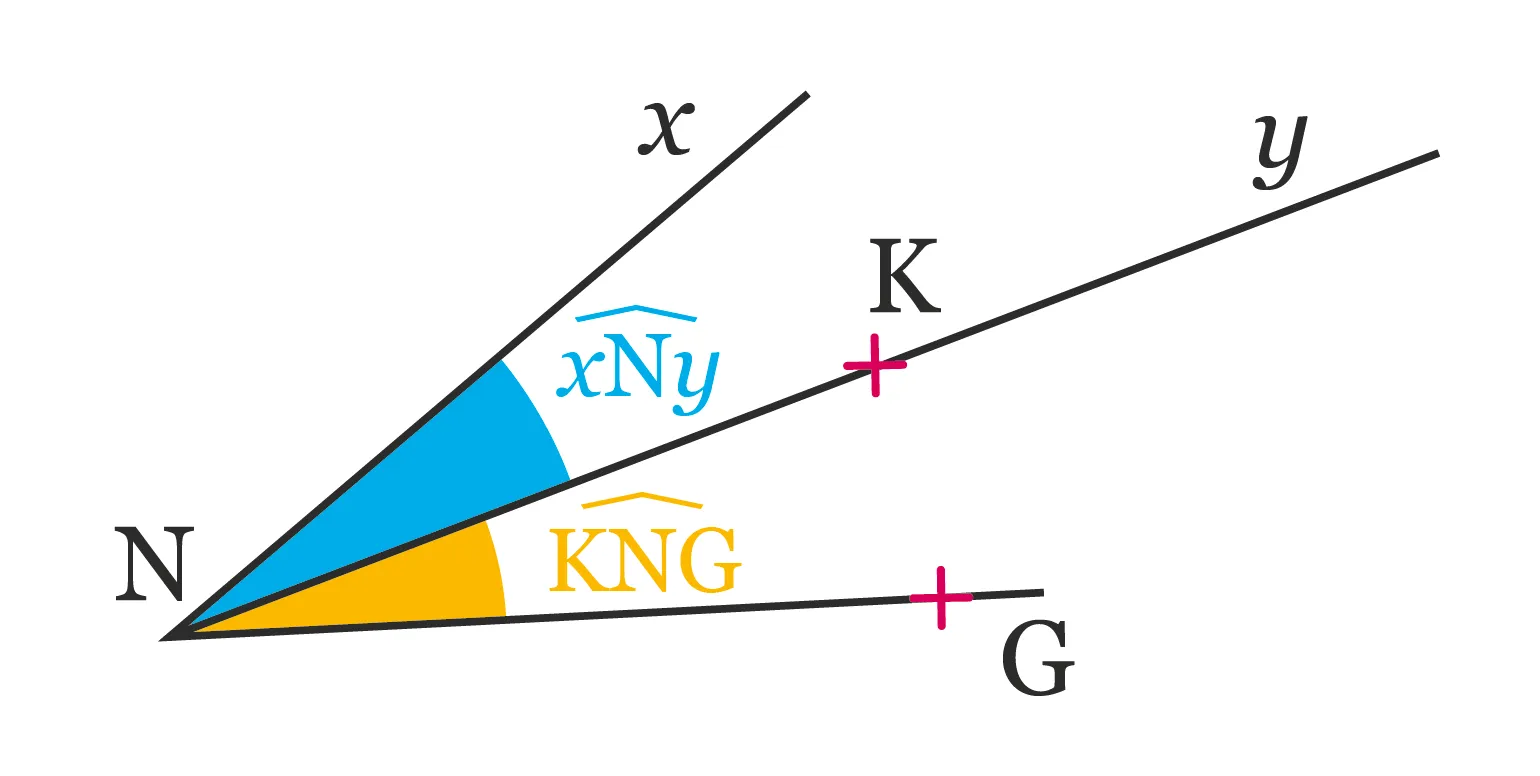
Un angle est une portion de plan délimitée par deux demi-droites de même origine, appelées côtés de l'angle. Leur origine commune est le sommet de l'angle.
Deux cas sont possibles.
- Cas 1 : Les deux demi-droites forment une droite et l'angle formé est alors appelé angle plat.
- Cas 2 : Les deux demi-droites forment deux angles correspondant à une ouverture. La plus petite des deux est appelée angle saillant et la plus grande est appelée angle rentrant.


- Remarque : Lorsque la notation est ambiguë, on la précise en utilisant des points qui appartiennent aux côtés de l'angle (ici \mathrm{K} et \mathrm{G}) ou les demi-droites qui délimitent l'angle \left[\mathrm{Nx}\right) et \left[\mathrm{Ny}\right).
Définitions
1. L'angle droit s'obtient en décomposant l'angle plat en deux angles égaux (de même ouverture).
2. Un angle aigu est un angle plus petit que l'angle droit.
3. Un angle obtus est un angle saillant plus grand que l'angle droit.
2. Un angle aigu est un angle plus petit que l'angle droit.
3. Un angle obtus est un angle saillant plus grand que l'angle droit.

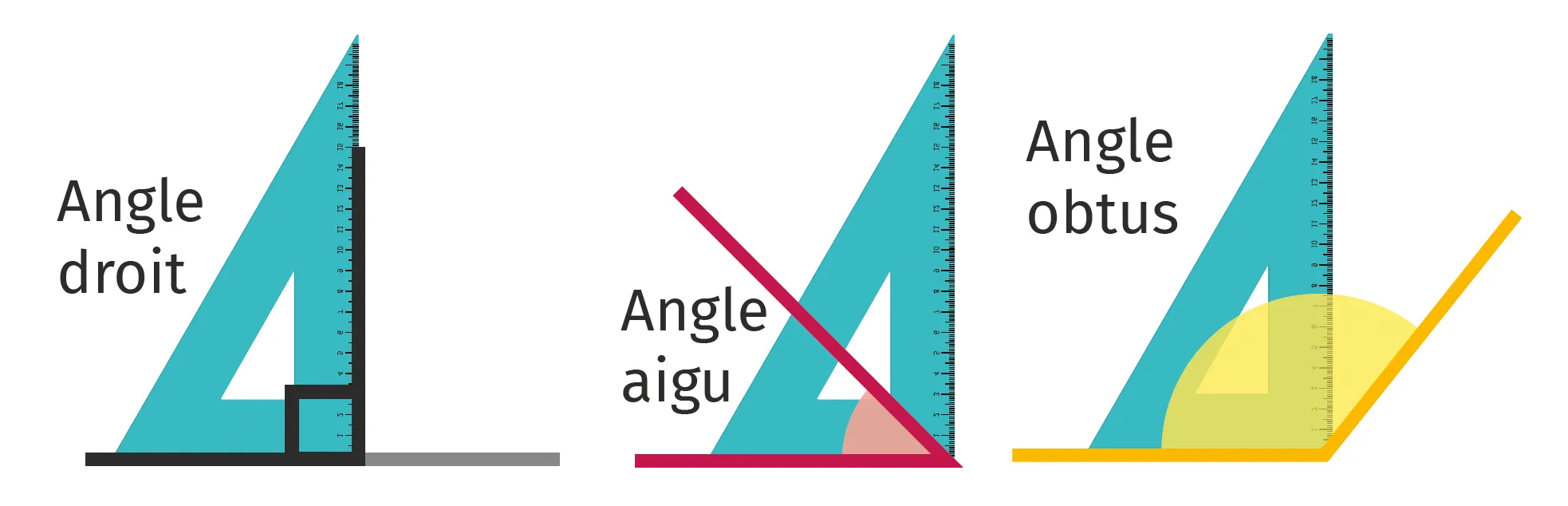
Supplément numérique
Retrouver une .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les Romains utilisaient un ancêtre de l'équerre, la groma, pour établir le tracé de routes perpendiculaires.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. \frac{3476}{100}=
2. \frac{1}{2}+\frac{1}{2}=
3. Coder les angles droits et les longueurs égales.
2. \frac{1}{2}+\frac{1}{2}=
3. Coder les angles droits et les longueurs égales.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Compléter le tableau en donnant tous les noms possibles pour chaque angle.

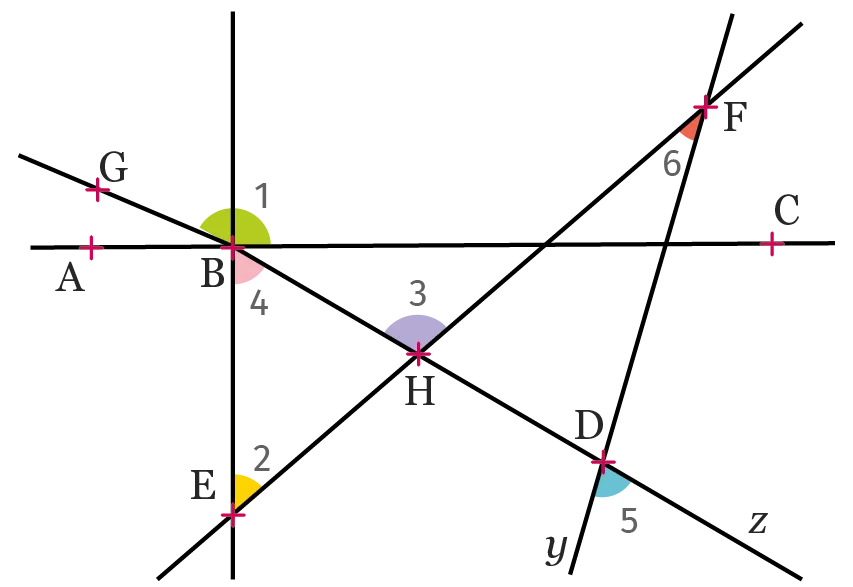


| N° de l'angle | Noms possibles de l'angle |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Compléter le tableau pour nommer les angles de la figure et donner leur nature.

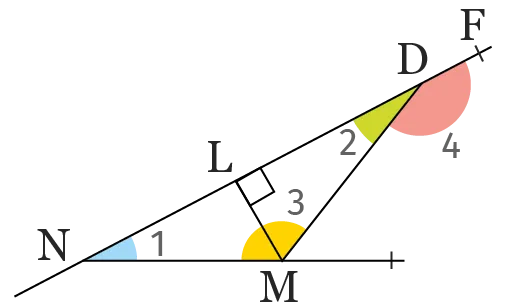


| Angle n° | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
Côtés délimitant l'angle
| [\mathrm{NL}) et [\mathrm{NM}) | |||
Nom
| \widehat{\mathrm{LNM}} ou \widehat{\mathrm{MNL}} | |||
Nature
| Aigu |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Classer les angles dans le tableau selon leur nature.
| Angle droit | Angle aigu | Angle obtus |
|---|---|---|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Copie d'élève
Copie d'élève

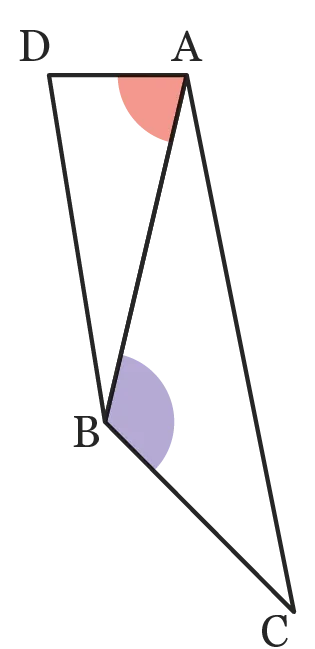
Andréa devait préciser la nature des angles de la figure.
1. Corriger sa copie.
L'angle \widehat{\mathrm{A}} est obtus et l'angle \widehat{\mathrm{B}} aussi.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Colorer d'une même couleur les angles égaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Exercice inversé
Exercice inversé
Tracer un quadrilatère \mathrm{ABCD} vérifiant les conditions suivantes : \mathrm{ABC} est aigu, \mathrm{DCB} est obtus, \mathrm{DAB} est un angle droit mais pas \mathrm{ADC}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
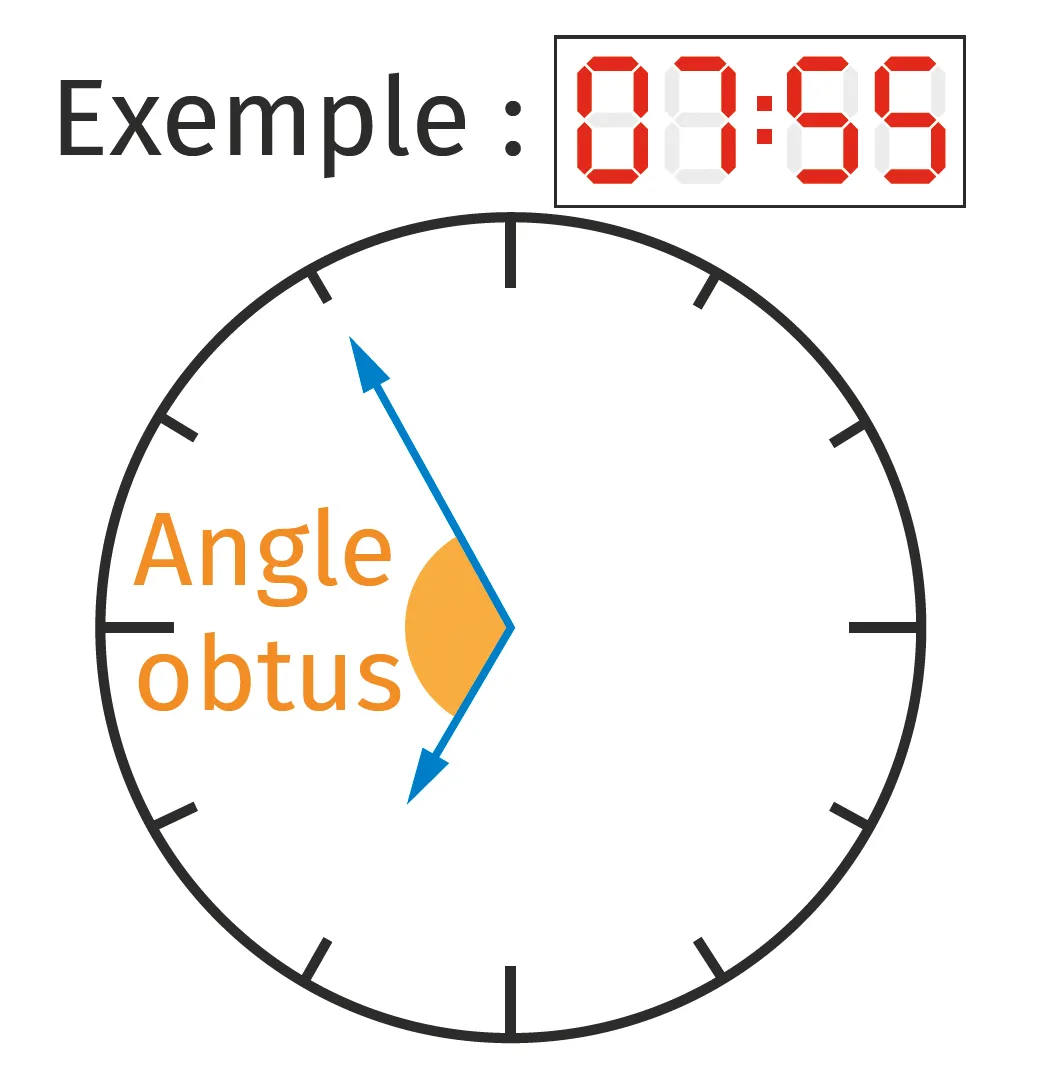
7Énigme
Entourer en bleu les réveils pour lesquels les aiguilles formeraient un angle obtus s'il s'agissait d'une horloge analogique.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


