Thème 2 : Grandeurs et mesures
Fiche 35
Utiliser les angles opposés par le sommet et les angles supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définition
Deux angles sont :
1. supplémentaires lorsqu'ils forment à eux deux un angle plat. Autrement dit, la somme des mesures des angles supplémentaires vaut 180° ;
2. adjacents lorsqu'ils ont le même sommet et un côté commun ;
3. opposés par le sommet lorsqu'ils ont le même sommet et que les côtés de l'un sont le prolongement de ceux de l'autre.
- Remarque : Deux angles supplémentaires ne sont pas toujours adjacents.
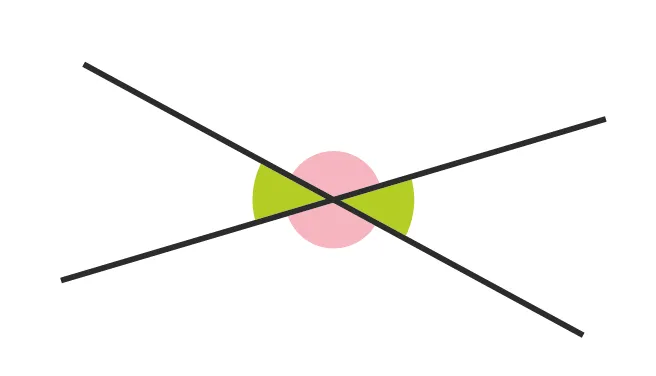
Exemple : Ici, on identifie deux paires d'angles opposés par le sommet :
une paire codée en vert, l'autre en rouge.
Une paire formée d'un angle vert et d'un angle rouge est une paire d'angles supplémentaires.
Propriété
Si deux angles sont opposés par le sommet, alors ils ont la même mesure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut construire des sous-unités du degré,
par exemple la minute d'arc, notée ', pour
laquelle on a l'égalité : 1' = \frac{1°}{60}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. \frac{3~207}{1~000}=
2. \frac{1}{4}+\frac{1}{4}=
3. Les multiples de 7 inférieurs à 30 :
2. \frac{1}{4}+\frac{1}{4}=
3. Les multiples de 7 inférieurs à 30 :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Copie d'élève
Copie d'élève
Aimée doit construire l'angle opposé par le sommet à l'angle \widehat{\mathrm{ABC}} sur la figure ci-dessous. Voici ce qu'elle propose.
1. Construire un contre-exemple sur la figure ci-dessous pour lui montrer que sa description est incomplète.
2. Comment construire l'angle demandé ?
Il faut construire deux demi-droites [\mathrm{BD}) et [\mathrm{BE}) qui forment un angle de 30°.
1. Construire un contre-exemple sur la figure ci-dessous pour lui montrer que sa description est incomplète.
2. Comment construire l'angle demandé ?
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Sur la figure ci-dessous, les droites \mathrm{(AD)} et \mathrm{(CE)} sont sécantes au point \mathrm{B}.
1. Indiquer les paires d'angles supplémentaires que l'on peut former.
2. a. Mesurer chacun des quatre angles de sommet B et calculer les sommes des mesures de chaque paire d'angles adjacents.
b. Que constate-t-on ?
1. Indiquer les paires d'angles supplémentaires que l'on peut former.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
1. Sur la figure ci-dessous, placer un point \mathrm{C} n'appartenant pas à la droite \mathrm{(AB)} et tracer la droite \mathrm{(BC)}.
2. Mesurer l'angle \widehat{\mathrm{ABC}} et celui qui lui est opposé par le sommet. Que constate-t-on ?
3. Tracer la droite \mathrm{(AC)}. Mesurer l'angle \widehat{\mathrm{BAC}} et celui qui lui est opposé par le sommet. Que constate-t-on ?
2. Mesurer l'angle \widehat{\mathrm{ABC}} et celui qui lui est opposé par le sommet. Que constate-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
On donne la figure ci-dessous.

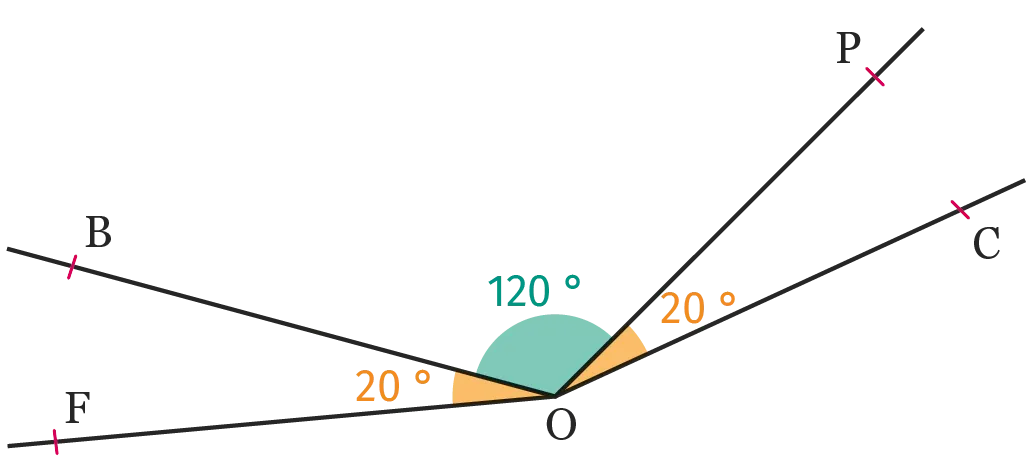
3. Les angles \widehat{\mathrm{BOP}} et \widehat{\mathrm{POC}} sont-ils adjacents ?


1. Les angles \widehat{\mathrm{BOF}} et \widehat{\mathrm{POC}} sont-ils opposés par le sommet ?
2. Les angles \widehat{\mathrm{BOF}} et \widehat{\mathrm{BOP}} sont-ils supplémentaires ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
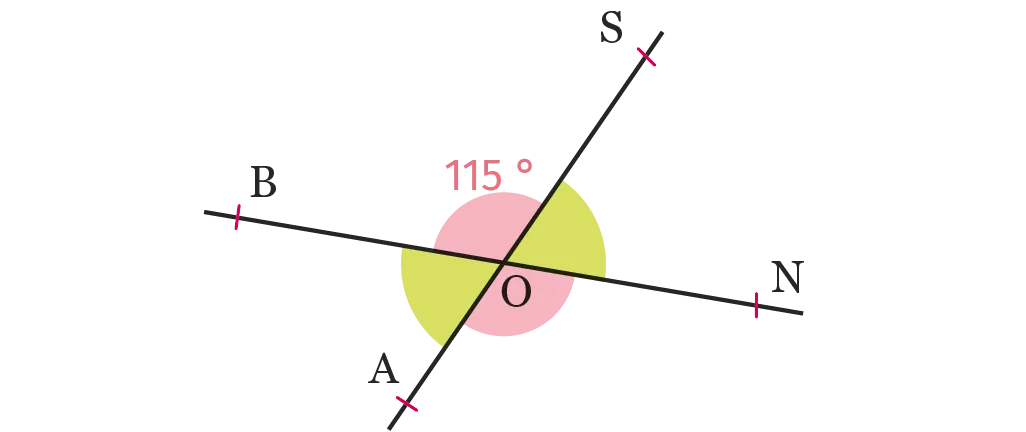
Sur la figure ci-dessous, les droites \mathrm{(BN)} et \mathrm{(AS)} sont sécantes au point \text{O}. Déterminer les mesures des angles \widehat{\mathrm{BOA}}, \widehat{\mathrm{NOA}} et \widehat{\mathrm{SON}}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Énigme
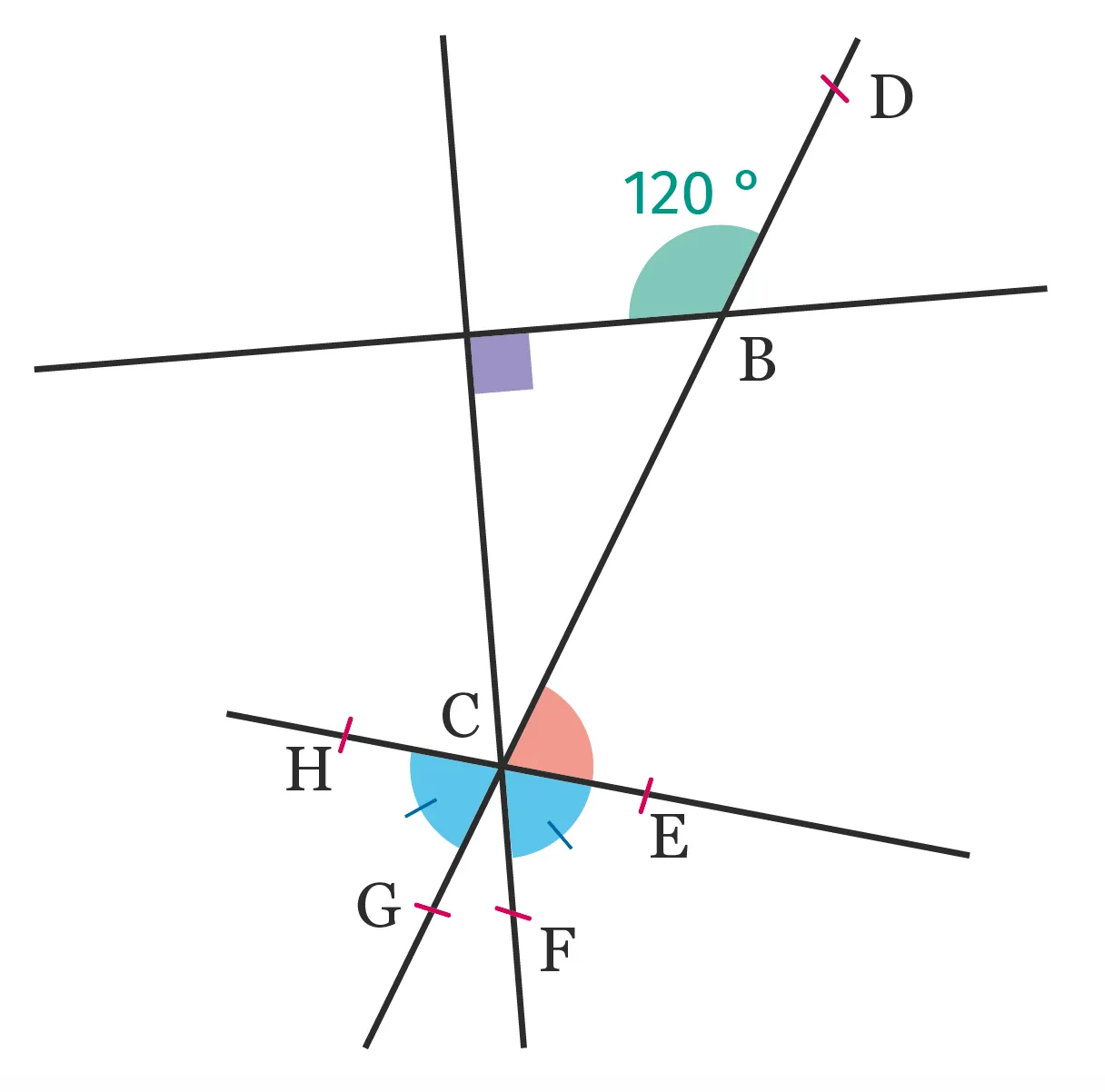
Déterminer la mesure de l'angle \widehat{\mathrm{BCE}}.



Coup de pouce
La somme des mesures des trois angles d'un triangle vaut 180°.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


