Thème 3 : Espace et géométrie
Fiche 37
Déterminer et utiliser la distance entre deux points
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définition
La distance entre deux points est la longueur du plus court chemin entre eux.
Propriété
Le plus court chemin entre deux points \mathrm{A} et \mathrm{B} est le segment [\mathrm{AB}].

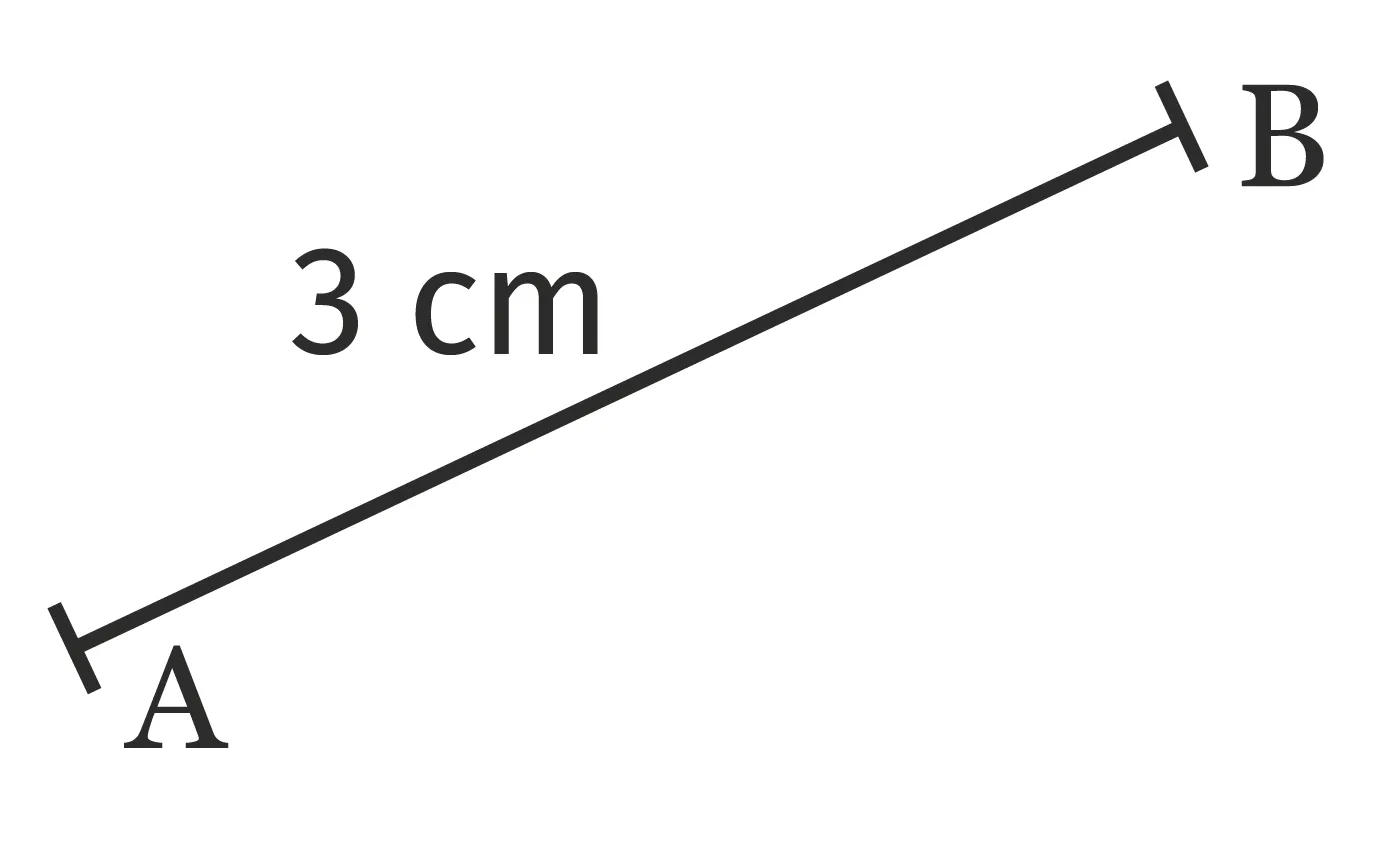
On note \mathrm{AB} = 3~\mathrm{cm}.
La distance entre \mathrm{A} et \mathrm{B} est de 3~\mathrm{cm}.
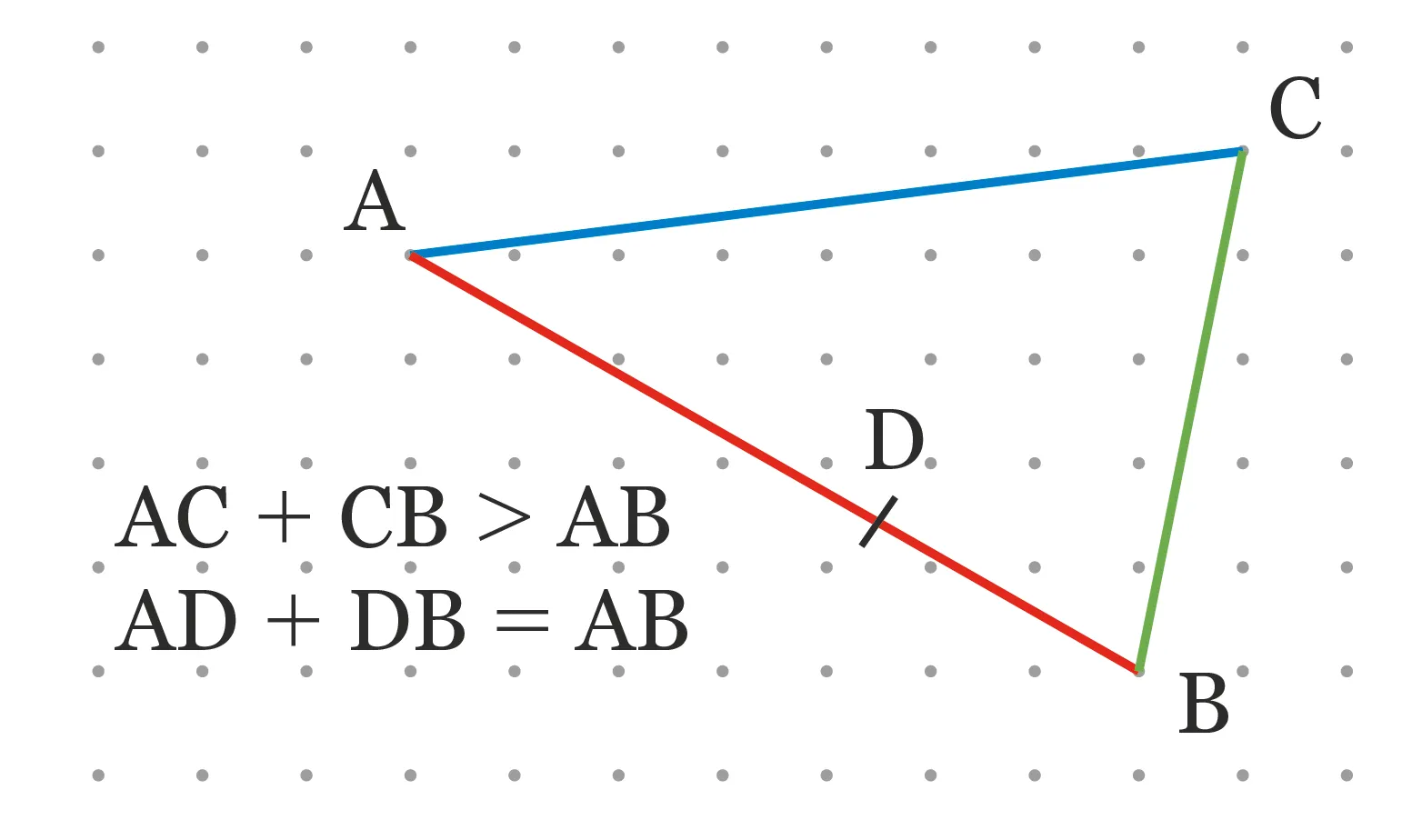
Conséquences :
- Si \mathrm{C} n'appartient pas à [\mathrm{AB}], alors \mathrm{AC} + \mathrm{CB} > \mathrm{AB}.
- Si \mathrm{D} appartient à [\mathrm{AB}], alors \mathrm{AD} + \mathrm{DB} = \mathrm{AB}.

Supplément numérique
Retrouver une .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Lorsque \mathrm{C} n'appartient pas à \mathrm{[AB]}, l'inégalité
\mathrm{AC+CB>AB} est appelée inégalité triangulaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 2 + \frac{4}{10} + \frac{3}{1000} =
2. Un quart d'heure : min
3. 1 - \frac{1}{4} =
2. Un quart d'heure :
3. 1 - \frac{1}{4} =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
1. À partir des figures ci-dessous, compléter avec les symboles « appartient » (∈) ou « n'appartient pas » (∉).

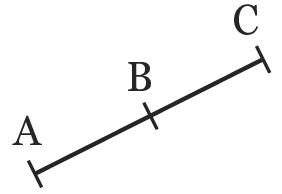
a. \text{C} [AB]

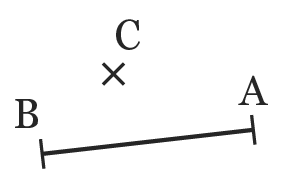
b. \text{C} [AB]


c. \text{C} [AB]
2. Mesurer sur les figures et compléter le tableau suivant.
3. Dans quel cas peut-on affirmer que \mathrm{AC + CB = AB} ?


a. \text{C} [AB]


b. \text{C} [AB]


c. \text{C} [AB]
2. Mesurer sur les figures et compléter le tableau suivant.
| n° | \mathrm{AC + CB} | > ou = | \mathrm{AB} |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 |
3. Dans quel cas peut-on affirmer que \mathrm{AC + CB = AB} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Dans chaque cas, compléter avec un symbole d'égalité ou d'inégalité.

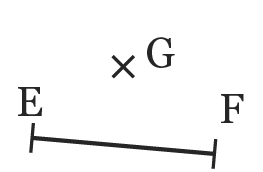
1. \mathrm{EF} \mathrm{EG + GF}

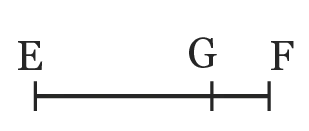
2. \mathrm{EF} \mathrm{EG + GF}


3. \mathrm{EF} \mathrm{EG + GF}


4. \mathrm{EF} \mathrm{EG + GF}

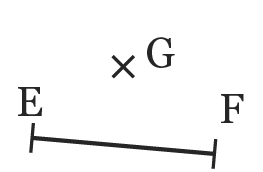
1. \mathrm{EF} \mathrm{EG + GF}

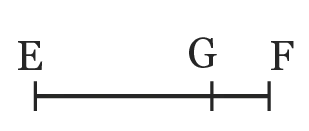
2. \mathrm{EF} \mathrm{EG + GF}


3. \mathrm{EF} \mathrm{EG + GF}


4. \mathrm{EF} \mathrm{EG + GF}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Copie d'élève
Copie d'élève
Corriger la copie de Kaïs.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Compléter les phrases suivantes à partir de la figure ci-dessous.

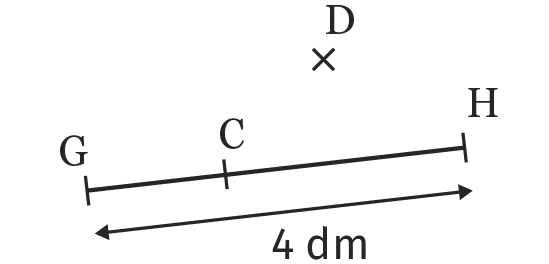
Le segment est le plus court chemin entre \mathrm{G} et \mathrm{H}. Sa longueur est : = 4~\mathrm{dm}.
De plus, \mathrm{C} [\mathrm{GH}]. Donc on a \mathrm{GC + CH} \mathrm{GH}.
Enfin, \mathrm{D} [\mathrm{GH}]. Donc on a \mathrm{GD + DH} \mathrm{GH}.


Le segment
De plus, \mathrm{C}
Enfin, \mathrm{D}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
En utilisant uniquement le compas, ranger les longueurs des segments dans l'ordre croissant.
\lt \lt \lt \lt
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Quels sont les deux points de la figure formant le segment le plus court ? Le plus long ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Deux équipes s'affrontent au jeu du béret.
Depuis leur ligne de départ, les joueurs doivent
courir jusqu'au béret et le ramener dans leur camp.
1. Placer le béret \mathrm{( B )} de manière à ce qu'il soit situé exactement entre Flora \mathrm{( F )} et Samir \mathrm{( S )}.
2. On conserve le placement du béret. Placer Laura \mathrm{( L )} dans l'équipe 1 pour qu'elle soit à la même distance du béret que Mohamed \mathrm{( M )}.
1. Placer le béret \mathrm{( B )} de manière à ce qu'il soit situé exactement entre Flora \mathrm{( F )} et Samir \mathrm{( S )}.
2. On conserve le placement du béret. Placer Laura \mathrm{( L )} dans l'équipe 1 pour qu'elle soit à la même distance du béret que Mohamed \mathrm{( M )}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Énigme
Dans ce jeu, le but est d'amener son pion dans le camp adverse. À son tour, on peut soit le déplacer d'une case à la verticale ou à l'horizontale, soit poser une barrière de la longueur d'un carreau pour bloquer le passage.
C'est au tour du pion rouge de jouer et le joueur souhaite poser une barrière.
1. Placer une barrière pour allonger au maximum le parcours du pion bleu.
2. Tracer ensuite le plus court chemin entre le pion bleu et le camp rouge.
3. Si aucune autre barrière n'est posée par les joueurs, quel pion atteindra le camp adverse en premier ?
C'est au tour du pion rouge de jouer et le joueur souhaite poser une barrière.
1. Placer une barrière pour allonger au maximum le parcours du pion bleu.
2. Tracer ensuite le plus court chemin entre le pion bleu et le camp rouge.
3. Si aucune autre barrière n'est posée par les joueurs, quel pion atteindra le camp adverse en premier ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


