Thème 3 : Espace et géométrie
Fiche 47
Construire la bissectrice d'un angle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définition
La droite bissectrice d'un angle est la droite qui partage cet angle en deux angles adjacents égaux.
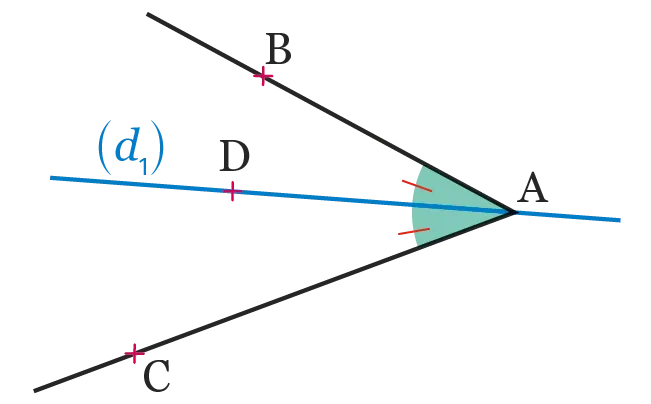
Exemple : Sur la figure ci-contre, la droite (d_1) est la bissectrice de l'angle \widehat{\mathrm{BAC}} : elle partage cet angle en deux angles \widehat{\mathrm{BAD}} et \widehat{\mathrm{DAC}} qui sont adjacents et qui ont la même mesure.

Propriété
La bissectrice d'un angle est l'axe de symétrie de cet angle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une trisectrice d'un angle est l'une des deux
droites qui partagent un angle en trois angles
de même mesure. À l'inverse de la bissectrice,
il est impossible, dans le cas général, de tracer
une trisectrice en utilisant uniquement le
compas et la règle non graduée.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. \frac{5}{2}=
2. \frac{1~002}{100}=


2. \frac{1~002}{100}=
3. À quelle fraction de la figure correspond la partie violette ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
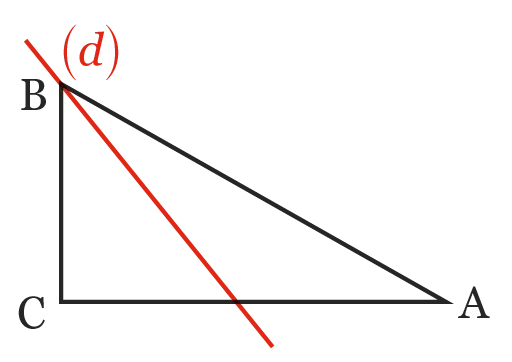
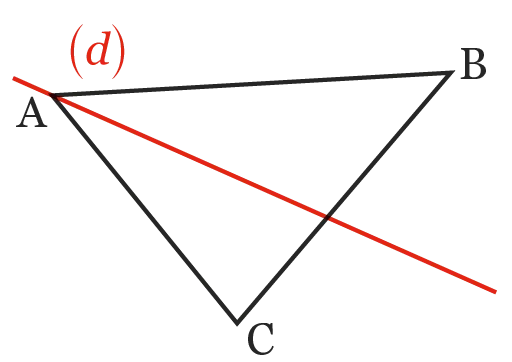
Dans chaque cas, déterminer si la droite (d) est la bissectrice de l'angle indiqué.

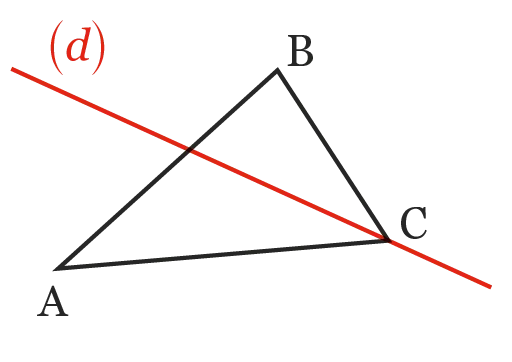


1. (d) est la bissectrice de l'angle \widehat{\mathrm{ACB}}.


2. (d) est la bissectrice de l'angle \widehat{\mathrm{ABC}}.


3. (d) est la bissectrice de l'angle \widehat{\mathrm{BAC}} .


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
À l'aide du rapporteur, construire, dans chaque cas, les bissectrices des trois angles du triangle \mathrm{ABC}.
1.
2.
1.
2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Sur la figure ci-dessous, placer des points \mathrm{E} et \mathrm{F} tels que la droite \mathrm{(AB)} soit la bissectrice de l'angle \widehat{\mathrm{CAE}} et de l'angle \widehat{\mathrm{DBF}} .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
On a tracé ci-dessous un triangle \mathrm{DEF} rectangle en \mathrm{D} tel que \widehat{\mathrm{DFE}} = 30°.
1. Calculer la mesure de l'angle \widehat{\mathrm{FED}} .
2. Tracer la bissectrice (d₁) de l'angle \widehat{\mathrm{FDE}} .
3. Tracer la bissectrice (d₂) de l'angle \widehat{\mathrm{DEF}} .
On nomme \mathrm{M} le point d'intersection des droites (d₁) et (d₂).
4. On souhaite déterminer la mesure de l'angle \widehat{\mathrm{DME}}.
a. Quelle est la mesure de l'angle \widehat{\mathrm{MDE}} ?
b. Quelle est la mesure de l'angle \widehat{\mathrm{MED}} ?
c. En déduire la mesure de l'angle \widehat{\mathrm{DME}}.
1. Calculer la mesure de l'angle \widehat{\mathrm{FED}} .
3. Tracer la bissectrice (d₂) de l'angle \widehat{\mathrm{DEF}} .
On nomme \mathrm{M} le point d'intersection des droites (d₁) et (d₂).
4. On souhaite déterminer la mesure de l'angle \widehat{\mathrm{DME}}.
a. Quelle est la mesure de l'angle \widehat{\mathrm{MDE}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
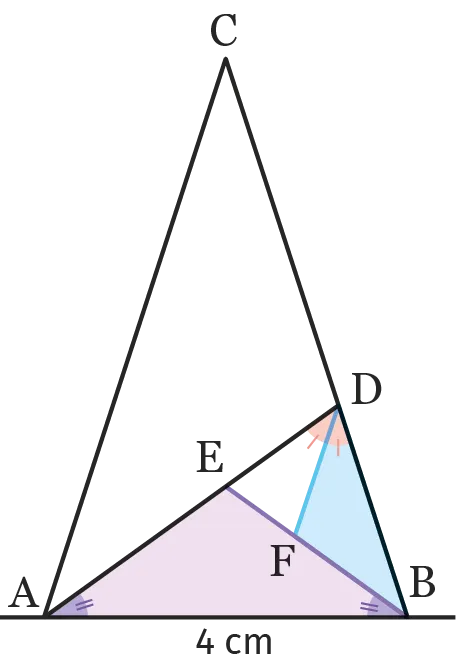
Le triangle \mathrm{ABC} ci-contre est un triangle d'or : il est isocèle en \mathrm{C} et les angles à sa base mesurent \mathrm{72°}.
Le triangle \mathrm{ABE}, est un triangle d'argent : il est isocèle \mathrm{E} et les angles à sa base mesurent \mathrm{36°}.
Écrire un protocole de construction de la figure.
Le triangle \mathrm{ABE}, est un triangle d'argent : il est isocèle \mathrm{E} et les angles à sa base mesurent \mathrm{36°}.
Écrire un protocole de construction de la figure.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Énigme

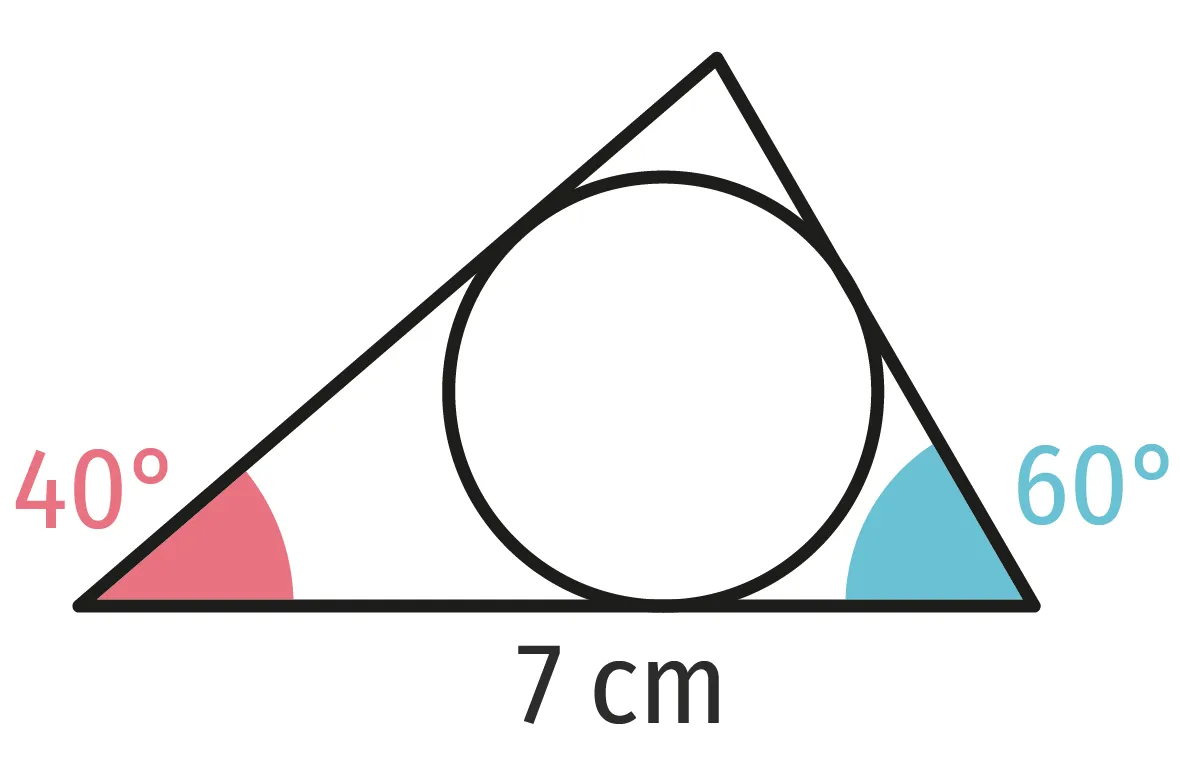
Construire en vraie grandeur la figure ci-contre.
Cliquez pour accéder à GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

