Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d’équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Chapitre 2
Bilan
Addition et soustraction de nombres rationnels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21QCM[Mod.1 - Cal.1 - Cal.4]
Cocher la (ou les) bonne(s) réponse(s).
1. La décomposition en produit de facteurs premiers de 90 est :
2. La fraction \frac{3465}{6030} :
3. On a \frac{1}{3}+\frac{3}{4}=
4. Loïc mange les \frac{2}{8} d'un paquet de bonbons. Il en reste alors les :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22[Rais.4 - Cal.1 - Cal.5]
On considère la fraction \frac{5850}{2340}.
1. Sans calcul, expliquer pourquoi on peut simplifier cette fraction.
2. Décomposer en produit de facteurs premiers les nombres 5~580 et 2~340.
3. En déduire la forme la plus simplifiée possible de \frac{5~850}{2~340}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23[Mod.1 - Rais.4 - Cal.4]
D'après Brevet, Nouvelle-Calédonie, 2018
1. Décomposer les nombres 162 et 108 en produits de facteurs premiers.
2. Déterminer deux diviseurs communs aux nombres 162 et 108 plus grands que 10.
3. Un snack vend des barquettes composées de nems et de samoussas. Le cuisinier a préparé 162 nems et 108 samoussas. Dans chaque barquette :
- le nombre de nems doit être le même ;
- le nombre de samoussas doit être le même.
a. Le cuisinier peut-il réaliser 36 barquettes ?
b. Quel nombre maximal de barquettes pourra‑t‑il réaliser ?
c. Dans ce cas, combien y aura‑t‑il de nems et de samoussas dans chaque barquette ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24[Mod.1 - Cal.1 - Cal.4]
Lydia participe à une course composée de trois épreuves : \frac{1}{6} de la distance à parcourir se fait à pied, \frac{9}{20} se fait en vélo et le reste en nageant.
Calculer la proportion de la distance à parcourir à la nage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25[Cal.1 - Cal.4]
Calculer, puis donner le résultat sous la forme d'une fraction la plus simple possible.
1. \text{A}=2-\frac{4}{9}+\frac{5}{3}
2. \text{B}=\frac{1}{3}+\frac{5}{6}-\frac{4}{7}
3. \text{C}=4-\left(\frac{2}{3}-\frac{3}{4}\right)
4. \text{D}=-\frac{7}{8}+\frac{3}{-2}+\frac{-9}{16}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26[Cal.1 - Cal.4]
Le zoom est accessible dans la version Premium.
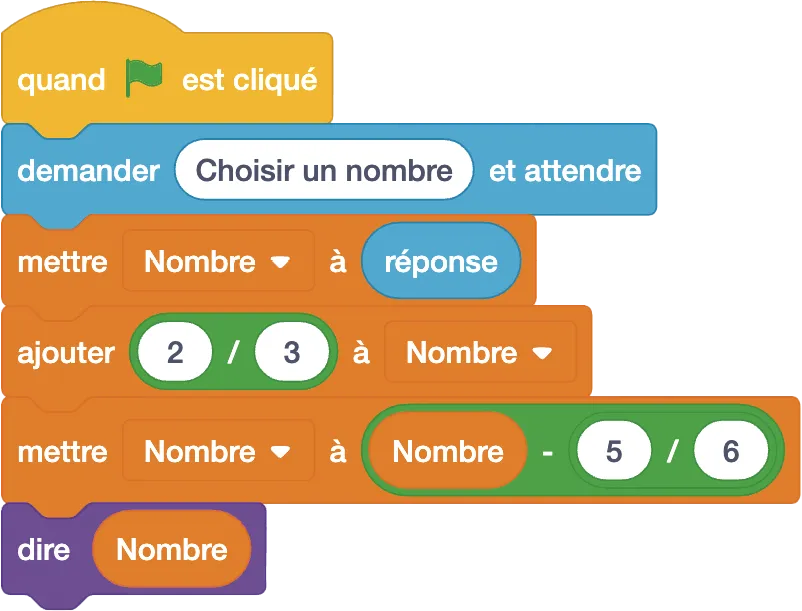
1. Vérifier que si le nombre choisi initialement est \frac{2}{9}, alors on obtient \frac{1}{18} comme résultat.
2. Qu'obtient-on comme résultat si on choisit \frac{3}{7} en nombre de départ ?
2. Qu'obtient-on comme résultat si on choisit \frac{3}{7} en nombre de départ ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27[Cal.2 - Rais.2 - Ch.1]
Dans le rayon d'un supermarché, un client analyse les informations nutritionnelles de deux pâtes à tartiner.
| Pâte à tartiner A | Pâte à tartiner B |
|---|---|
|
|
Le client souhaite acheter la pâte à tartiner contenant la proportion de noisettes la plus importante. Laquelle va-t-il choisir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28[Mod.1 - Cal.1 - Cal.4 - Ch.2]
Peut‑on construire un triangle dont les côtés
mesurent \frac{13}{8} \mathrm{~cm}, \frac{5}{2} \mathrm{~cm} et \frac{9}{4} \mathrm{~cm} ?Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Genially
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah