Chapitre 3
Exercices d'entraînement
Multiplication et division de nombres rationnels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer une suite d'opérations de nombres rationnels
Propriété :
Pour calculer une expression contenant plusieurs opérations différentes, il faut respecter les priorités opératoires, c'est-à-dire effectuer dans l'ordre :
1. les calculs entre parenthèses ;
2. les multiplications et divisions de gauche à droite ;
3. les additions et soustractions de gauche à droite.
Exemples :
1. \frac{1}{5}+\frac{2}{5} \div \frac{5}{7}=\frac{1}{5}+\frac{2}{5} \times \frac{7}{5}=\frac{1}{5}+\frac{14}{25}=\frac{5}{25}+\frac{14}{25}=\frac{19}{25}
2. \left(\frac{3}{5}+\frac{1}{4}\right) \times \frac{5}{2}=\left(\frac{12}{20}+\frac{5}{20}\right) \times \frac{5}{2}=\frac{17}{20} \times \frac{5}{2}=\frac{17 \times \color{#C62A58}\cancel{\color{#000000}5}}{{\color{#C62A58}\cancel{\color{#000000}5}} \times 4 \times 2}=\frac{17}{8}
Retrouvez et .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21[Mod.2]
Recopier l'opération prioritaire de chaque calcul.
1. \frac{2}{3}-\left(\frac{5}{6}+\frac{1}{6}\right)
2. \frac{4}{9} \times 25 \div \frac{1}{5}
3. \frac{8}{7}-\frac{1}{7} \times \frac{5}{11}
4. \frac{4}{3} \div\left(2+\frac{1}{4}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Inversé[Rais.6 - Com.1]
Écrire un programme de calcul qui traduit
le calcul \frac{7}{6} \div\left(x-\frac{4}{9}\right), où x désigne le nombre de départ.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22[Cal.1 - Cal.4]
Calculer en simplifiant au maximum.
1. \text{A}=\frac{3}{2}+\frac{5}{4}-\frac{5}{8}
2. \text{B}=\frac{3}{4} \times \frac{5}{6} \div \frac{1}{8}
3. \text{C}=\frac{4}{9}-\frac{7}{9} \times \frac{3}{4}
4. \text{D}=\left(\frac{7}{3}-\frac{2}{7}\right) \times \frac{-7}{2}
5. \text{E}=-\frac{5}{6}+\frac{11}{6} \div \frac{22}{18}
6. \text{F}=8 \div\left(\frac{3}{4}+\frac{7}{6}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24[Mod.1 - Cal.1 - Cal.4]
Les \frac{8}{9} des 150 places d'un spectacle ont été vendues, \frac{1}{4} d'entre elles à des adultes.
1. Quel calcul doit-on effectuer pour déterminer le nombre d'enfants assistant à ce spectacle ?
2. Déterminer ce nombre d'enfants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25[Cal.1 - Cal.4]

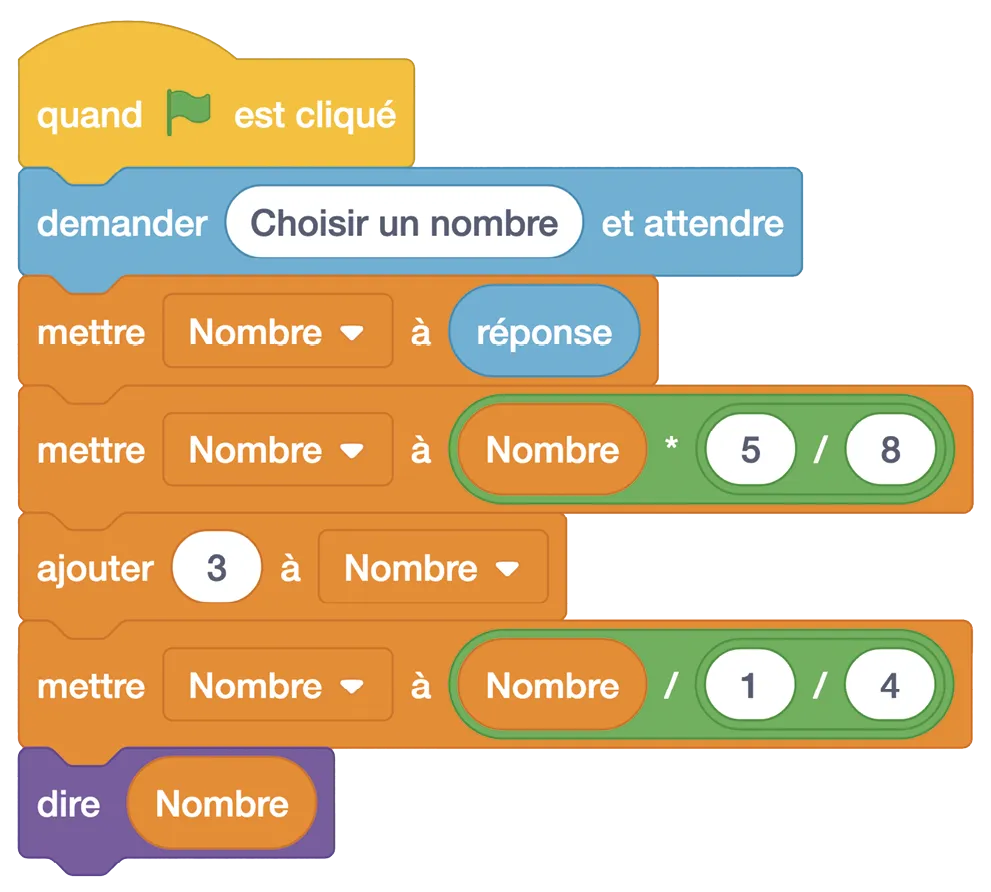
1. Vérifier que si l'on choisit \frac{16}{3} au départ, on obtient \frac{76}{3} en sortie de programme.
2. Qu'obtient-on en sortie de programme si on choisit \frac{-8}{9} au départ ?
3. Quel nombre doit-on choisir au départ pour obtenir 0 en sortie de programme ? Justifier.
2. Qu'obtient-on en sortie de programme si on choisit \frac{-8}{9} au départ ?
3. Quel nombre doit-on choisir au départ pour obtenir 0 en sortie de programme ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26[Cal.1 - Cal.4]
Calculer en simplifiant au maximum.
1. \text{G}=\frac{\frac{1}{4}+\frac{2}{3}}{2}
2. \text{H}=\frac{\frac{4}{5}}{\frac{9}{10}}-\frac{2}{3}
3. \text{I}=\frac{\frac{-7}{6}}{4+\frac{5}{6}}
4. \text{J}=\frac{\frac{5}{2}-\frac{9}{4}}{1-\frac{3}{8}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 12+\frac{120}{60}=
2. \frac{25}{2}-5=
2. \frac{25}{2}-5=
3. 45 \times \frac{20}{40}=
4. \left(\frac{1}{6}+\frac{11}{6}\right) \times 621=
4. \left(\frac{1}{6}+\frac{11}{6}\right) \times 621=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le coin des experts
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
On pose x=\frac{5}{4}, y=\frac{-1}{12} et z=\frac{5}{6}.
Calculer le produit de z par l'inverse de la somme de x et de y.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

