Chapitre 3
Bilan
Multiplication et division de nombres rationnels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28QCM[Mod.1 - Cal.1 - Cal.4]
Cocher la (ou les) bonne(s) réponse(s).
1. On a \frac{4}{3}-\frac{1}{3} \div \frac{3}{7}=
2. On a -\frac{7}{9} \times \frac{3}{5}=
3. Les \frac{4}{7} de 49~€ font :
4. Les \frac{3}{8} d'un nombre font 24. Ce nombre vaut alors :
5. L'inverse de l'opposé de \frac{1}{3} est égal à :
6. Léo le chat mange le quart de ses croquettes le matin. Il en mange le tiers du reste l'après-midi. Il reste alors :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29[Mod.1 - Cal.1 - Cal.4]
Dans un collège, 66 % des 150 élèves de troisième
ont obtenu le diplôme national du brevet avec une mention. Dans le collège voisin, 70 % des 120 élèves de troisième ont obtenu une mention.Dans quel collège compte‑t‑on le plus de lauréats avec mention ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30[Mod.1 - Cal.1 - Cal.4]
Mathilde a dépensé les \frac{8}{15} de ses 120~€ pour acheter un jeu vidéo. Combien lui reste-t-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31[Mod.1 - Cal.1 - Cal.4]
Il reste les \frac{8}{9} d'une galette des rois. Quatre amis
veulent se partager ce reste équitablement. Calculer la proportion de galette reçue par chacun.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32[Mod.1 - Cal.1 - Cal.4]
Lina souhaite partager ses 48 billes avec son frère
Naïm et sa sœur Julie. Naïm en reçoit les \frac{3}{8} et Julie les deux cinquièmes de ce qui reste1. Calculer la proportion de billes reçues par Julie.
2. Est‑il vrai que Naïm a reçu moins de billes que Julie ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33[Cal.1 - Cal.4 - Com.1]
On pose x=-\frac{2}{3}, y=\frac{3}{4} et z=\frac{4}{5}.1. Calculer \mathrm{A}=z \times(x-y).
2. a. Calculer \mathrm{B}=y \times z-x \times z.
b. Que peut‑on dire de \mathrm{A} et \mathrm{B} ?
3. a. Calculer \mathrm{C}=\frac{1}{z} \div(x-y).
b. Que peut‑on dire de \mathrm{A} et \mathrm{C} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
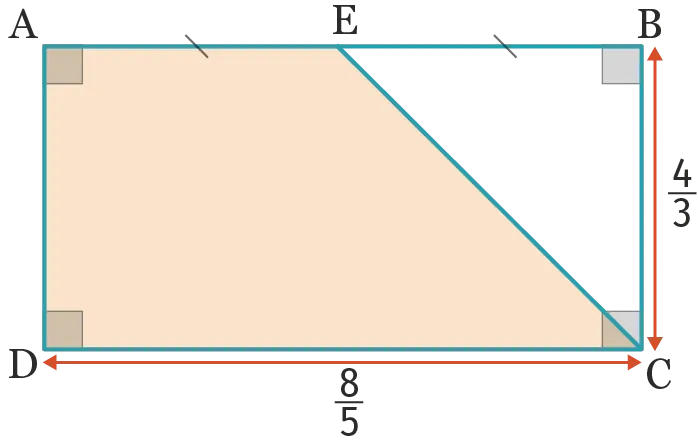
36 [Mod.1 - Cal.1 - Cal.4]
Les longueurs de la figure sont exprimées en cm.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34 [Mod.1 - Cal.1 - Cal.4]
On multiplie deux des trois fractions \frac{-4}{5}, \frac{6}{7} et \frac{2}{9}, puis
on prend l'inverse du résultat.Quelles fractions doit-on choisir pour obtenir le nombre le plus petit possible ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35 [Cal.1 - Cal.4]
On considère le programme de calcul ci-dessous.
\boxed{
\begin{array} { r|l }
1 & \text{Choisir un nombre} \\
2 & \text{Le multiplier par}~\frac{7}{4}\\
3 & \text{Prendre l'inverse du résultat}\\
4 & \text{Le diviser par}~\frac{4}{7}
\end{array}
}
1. Vérifier que si l'on choisit \frac{4}{5} au départ, on obtient \frac{5}{4}.
2. Qu'obtient-on en sortie de programme si on choisit -\frac{7}{8} au départ ?
3. Que peut‑on conjecturer sur le résultat donné par ce programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

