Chapitre 14
Exercices d'entraînement
Géométrie dans l'espace
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer le volume d'une pyramide ou d'un cône de révolution
Propriétés :
1. \text { Volume }{ }_{\text {pyramide }}=\frac{\text { aire de la base } \times \text { hauteur }}{3} .
2. \text { Volume }_{\text {cône }}=\frac{\text { aire de la base } \times \text { hauteur }}{3}=\frac{\pi \times \text { rayon }^{2} \times \text { hauteur }}{3} .
Exemples :
1. Pour calculer le volume d'une pyramide de base d'aire 36 cm2 et de hauteur 10 cm, on écrit \text { Volume }_{\text {pyramide }}=\frac{36 \times 10}{3}=120. Le volume de la pyramide vaut donc 120 cm3.
2. Pour calculer le volume d'un cône de révolution dont la base a pour rayon 5 cm et dont la hauteur est de 12 cm, on écrit \text { Volume }_{\text {cône }}=\frac{\pi \times 5^{2} \times 12}{3}=100 \pi. Le volume du cône vaut donc 100 \pi cm3.
Retrouvez et .
Ressource affichée de l'autre côté.
Faites d�éfiler pour voir la suite.
Faites d�éfiler pour voir la suite.
16[Cal.5 - Rep.7]
1. Calculer, au cm3 près, le volume de cette pyramide.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17[Ch.1 - Rep.5 - Rep.7 - Cal.5]
Pour chaque pyramide, surligner sur la figure les informations utiles pour calculer son volume, puis en donner une valeur arrondie au dixième près.1.

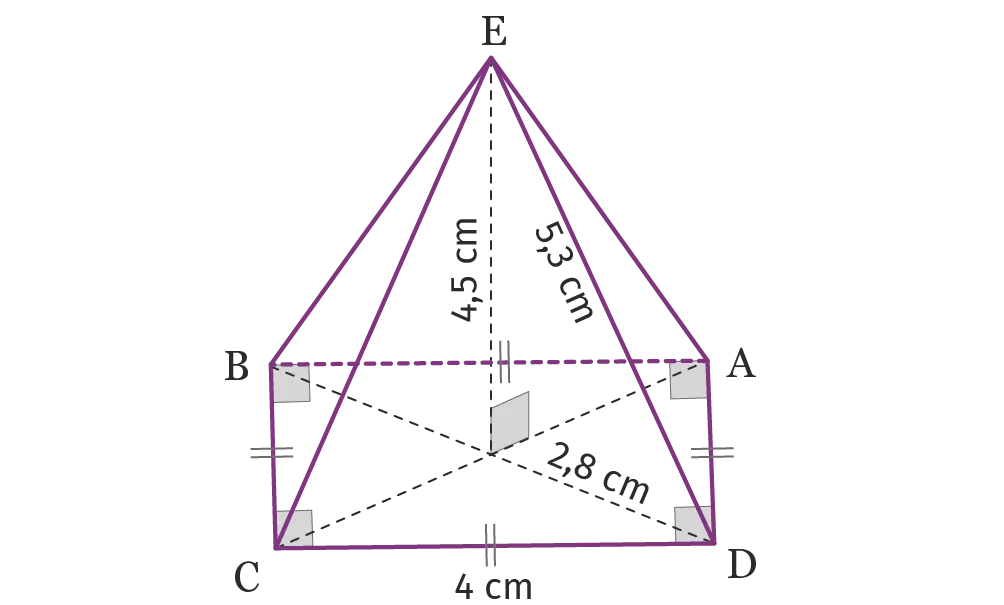

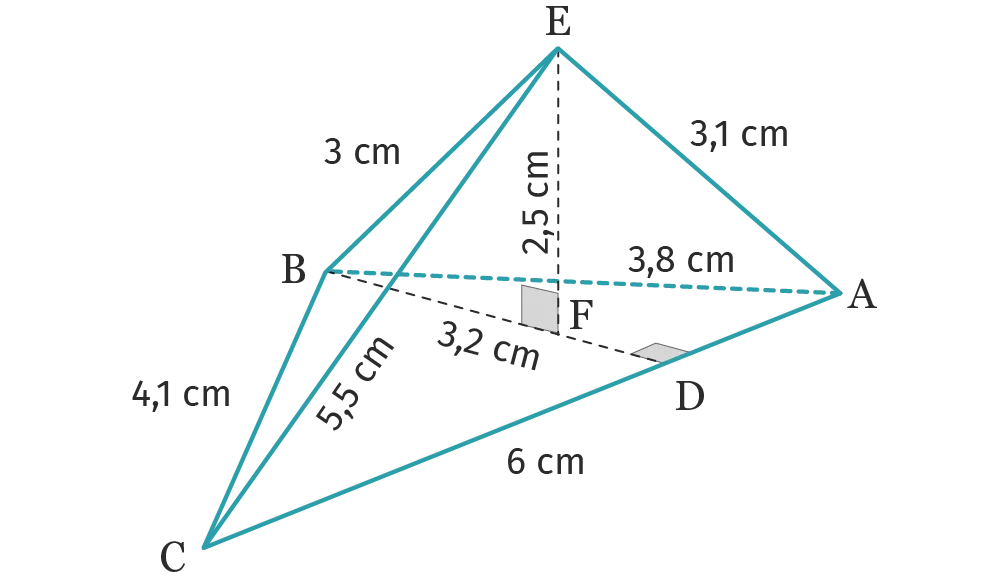
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18[Ch.1 - Cal.5 - Rep.7]
Calculer le volume de ces deux cônes de révolution. Donner la valeur exacte, puis une valeur approchée arrondie au cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19[Rep.7 - Cal.3]
Soit \text{ABCDEFGH} un cube d'arête 6 cm.Calculer le volume de la pyramide \text{EABCD}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Copie d'élève[Rais.5]
Le professeur de Jeanne demande de calculer le volume d'un cône de révolution dont la hauteur mesure 9 cm et dont la base est un cercle de rayon 5 cm.Voici la copie de Jeanne.
Calcul de l'aire de la base : \pi \times 5 \times 2=10 \pi.
Calcul du volume du cône de révolution : \frac{10 \pi \times 9}{3}=30 \pi \approx 94 .
Le cône a un volume environ égal à 94 cm.
Calcul du volume du cône de révolution : \frac{10 \pi \times 9}{3}=30 \pi \approx 94 .
Le cône a un volume environ égal à 94 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 2 \mathrm{~m}^{3}= \mathrm{cm}^{3}
2. 430 \mathrm{~mm}^{3}= \mathrm{cm}^{3}
2. 430 \mathrm{~mm}^{3}=
3. 590~700~ \mathrm{dm}^{3}= \mathrm{m}^{3}
4. 7~600 \mathrm{~cm}^{3}= \mathrm{m}^{3}
4. 7~600 \mathrm{~cm}^{3}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le coin des experts
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Une parfumerie vend des parfums dont les flacons ont une forme particulière.
Le bouchon est une pyramide à base carrée posée sur le flacon, le tout formant une grande pyramide à base carrée.


La hauteur du bouchon vaut \text{3,5} cm et les côtés de sa base mesurent \text{3} cm.
La hauteur de la grande pyramide vaut \text{7,2} cm et les côtés de sa base mesurent \text{8} cm.
On fait l'hypothèse que le flacon est entièrement rempli. Calculer le volume de parfum contenu dans ce flacon en mL. On arrondira au dixième de mL.
La hauteur de la grande pyramide vaut \text{7,2} cm et les côtés de sa base mesurent \text{8} cm.
On fait l'hypothèse que le flacon est entièrement rempli. Calculer le volume de parfum contenu dans ce flacon en mL. On arrondira au dixième de mL.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

