Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 8
Cours 2
Coefficient directeur et équation réduite
11 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ACoefficient directeur d'une droite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Une droite d d'équation ax + by + c = 0 où b \neq 0 possède un vecteur directeur de coordonnées (1\:;m) avec m = -\dfrac{a}{b}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Une droite non parallèle à l'axe des ordonnées a une équation cartésienne de la forme ax + by + c = 0 avec b \neq 0.
Alors le vecteur \vec { u } ( - b\: ; a ) est un vecteur directeur de la droite d.
Le vecteur \dfrac { 1 } { - b } \vec { u } de coordonnées \left( 1\: ; \dfrac { a } { - b } \right) est colinéaire à \vec { u } ( - b\: ; a ), donc c'est un vecteur directeur de la droite d.
Le nombre m vaut -\dfrac { a } { b }.
Alors le vecteur \vec { u } ( - b\: ; a ) est un vecteur directeur de la droite d.
Le vecteur \dfrac { 1 } { - b } \vec { u } de coordonnées \left( 1\: ; \dfrac { a } { - b } \right) est colinéaire à \vec { u } ( - b\: ; a ), donc c'est un vecteur directeur de la droite d.
Le nombre m vaut -\dfrac { a } { b }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Le nombre m s'appelle coefficient directeur de la droite d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La droite d d'équation 3x + 2y - 11 = 0 a pour vecteur directeur (1 \:; - 1\text{,}5) donc son coefficient directeur est -1\text{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
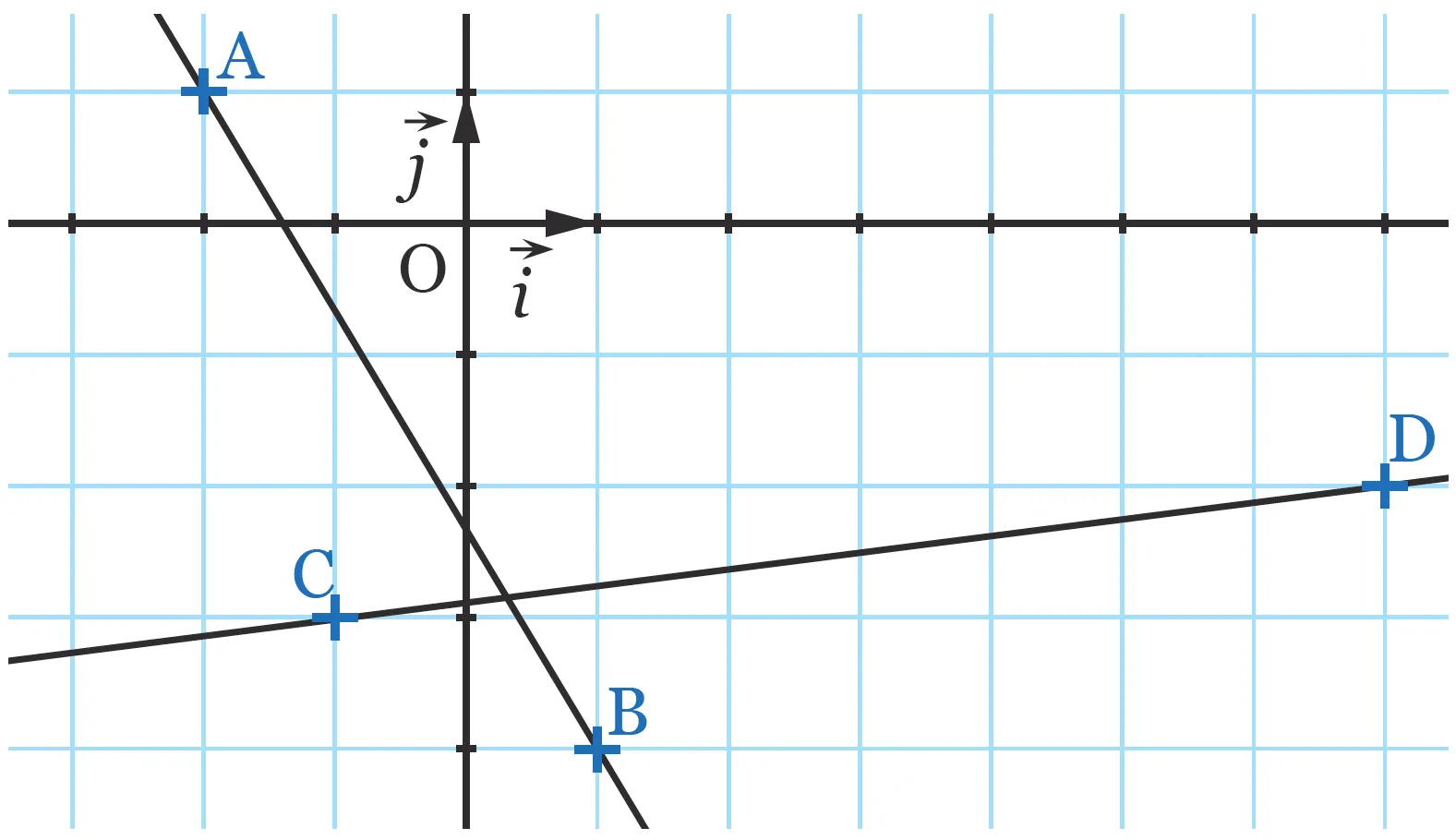
Déterminer graphiquement le coefficient directeur des droites (\text{AB}) et (\text{CD}).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On identifie un vecteur directeur \vec{u} de la droite (\text{AB}) puis on cherche le vecteur colinéaire à \vec{u} qui est de la forme (1\:;m).
- Le nombre m est le coefficient directeur de (\text{AB}).
- On trouve le coefficient directeur de (\text{CD}) de la même manière.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
- \overrightarrow { \text{AB} } ( 3\: ; - 5 ) est un vecteur directeur de la droite (\text{AB}) donc le vecteur \left( 1 \:; - \dfrac { 5 } { 3 } \right) en est aussi un.
- Le coefficient directeur de la droite (\text{AB}) vaut donc - \dfrac { 5 } { 3 }.
- \overrightarrow { \mathrm { CD } } ( 8 \:; 1 ) est un vecteur directeur de la droite (\text{CD}) donc le vecteur \left( 1 \:; \dfrac { 1 } { 8 } \right) en est aussi un. Donc le coefficient directeur de la droite (\text{CD}) vaut \dfrac{1}{8}.
Pour s'entraîner
Exercices et p. 227
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BÉquation réduite d'une droite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Soit une droite d de coefficient directeur m. Il existe un unique nombre p tel que l'équation de d s'écrit y = mx + p .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il existe une seule équation réduite d'une droite car il n'y a qu'un vecteur directeur de la forme (1 \:; m).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Si (1\: ; m) est un vecteur directeur de la droite d, alors son équation cartésienne (de la forme ax + by + c = 0) s'écrit mx - y + k = 0 soit y = mx + k , où k est un nombre réel. Le nombre k est le nombre p cherché.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La droite d'équation y = mx + p coupe l'axe des ordonnées en p.
C'est pour cela que le nombre p s'appelle ordonnée à l'origine de la droite d .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
L'équation y = mx + p s'appelle équation réduite de la droite d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Le coefficient directeur d'une droite (\text{AB}) non parallèle à l'axe des ordonnées est égal à \dfrac { y _ { \mathrm { B } } - y _ { \mathrm { A } } } { x _ { \mathrm { B } } - x _ { \mathrm { A } } }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On a aussi m = \dfrac { y _ { \mathrm { A } } - y _ { \mathrm { B } } } { x _ { \mathrm { A } } - x _ { \mathrm { B } } }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Soient \text{A} et \text{B} deux points disctincts. Le vecteur \overrightarrow { \mathrm { AB } } \left( x _ { \mathrm { B } } - x _ { \mathrm { A } } \:; y _ { \mathrm { B } } - y _ { \mathrm { A } } \right) est un vecteur directeur de la droite (\text{AB}), donc le vecteur \dfrac { 1 } { x _ { \mathrm { B } } - x _ { \mathrm { A } } } \overrightarrow { \mathrm { AB } } aussi car x _ { \mathrm { B } } - x _ { \mathrm { A } } \neq 0 : ses coordonnées sont \left( 1\: ; \dfrac { y _ { \mathrm { B } } - y _ { \mathrm { A } } } { x _ { \mathrm { B } } - x _ { \mathrm { A } } } \right).
On a donc m = \dfrac { y _ { \mathrm { B } } - y _ { \mathrm { A } } } { x _ { \mathrm { B } } - x _ { \mathrm { A } } }.
On a donc m = \dfrac { y _ { \mathrm { B } } - y _ { \mathrm { A } } } { x _ { \mathrm { B } } - x _ { \mathrm { A } } }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut associer une équation réduite à une fonction affine. Lorsque m \gt 0, la fonction est croissante. Lorsque m = 0 , elle est constante et lorsque m \lt 0, elle est décroissante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le coefficient directeur de la droite passant par \text{A}(1 \:; 3) et \text{B}(4\: ; 5) est m=\dfrac{2}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Déterminer l'équation réduite de la droite passant par les points \text{A}(-4\: ; 4) et \text{B}(3\: ; 0).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On commence par calculer le coefficient directeur.
- On utilise ensuite les coordonnées d'un des deux points pour calculer l'ordonnée à l'origine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
- Le coefficient directeur de la droite (\mathrm { AB }) vaut \dfrac { y _ { \mathrm { B } } - y _ { \mathrm { A } } } { x _ { \mathrm { B } } - x _ { \mathrm { A } } } = \dfrac { 0 - 4 } { 3 - ( - 4 ) } = - \dfrac { 4 } { 7 }.
- Comme B appartient à la droite (\mathrm { AB }), ses coordonnées vérifient l'équation y = - \dfrac { 4 } { 7 } x + p : 0 = - \dfrac { 4 } { 7 } \times 3 + p donc p = \dfrac { 12 } { 7 }.
Donc l'équation réduite de la droite (\mathrm { AB }) s'écrit y = - \dfrac { 4 } { 7 } x + p avec p à déterminer.
La droite (\mathrm { AB }) a donc pour équation réduite y = - \dfrac { 4 } { 7 } x + \dfrac { 12 } { 7 }.
Pour s'entrainer
Exercices p. 227, p. 231 et p. 232
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah