Chapitre 8
Cours 1
Vecteurs directeurs et équations cartésiennes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans tout ce chapitre, on se place dans un repère orthonormé (\text{O} ; \vec{i} , \vec{j}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AVecteur directeur d'une droite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
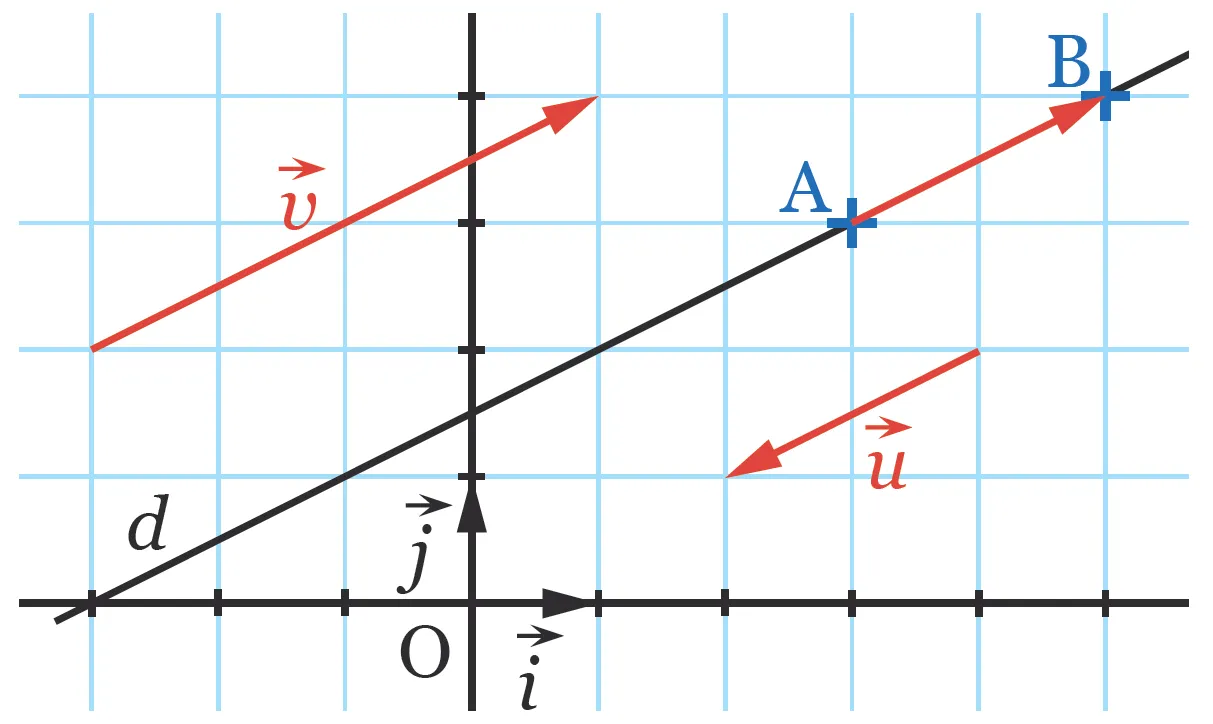
On appelle vecteur directeur d'une droite d tout représentant du vecteur \overrightarrow{\text{AB}} où \text{A} et \text{B} sont deux points quelconques distincts de la droite d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une droite possède une infinité de vecteurs directeurs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soient trois points \text{A}(1\:; 5) , \text{B}(-3\: ; 2) et \text{C}(2 \:; - 1) dans un repère orthonormé.
1. Déterminer un vecteur directeur de la droite (\text{BC}).
2. Détailler la construction de la parallèle à (\text{BC}) passant par (\text{A}).
1. Déterminer un vecteur directeur de la droite (\text{BC}).
2. Détailler la construction de la parallèle à (\text{BC}) passant par (\text{A}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On calcule les coordonnées d'un vecteur directeur de la droite.
2. La droite (\text{BC}) et sa parallèle ont les mêmes vecteurs directeurs, il suffit d'en prendre un représentant d'origine \text{A}.
2. La droite (\text{BC}) et sa parallèle ont les mêmes vecteurs directeurs, il suffit d'en prendre un représentant d'origine \text{A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. Le vecteur \overrightarrow{\text{BC}}(5 \:; - 3) est un vecteur directeur de la droite (\text{BC}).
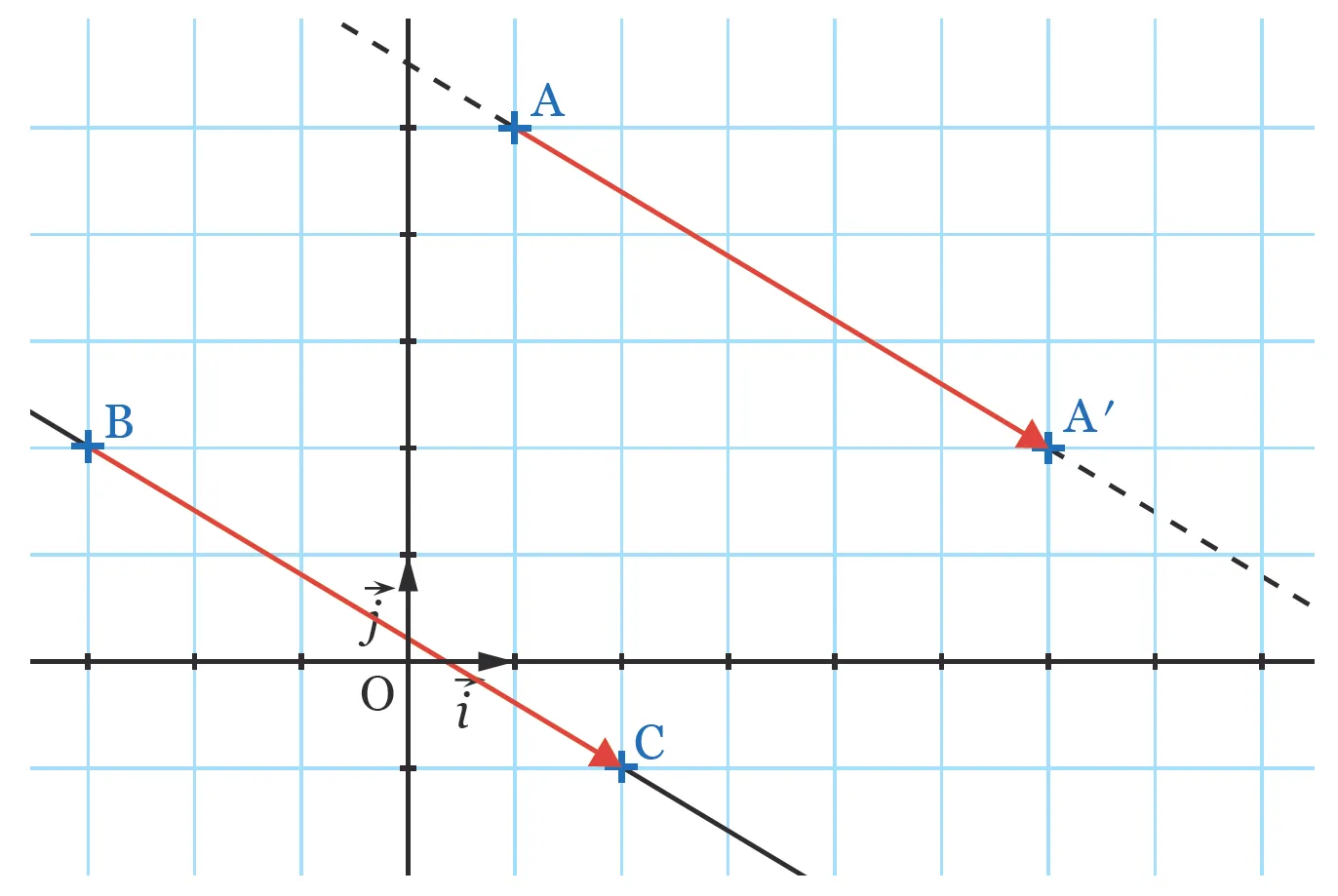
2. Le vecteur \overrightarrow{\text{BC}}(5\: ; - 3) est également un vecteur directeur de la parallèle à (\text{BC}) passant par \text{A}. On construit le point \text{A}' tel que \overrightarrow{\text{AA}'} = \overrightarrow{\text{BC}}. Ainsi, x_{\text{A}'} - x_{\text{A}} = x_{\text{C}} - x_{\text{B}} d'où x_{\text{A}'} = x_{\text{C}} - x_{\text{B}} + x_{\text{A}} = 2 -(-3) + 1 = 6.
De même, on calcule y_{\text{A}'} = y_{\text{C}} - y_{\text{B}} + y_{\text{A}} = 2. On trouve \text{A}'(6\: ; 2). La droite (\text{AA}') est la droite cherchée.
2. Le vecteur \overrightarrow{\text{BC}}(5\: ; - 3) est également un vecteur directeur de la parallèle à (\text{BC}) passant par \text{A}. On construit le point \text{A}' tel que \overrightarrow{\text{AA}'} = \overrightarrow{\text{BC}}. Ainsi, x_{\text{A}'} - x_{\text{A}} = x_{\text{C}} - x_{\text{B}} d'où x_{\text{A}'} = x_{\text{C}} - x_{\text{B}} + x_{\text{A}} = 2 -(-3) + 1 = 6.
De même, on calcule y_{\text{A}'} = y_{\text{C}} - y_{\text{B}} + y_{\text{A}} = 2. On trouve \text{A}'(6\: ; 2). La droite (\text{AA}') est la droite cherchée.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BÉquation cartésienne de droite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Dans un repère orthonormé, les coordonnées de l'ensemble des points \text{M}(x \:; y) d'une droite vérifient une relation ax + by + c = 0 , où a, b et c sont des nombres réels.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Si a=0 et b \neq 0 alors y = - \dfrac { c } { b } et la droite est parallèle à l'axe des abscisses.
Si b=0 et a \neq 0 alors x = - \dfrac { c } { a } et la droite est parallèle à l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Soient \mathrm { P } \left( x _ { \mathrm { P } } \:; y _ { \mathrm {P } } \right) et \mathrm { Q } \left( x _ { \mathrm { Q } } \:; y _ { \mathrm { Q } } \right) deux points de d.
Alors, pour tout point \mathrm { M } ( x \:; y ) appartenant à d :
\overrightarrow { \mathrm { PM } } \left( x - x _ { \mathrm{ P }} \:; y - y _ { \mathrm{ P }} \right) et \overrightarrow { \mathrm { PQ } } \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } }\: ; y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) sont colinéaires.
On a donc \det ( \overrightarrow { \text{PM} }\: ; \overrightarrow { \text{PQ} } ) = 0
c'est-à-dire \left( x - x _ { \mathrm { P } } \right) \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) - \left( y - y _ { \mathrm { P } } \right) \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) = 0.
Donc x \left( y _ { \mathrm{Q} } - y _ { \mathrm { P } } \right) - x _ { \mathrm { P } } \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) - y \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) + y _ { \mathrm { P } } \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) = 0.
Donc \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) x + \left( x _ { \mathrm { P } } - x _ { \mathrm { Q } } \right) y + \left( y _ { \mathrm { P } } x _ { \mathrm { Q } } - x _ { \mathrm { P } } y _ { \mathrm { Q } } \right) = 0.
En posant a = y _ { \mathrm { Q } } - y _ { \mathrm { P } }, b = x _ { \mathrm { p } } - x _ { \mathrm { Q } }, et c = x _ { \mathrm{Q} } y _ { \mathrm { P } } - x _ { \mathrm { P } } y _ { \mathrm { Q } } on a donc a x + b y + c = 0.
Alors, pour tout point \mathrm { M } ( x \:; y ) appartenant à d :
\overrightarrow { \mathrm { PM } } \left( x - x _ { \mathrm{ P }} \:; y - y _ { \mathrm{ P }} \right) et \overrightarrow { \mathrm { PQ } } \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } }\: ; y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) sont colinéaires.
On a donc \det ( \overrightarrow { \text{PM} }\: ; \overrightarrow { \text{PQ} } ) = 0
c'est-à-dire \left( x - x _ { \mathrm { P } } \right) \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) - \left( y - y _ { \mathrm { P } } \right) \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) = 0.
Donc x \left( y _ { \mathrm{Q} } - y _ { \mathrm { P } } \right) - x _ { \mathrm { P } } \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) - y \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) + y _ { \mathrm { P } } \left( x _ { \mathrm { Q } } - x _ { \mathrm { P } } \right) = 0.
Donc \left( y _ { \mathrm { Q } } - y _ { \mathrm { P } } \right) x + \left( x _ { \mathrm { P } } - x _ { \mathrm { Q } } \right) y + \left( y _ { \mathrm { P } } x _ { \mathrm { Q } } - x _ { \mathrm { P } } y _ { \mathrm { Q } } \right) = 0.
En posant a = y _ { \mathrm { Q } } - y _ { \mathrm { P } }, b = x _ { \mathrm { p } } - x _ { \mathrm { Q } }, et c = x _ { \mathrm{Q} } y _ { \mathrm { P } } - x _ { \mathrm { P } } y _ { \mathrm { Q } } on a donc a x + b y + c = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
La relation ax + by + c = 0 s'appelle équation cartésienne de la droite d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il existe une infinité d'équations cartésiennes d'une même droite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Le vecteur (-b\: ; a) est un vecteur directeur de la droite d'équation ax + by + c = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réciproquement, si le vecteur (-b \:; a) est un vecteur directeur de d, alors une équation cartésienne de d est ax + by + c = 0 (avec c à déterminer).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Voir .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Si la droite d a pour équation 5x+4y-11=0, alors le vecteur \overrightarrow{u}\left(-4;5\right) est un vecteur directeur de cette droite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Déplacer les points \mathrm{A} et \mathrm{B} pour modifier la droite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Déterminer une équation cartésienne de la droite passant par \text{A}(2\: ; 1) et \text{B}(7\: ; 3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On calcule les coordonnées des vecteurs \overrightarrow{\text{AB}} et \overrightarrow{\text{AM}}.
2. On utilise le déterminant xy' - x 'y de ces deux vecteurs. Ce déterminant est nul lorsque les points \text{A}, \text{B} et \text{M} sont alignés.
3. On développe et on réduit l'expression pour obtenir la forme d'une équation cartésienne.
2. On utilise le déterminant xy' - x 'y de ces deux vecteurs. Ce déterminant est nul lorsque les points \text{A}, \text{B} et \text{M} sont alignés.
3. On développe et on réduit l'expression pour obtenir la forme d'une équation cartésienne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Pour tout point \text{M}(x \:; y) de la droite (\text{AB}), \overrightarrow{\text{AM}} et \overrightarrow{\text{AB}} sont colinéaires. Les coordonnées de ces vecteurs sont \overrightarrow{\text{AM}}(x-2\:;y-1) et \overrightarrow{\text{AB}}(5\:;2).
Le déterminant de ces deux vecteurs est nul, donc on a : (x - 2) \times 2 - 5(y - 1) = 0 soit 2x - 4 - 5y + 5 = 0 d'où 2x - 5y + 1 = 0 .
Exercices et p. 227, et p. 229
Le déterminant de ces deux vecteurs est nul, donc on a : (x - 2) \times 2 - 5(y - 1) = 0 soit 2x - 4 - 5y + 5 = 0 d'où 2x - 5y + 1 = 0 .
Pour s'entraîner
Exercices et p. 227, et p. 229
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

