Sommaire
Mes pages
N° Page
Ouverture
p. 1-11
Fonctions
Géométrie
Testez le chapitre 100 % débloqué
Statistiques et probabilités
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 339
Vue papier
Animation montrant le basculement entre la vue numérique et la vue papier
Découvrez la vue papier en cliquant ici
Page précédente
Exclu. numérique 2023
Chapitre 8

Équations de droites

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exclu. numérique 2023

Vidéo « À quoi ça sert les maths ? »

poster de la vidéo
00:00 / --:--
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour Photographie d'architecture moderne: structure géométrique avec lignes bleues et blanches reflétant le ciel.Photographie d'architecture moderne: structure géométrique avec lignes bleues et blanches reflétant le ciel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Capacités attendues

1. Déterminer une équation de droite.
2. Déterminer la pente ou un vecteur directeur d'une droite donnée par une équation ou une représentation graphique.
3. Tracer une droite connaissant une équation cartésienne ou réduite.
4. Établir si trois points sont alignés ou non.
5. Déterminer si deux droites sont parallèles ou sécantes.
6. Déterminer le point d'intersection de deux droites sécantes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
L'architecture utilise une grande variété de formes géométriques pour exprimer des volumes. La ligne droite est un outil privilégié, tant en intérieur pour donner une impression d'espace, qu'en extérieur pour harmoniser un ensemble.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Avant de commencer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Prérequis

1. Savoir étudier la position relative de deux droites dans le plan.
2. Connaître les notions de vecteur et de repérage dans le plan.
3. Savoir calculer le déterminant de deux vecteurs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Anecdote

En géométrie projective, deux droites d'un plan sont toujours sécantes.
Placeholder pour Route asphaltée traversant champs de colza, perspective linéaire vers horizon bleu. Paysage printanier.Route asphaltée traversant champs de colza, perspective linéaire vers horizon bleu. Paysage printanier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Démontrer que des droites sont parallèles

On munit le plan d'un repère orthonormé ( \mathrm { O } ; \vec { i } , \vec { j } ). On considère le quadrilatère \mathrm { ABCD } dans ce repère tel que \mathrm{A} ( - 3 \,; 1 ), \mathrm{B} ( 1\,; 3 ), \mathrm{C} ( 4\, ; 1 ) et \mathrm{D} ( 0\, ; -1 ).
Démontrer que ce quadrilatère est un parallélogramme :
1. en utilisant les vecteurs ;

2. en utilisant des calculs de longueurs ;

3. en utilisant les diagonales.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Lire les coordonnées des vecteurs de la figure.

Lire les coordonnées des vecteurs de la figure.
Lire les coordonnées des vecteurs de la figure
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Calculer des coordonnées de vecteurs

Calculer les coordonnées du vecteur \overrightarrow{\text{AB}} dans chacun des cas suivants :

1. \text{A} ( - 1\,; 1 ) et \text{B} ( 4\,; - 3 )

2. \mathrm { A } \left( \dfrac { 2 } { 3 }\,; \dfrac { 1 } { 9 } \right) et \mathrm { B } \left( 1\,; - \dfrac { 8 } { 9 } \right)

3. \mathrm {A} ( - 0\text{,}6\,; 1\text{,}1 ) et \mathrm { B } ( 0\text{,}6\,; 0\text{,}7 )
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Calculer le déterminant de deux vecteurs

Calculer le déterminant des vecteurs \vec{u} et \vec{v} dans chacun des cas suivants :
1. \vec { u } ( - 3\,; 1 ) et \vec { v } ( 2\,; 2 )

2. \vec { u } ( 3\,; 8 ) et \vec { v } ( - 9;\, - 24 )

3. \vec { u } ( 4\,; - 7 ) et \vec { v } ( 0\,; - 7 )

4. \vec { u } ( - 0\text{,}4\,; 1\text{,}1 ) et \vec { v } ( 8\text{,}6\,; - 1\text{,}6 )

5. \vec { u } \left( \dfrac { 1 } { 2 }\,; \dfrac { 5 } { 4 } \right) et \vec { v } \left( - \dfrac { 1 } { 4 }\,; \dfrac { 3 } { 4 } \right)

6. \vec { u } \left( - \dfrac { 2 } { 3 } \,; \dfrac { 3 } { 2 } \right) et \vec { v } \left( \dfrac { 1 } { 6 } \,; \dfrac { 3 } { 4 } \right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Tester la colinéarité de vecteurs

Parmi les vecteurs \vec { u } ( - 6\, ; 1\text{,}5 ) , \vec { v } ( 3\,; - 2 ) et \vec { w } ( 4\, ; - 1 ), quels sont les deux vecteurs colinéaires ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Problème

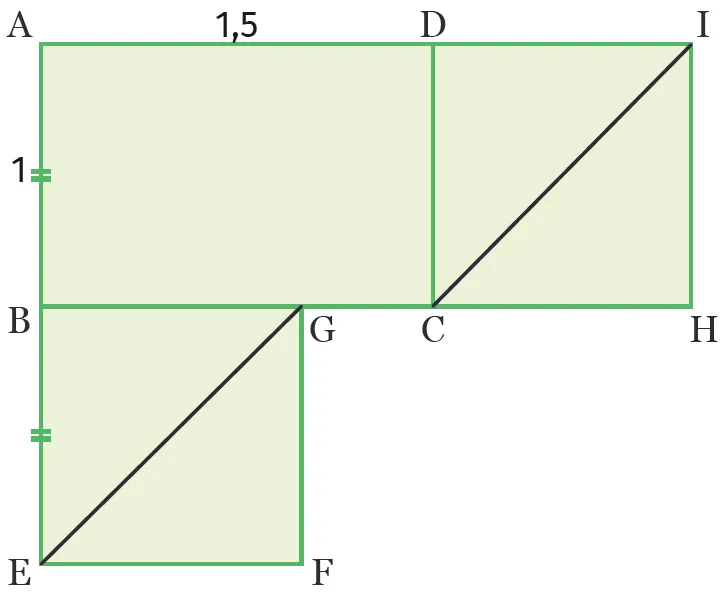
\text{ABCD} est un rectangle de longueur 1,5 et de largeur 1. \text{B} est le milieu de [\text{AE}]. \text{BEFG} et \text{DCHI } sont des carrés. On se place dans le repère ( \mathrm { B } ; \overrightarrow { \mathrm { BG } } , \overrightarrow { \mathrm { BA } } ).
1. Donner les coordonnées de tous les points de la figure.

2. Démontrer que les droites ( \mathrm { EG }) et (\mathrm{CI}) sont parallèles.

3. Les points \mathrm { I }, \mathrm { C } et \mathrm { F } sont-ils alignés ? Justifier par le calcul.


Placeholder pour Schéma géométrique: deux rectangles, diagonale reliant coins opposés. Équations de droites.Schéma géométrique: deux rectangles, diagonale reliant coins opposés. Équations de droites.
Page suivante