Chapitre 8
Synthèse
Exercices de synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
89
[Calculer.]
Les points \text{I}, \text{J} et \text{K} sont les milieux des côtés [ \mathrm { AB } ], [ \mathrm { AC } ] et [ \mathrm { BC } ].

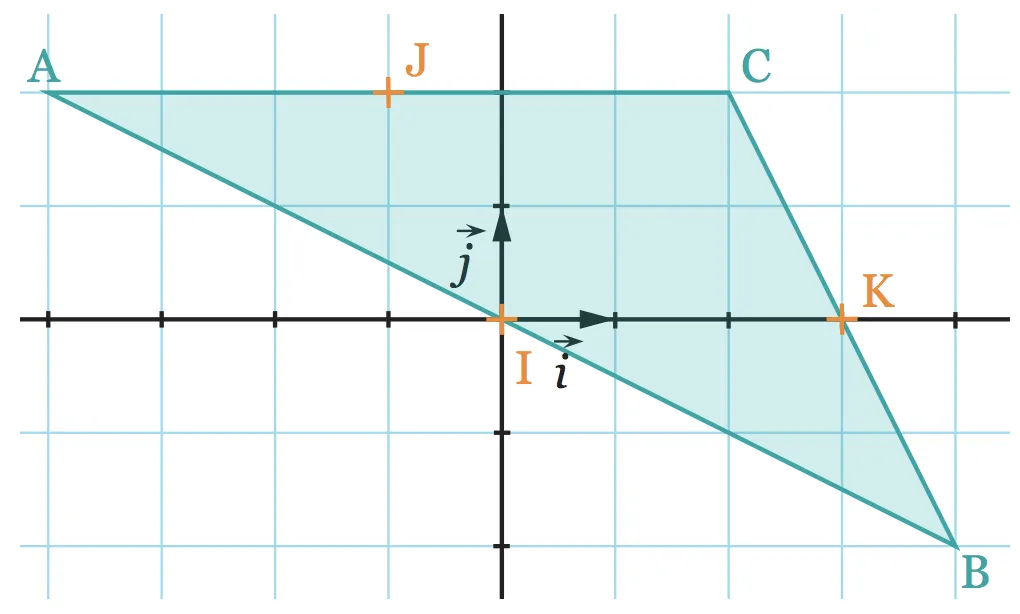


1. Déterminer les équations réduites des droites ( \mathrm { AK } ) et ( \mathrm { BJ } ).
2. En déduire les coordonnées de leur point d'intersection \mathrm {G}.
3. Démontrer que \mathrm{G} appartient aussi à la droite ( \mathrm{ CI } ).
2. En déduire les coordonnées de leur point d'intersection \mathrm {G}.
3. Démontrer que \mathrm{G} appartient aussi à la droite ( \mathrm{ CI } ).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
90
[Chercher.]
On a représenté dans le repère ci-dessous une maison vue de côté. L'unité est le mètre.
Les coordonnées des points représentés sont les suivantes : \mathrm { A } ( 1\: ; 0 ) , \mathrm { B } ( 1\: ; 4 ) , \mathrm { C } ( 3\: ; 5\text{,} 5 ) , \mathrm { E } ( 4\: ; 5\text{,} 5 ) , \mathrm { F } ( 7\: ; 4 ) et \mathrm { G } ( 7\: ; 0 ). Le point \text{D} est à l'intersection des droites ( \mathrm{BC} ) et ( \mathrm { EF } ).

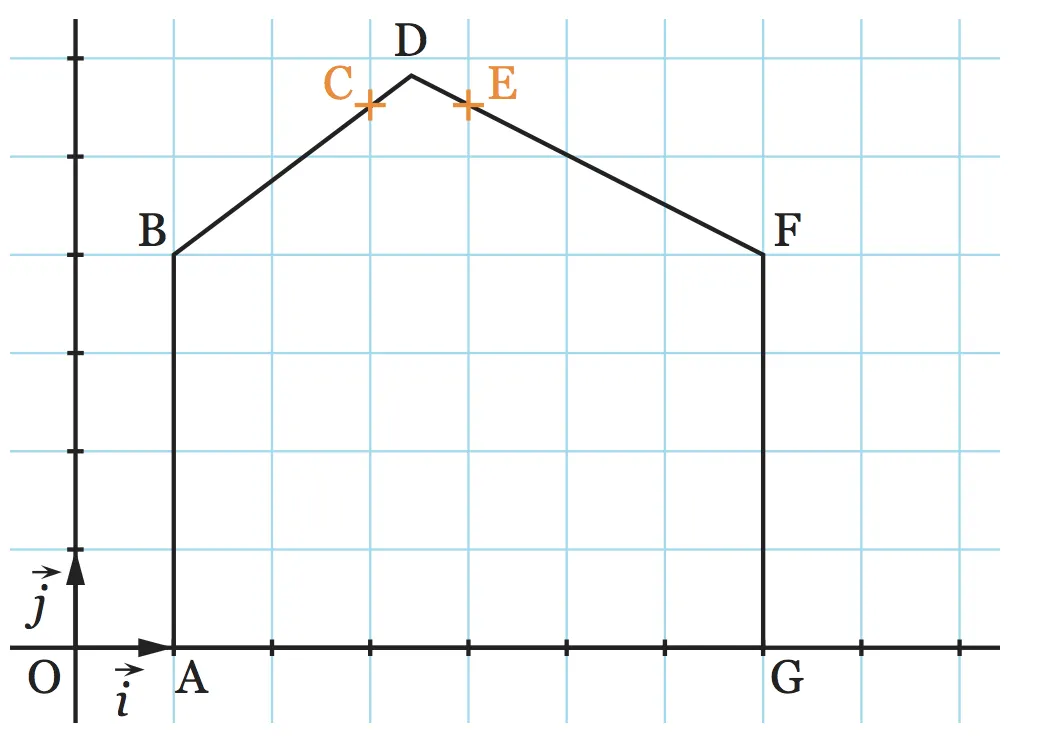
Les coordonnées des points représentés sont les suivantes : \mathrm { A } ( 1\: ; 0 ) , \mathrm { B } ( 1\: ; 4 ) , \mathrm { C } ( 3\: ; 5\text{,} 5 ) , \mathrm { E } ( 4\: ; 5\text{,} 5 ) , \mathrm { F } ( 7\: ; 4 ) et \mathrm { G } ( 7\: ; 0 ). Le point \text{D} est à l'intersection des droites ( \mathrm{BC} ) et ( \mathrm { EF } ).


1. Calculer la pente de la partie gauche du toit.
2. Calculer la pente de la partie droite du toit.
3. En déduire les coordonnées du point \mathrm{D}.
2. Calculer la pente de la partie droite du toit.
3. En déduire les coordonnées du point \mathrm{D}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
91
[Calculer.]
Dans le repère ci-dessous, \mathrm{I} est le milieu du segment [ \mathrm { AB } ].

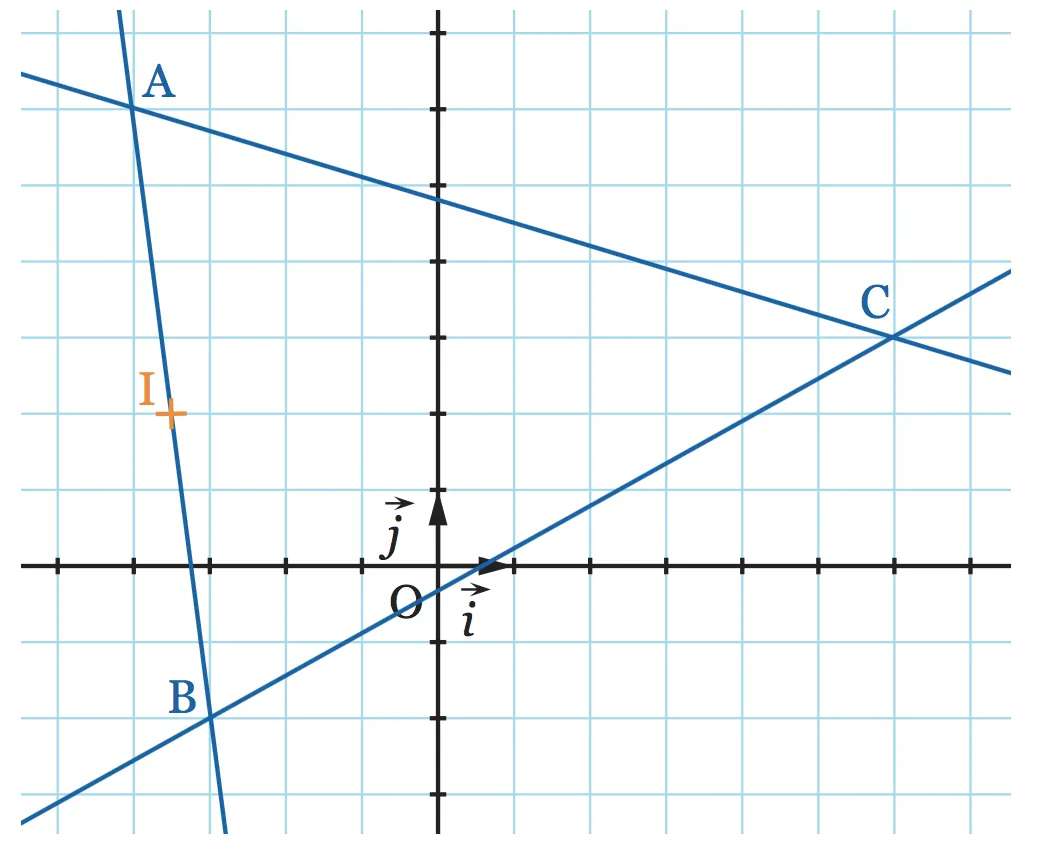


1. Déterminer une équation de chacune des droites ( \mathrm { AC } ) et ( \mathrm { BC } ).
2. Déterminer une équation de la droite \Delta parallèle à \mathrm{(BC)} passant par \mathrm{I}.
3. Calculer les coordonnées du point d'intersection \mathrm{J} des droites \Delta et ( \mathrm { AC } ). Que représente ce point pour le segment [ \mathrm { AC } ] ? Justifier.
2. Déterminer une équation de la droite \Delta parallèle à \mathrm{(BC)} passant par \mathrm{I}.
3. Calculer les coordonnées du point d'intersection \mathrm{J} des droites \Delta et ( \mathrm { AC } ). Que représente ce point pour le segment [ \mathrm { AC } ] ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
92
[Représenter.]
Paul achète un arbuste qui mesure 75 cm. L'horticulteur lui dit qu'avec un arrosage régulier, sa plante gagnera 5 mm à la fin d'une journée en moyenne. On admet que la croissance se fait de façon continue tout au long de la journée.
1. Représenter dans un repère bien choisi l'évolution de la taille de la plante.
2. Une autre plante, plus petite mais vivace, mesurait 60 cm lorsque Paul l'a achetée, et grandira de 8 mm par jour en moyenne. Combien de temps faudra-t-il à cette plante pour atteindre la même taille que l'autre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
93
[Calculer.]
On souhaite déterminer par le calcul les coefficients m et p de l'équation réduite y = mx + p de la droite \mathrm{(AB)} dans le cas général. Pour cela, on note \left( x _ { \mathrm { A } }\: ; y _ { \mathrm { A } } \right) les coordonnées de \mathrm { A } et \left( x _ { \mathrm { B } } \:; y _ { \mathrm { B } } \right) les coordonnées de \mathrm{B} , avec x _ { \mathrm { A } } \neq x _ { \mathrm { B } } .
1. Montrer que cela revient à résoudre le système d'inconnues m et p suivant :
\text { (S) } \begin{cases} { m x _ { \mathrm { A } } + p = y _ { \mathrm { A } } } \\ { m x _ { \mathrm { B } } + p = y _ { \mathrm { B } } } \end{cases}
2. En déduire l'expression de m et p en fonction des coordonnées de \mathrm{A} et \mathrm{B}.
1. Montrer que cela revient à résoudre le système d'inconnues m et p suivant :
\text { (S) } \begin{cases} { m x _ { \mathrm { A } } + p = y _ { \mathrm { A } } } \\ { m x _ { \mathrm { B } } + p = y _ { \mathrm { B } } } \end{cases}
2. En déduire l'expression de m et p en fonction des coordonnées de \mathrm{A} et \mathrm{B}.
3. Programmer sur Python la fonction « Droite (a, b, c et d) » qui donne l'équation réduite d'une droite où a, b, c et d sont les coordonnées de deux points.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
94
En SVT
[Représenter.]
Échanges gazeux.
Un entomologiste étudie les échanges gazeux entre plantes dans une culture sous serre. Il obtient les résultats suivants :
- Une plantation de 80 ficus et 50 caoutchouc relâchent 75 m3 d'\text{O}_2 en une nuit.
- Une plantation de 30 ficus et 60 caoutchouc relâchent 57 m3 d'\text{O}_2 en une nuit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
95
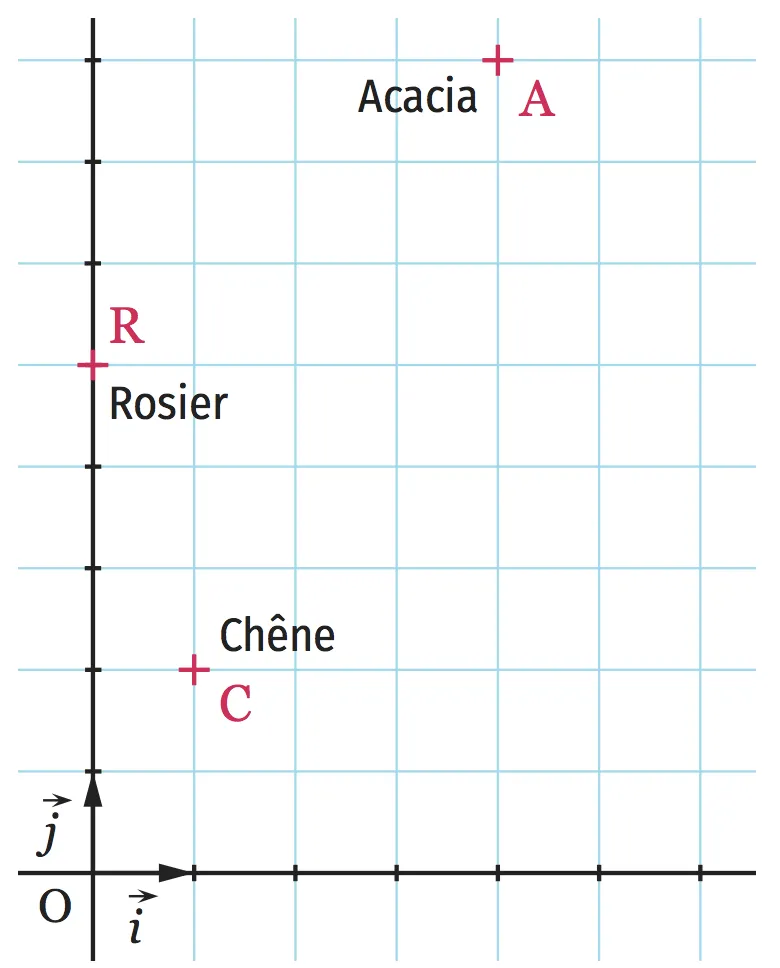
[Chercher.] Aileen organise une chasse au trésor dans son jardin pour l'anniversaire de son petit frère. Elle a creusé un trou et caché des paquets de bonbons. Pour pouvoir aider les amis de son frère, elle dessine un plan de la cachette à l'échelle 1 unité = 1 mètre.
Elle note que le trésor est aligné avec le chêne (appelé \mathrm{C}) et l'acacia (appelé \mathrm{A}), et qu'il est exactement à \sqrt{5} mètres du rosier grimpant (appelé \mathrm{R}).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
96
[Calculer.]
( \mathrm { O } ; \vec { i } , \vec { j } )est un repère orthonormé du plan. On place un point \mathrm{M} sur l'axe des abscisses et un point \mathrm{N} sur l'axe des ordonnées. On appelle \alpha l'abscisse de \mathrm{M} et \beta l'ordonnée de \mathrm{N}. On suppose que \alpha et \beta sont tous les deux non nuls. Soit d et d' les droites d'équation respective x - y + 1 = 0 et y = 2 x.
1. Déterminer, en fonction de \alpha et \beta , une équation cartésienne de la droite ( \mathrm{M N} ).
2. Déterminer une condition sur les réels \alpha et \beta pour que la droite ( \mathrm{M N} ) soit parallèle à la droite d.
3. a. Déterminer une condition sur les réels \alpha et \beta pour que la droite ( \mathrm{M N} ) soit sécante à la droite d'.
b. On suppose 2 \alpha + \beta \neq 0 . Exprimer en fonction de \alpha et \beta les coordonnées du point d'intersection \mathrm{T} des droites ( \mathrm{M N} ) et d'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
97
[Chercher.]
Soit ( \mathrm { O } ; \vec { i } , \vec { j } ) un repère du plan. Soit k un réel et soit d_k la droite d'équation cartésienne 2 k x + ( 1 - k ) y + 3 k - 1 = 0.
1. a. Donner une équation cartésienne de la droite d_0 et la tracer dans le repère.
b. Donner une équation cartésienne de la droite d_1 et la tracer dans le repère.
c. Tracer dans le repère les droites d_{-1}, d_{2} et d_{-2}.
d. Quelle conjecture peut-on émettre pour les droites d_k ?
2. Démontrer que les droites d_k sont concourantes en un point \mathrm{C} dont on calculera les coordonnées.
3. Déterminer les éventuelles valeurs de k pour lesquelles :
a. d_k passe par le point \mathrm{A} ( - 3\: ; - 4 ) ?
b. d_k est parallèle à la droite \Delta d'équation 6x-4y+1=0 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
98
En physique
[Modéliser.]
En optique, on rappelle les règles de construction des rayons lumineux traversant une lentille convergente de foyers \mathrm{F} et \mathrm{F}', et de centre optique \mathrm{O} :
- les rayons passant par le centre optique ne sont pas déviés ;
- les rayons parallèles à l'axe des foyers sortent de la lentille en passant par \mathrm{F}
- les rayons passant par \mathrm{F} sortent de la lentille en passant à l'axe des foyers.
On a : \mathrm{OF} = \mathrm{OF'} = f' ; f' est la distance focale de la lentille.
On choisit le point \mathrm{O} comme origine d'un repère orthonormé, l'axe des abscisses étant la droite (\mathrm{FF'}).

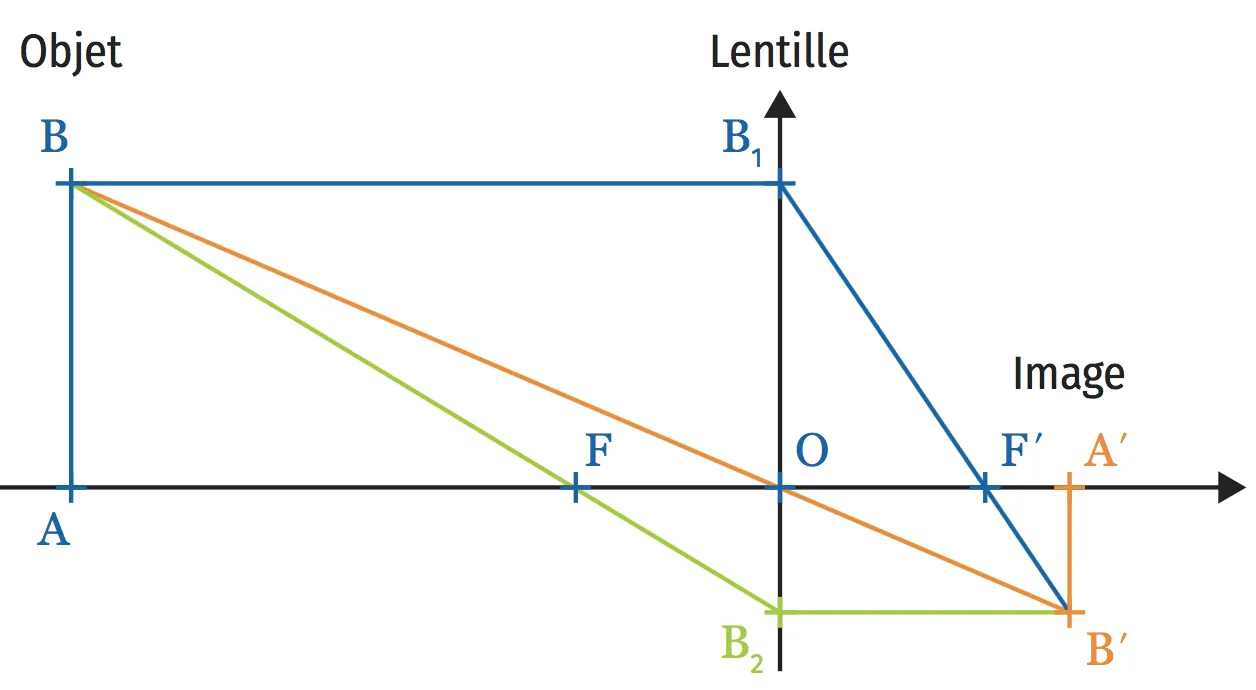


1. Déterminer les coordonnées des foyers \mathrm{F} et \mathrm{F'}.
2. On note x _ { \mathrm { A } } l'abscisse de \mathrm{A} avec x _ { \mathrm { A } } \neq 0 et y _ { \mathrm { B } } l'ordonnée de \mathrm{B} .
a. Déterminer une équation cartésienne de la droite ( \mathrm { OB } ).
b. Déterminer une équation cartésienne de la droite ( \mathrm { BF } ).
3. En déduire les coordonnées des points \mathrm{A'} et \mathrm{B'} en fonction de f' , de x _ { \mathrm { A } } et de y _ { \mathrm { B } } .
4. Retrouver la relation suivante, appelée « relation de conjugaison » : \dfrac { 1 } { x _ { \mathrm { A } } ^ { \prime } } - \dfrac { 1 } { x _ { \mathrm { A } } } = \dfrac { 1 } { f ^ { \prime } }\cdot
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


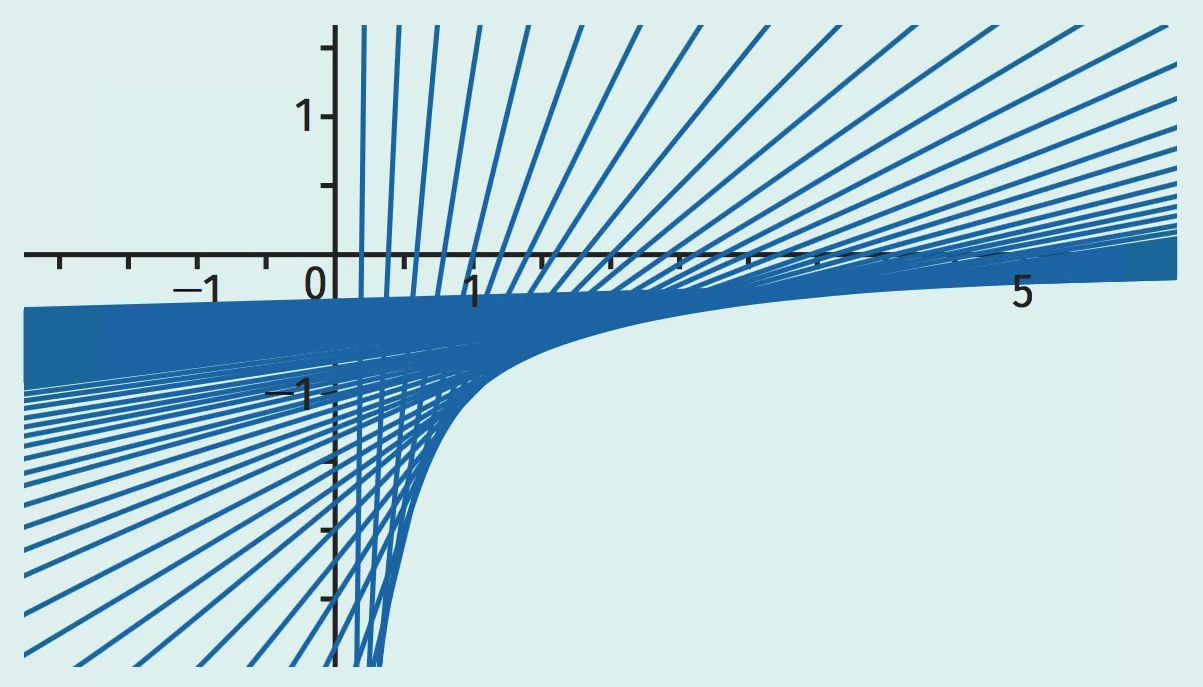
Astronome et mathématicien hollandais du XVIIe siècle, Christiaan Huygens (1629-1695) développa de nouveaux objets lors de ses travaux en optique. En particulier, il étudia les enveloppes de courbes, obtenues en traçant la famille des droites tangentes en chaque point de la courbe. Ici, l'enveloppe de la fonction inverse (sur l'intervalle des réels positifs).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de Maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
99
Défi
On souhaite déterminer le nombre de points à co0rdonnées entières sur une droite dans un intervalle donné.
1. On considère la droite d d'équation y = \dfrac { 3 } { 4 } x + 1.
a. Montrer que le point ( 0 \:; 1 ) appartient à cette droite.
b. Combien y a-t-il de points à coordonnées entières sur la droite pour x variant dans l'intervalle [ - 10 \:; 10 ] ? dans l'intervalle [ 100 \:; 200 ] ?
c. Quelle est l'amplitude minimale d'un intervalle sur lequel on comptera au moins 100 points à coordonnées entières ?
2. Reprendre l'exercice avec la droite d'équation y = \dfrac { 3 } { 4 } x + \dfrac { 1 } { 2 }
3. Reprendre l'exercice avec la droite d'équation y = \dfrac { 3 } { 4 } x + \dfrac { 1 } { 3 }
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
100
Énigme
Un paysan élève des poulets et des lapins. Au total, il y a 50 têtes et 136 pattes. Combien a-t-il de poulets et de lapins ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
101
Casse-tête

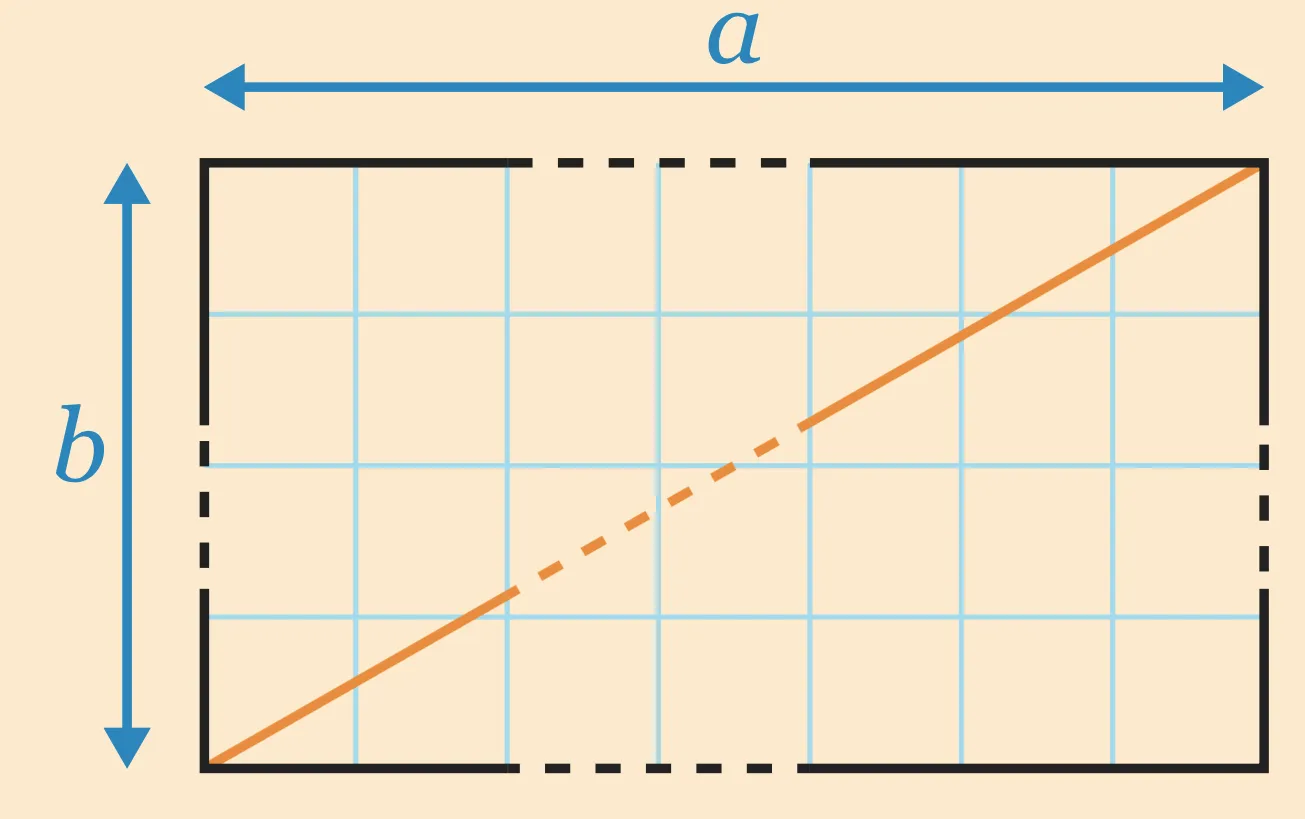
Dans un quadrillage, on dessine un rectangle de longueur a et de largeur b (donc a>b).
1. Combien de carreaux sont coupés par la diagonale du rectangle ?
2. Proposer un algorithme qui compte le nombre de carreaux coupés par la diagonale du rectangle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille