Sommaire

Mes pages

Ouverture

p. 1-11

🔴 Mise à jour 2026 🔴

Ch. A

Statistiques continues

Ch. B

Statistiques bivariées

Ch. C

Probabilités conditionnelles

Ch. D

Valeur absolue

Nombres et calculs

Fonctions

Ch. 1

Généralités sur les fonctions

Ch. 2

Variations de fonctions

Ch. 3

Fonctions affines

Ch. 4

Fonctions de référence

Géométrie

Ch. 5

Repérage et configuration dans le plan

Ch. 6

Notion de vecteur

Ch. 7

Colinéarité de vecteurs

Testez le chapitre 100 % débloqué

Ch. 8

Équations de droites

Statistiques et probabilités

Ch. 9

Informations chiffrées

Ch. 10

Statistiques descriptives

Ch. 11

Probabilités et échantillonnage

Annexes

Exercices transversaux

Cahier d'algorithmique et de programmation

Rappels de collège

Jeux de société

Nos dossiers d'actualité

Dossier d'actualité

Page précédente

Chapitre 8

Entraînement 1

Vecteurs directeurs et équations cartésiennes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercices FLASH

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Associer à chaque équation la droite correspondante.

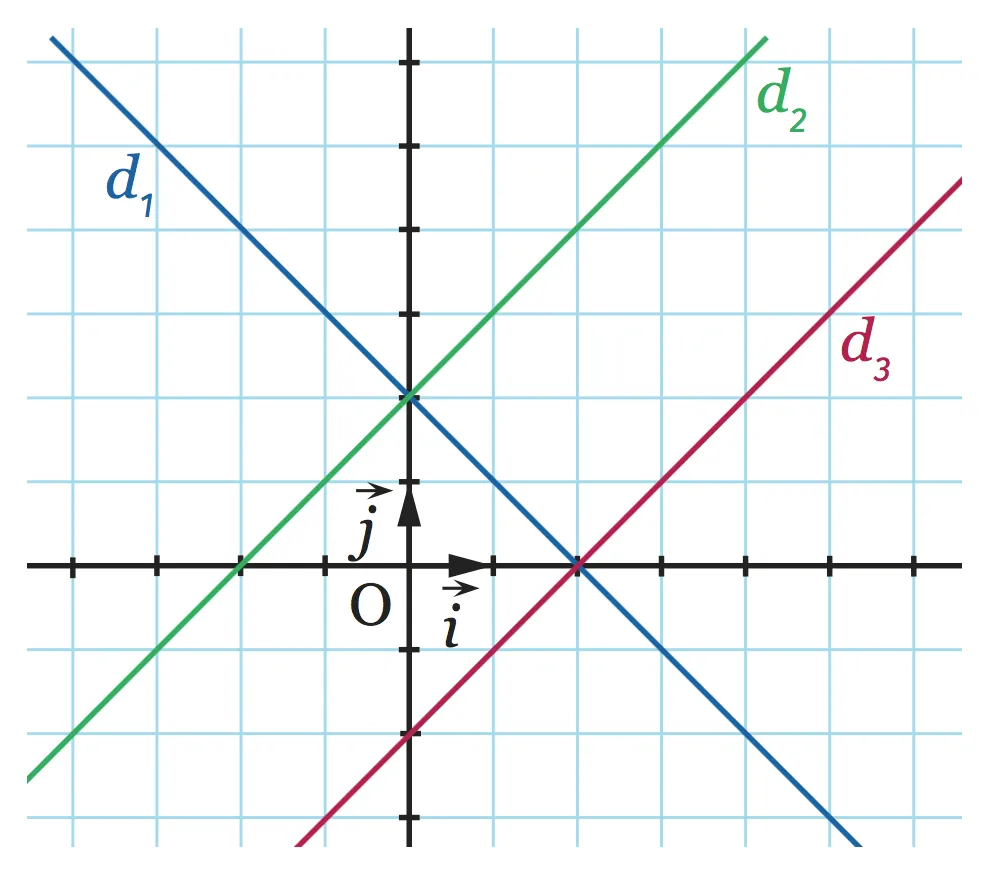
Graphique : trois droites (d1, d2, d3) se croisent sur un plan cartésien. Illustration d'équations linéaires.

y = x + 2

y = x - 2

y = - x + 2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Déterminer l'équation réduite de chacune des droites ci-dessous, sous la forme

y = m x + p

ou sous la forme

x = c

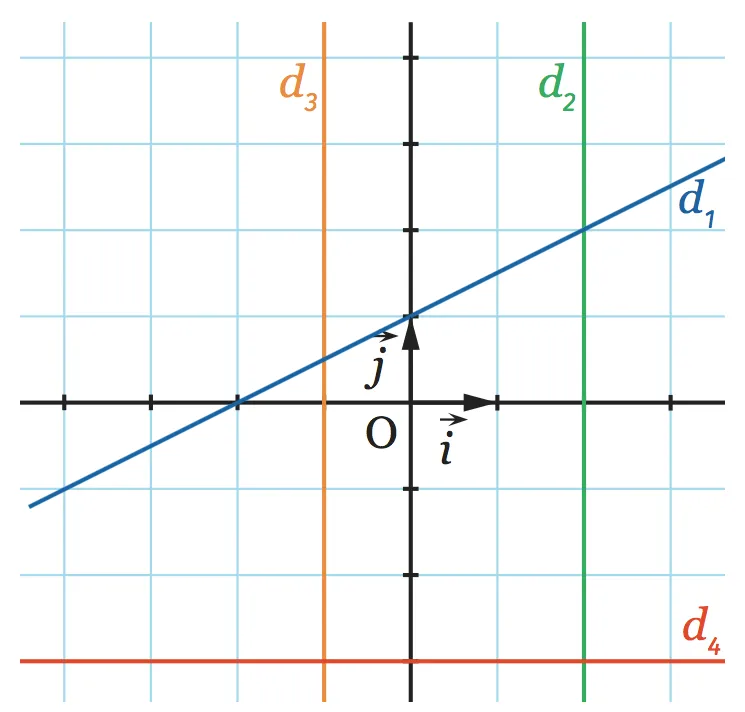
Graphique : droite (d1) et quatre autres (d2, d3, d4) sur plan cartésien.

d_{1}

d_{2}

d_{3}

d_{4}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
Calculer mentalement le coefficient directeur de la droite

(AB)

dans les cas suivants :

1.

A (0; 0)

B (4; 4)

A (- 1; 1)

B (0; 5)

A (4; - 1)

B (3; 1)

A (0; - 2)

B (4; 0)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
Dans chaque cas, déterminer, sans la tracer, si la droite

(AB)

est parallèle à l'un des axes ou non. Si oui, lequel ?

1.

A (3; 3)

B (3; 1)

A (1; - 1)

B (2; - 1)

A (0, 5; 0, 25)

B (0, 25; 0, 5)

A (0, 25; 2)

B (\frac{1}{4}; \frac{4}{8})

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
Tracer dans un repère les droites suivantes :

1.

d_{1} : y = 2 x + 1

d_{2} : y = 0, 5 x

d_{3} : y = 3 x - 2

d_{4} : y = \frac{1}{4} x - 1

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

35
On considère dans un repère orthonormé les points

A (1; 1)

B (2; - 3)

1. Déterminer une équation cartésienne de la droite

d

passant par

B

et de vecteur directeur

u (- 1 2) .

2. Le point

A

appartient-il à la droite

d

? Justifier.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercices d'entraînement

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour l'ensemble des exercices, lorsque rien n'est précisé, on se placera dans un repère orthonormé du plan $(O; i, j) .$

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Différenciation

Parcours 1 : exercices

;

Parcours 2 : exercices

;

Parcours 3 : exercices

;

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
[Calculer.]
Dans chacun des cas suivants, indiquer si le vecteur

u

est un vecteur directeur de la droite

(AB)

.
1.

A (1; 0)

B (0; 1)

;

u (11)

A (2; 3)

B (- 3; 4)

;

u (5 - 1)

A (- 1; 4)

B (- 2; 6)

;

u (21)

A (4; - 2)

B (1; 1)

;

u (1 - 1)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
[Chercher.]

On se place dans un repère orthonormé du plan

(O; i, j) .

Vecteurs directeurs et équations cartésiennes

Déterminer les coordonnées d'un vecteur directeur pour chacune des droites représentées dans le repère.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
[Représenter.]
Représenter dans un repère la droite passant par le point

A

et de vecteur directeur

u

.

1. Droite

d_{1} : A (1; 1)

u (- 1; 3)

2. Droite

d_{2} : A (- 2; 1)

u (5; 1)

3. Droite

d_{3} : A (0; 3)

u (3; 0)

4. Droite

d_{4} : A (- 4; 0)

u (0; 5)

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

39
[Représenter.]

Représenter dans le repère chacune des droites suivantes dont on donne une équation cartésienne.

1.

d_{1} : x + y + 1 = 0

d_{2} : 2 x - y - 2 = 0

d_{3} : - x + 2 y + 3 = 0

d_{4} : 3 x - 2 y + 3 = 0

d_{5} : 2 x + 3 y - 4 = 0

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

40
[Chercher.]
Par lecture graphique, déterminer une équation cartésienne pour chacune des droites représentées dans le repère.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

41
[Communiquer.]
Dans chaque cas, démontrer que l'équation de droite écrite est une équation de la droite

(AB) .

y = - 23 x + 18

A (2; - 28)

B (- 1; 41)

y = - x 2 + 4

A (2; 2)

B (- 2; 6)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
[Calculer.]
Parmi les équations suivantes, quelles sont celles qui sont des équations de droites ?

3 y = 2 - 4 x

- 3 (1 + x) + y = 0

(1 + y) (1 - x) = 5

x y = 5

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

43
[Calculer.]
Parmi les équations suivantes, quelles sont celles qui sont des équations de droites ?

\frac{1}{x} - y + 3 = 0

(- 3 x + 1) (2 + y) = 4

\frac{x + y}{3} - \frac{1}{4} = 5

x + y - 1 = 6

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
[Raisonner.]
Dans chaque cas, déterminer en justifiant si le point

A

appartient à la droite

d

.

1.

d : x + 4 y - 20 = 0

A (- 4; 9)

d : 2 x - 3 y - 1 = 0

A (12; 5)

d : \frac{- 2}{3} x + 2 y - \frac{2}{3} = 0

A (1; \frac{2}{3})

d : \frac{- 4}{5} x - \frac{1}{2} y - 1 = 0

A (\frac{1}{2}; 3)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
[Calculer.]
Calculer l'ordonnée du point

A

pour qu'il appartienne à la droite

d

:

1.

A

a pour abscisse

- 5

d

a pour équation

3 x - y - 2 = 0.

A

a pour abscisse

\frac{1}{2}

d

a pour équation

7 x + y - 1 = 0.

A

a pour abscisse

\frac{4}{3}

d

a pour équation

\frac{1}{2} x + \frac{1}{3} y + \frac{1}{4} = 0.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

46
[Calculer.]
Calculer l'abscisse du point

A

pour qu'il appartienne à la droite

d

:

1.

A

a pour ordonnée

\frac{- 3}{2}

d

a pour équation

3 x - y - 2 = 0.

A

a pour ordonnée

\frac{1}{2}

d

a pour équation

- 7 x - y + 1 = 0.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

47
[Calculer.]

Calculer l'abcisse du point

A

pour qu'il appartienne à la droite

d

:
1.

A

a pour ordonnée

4

d

a pour équation

\frac{1}{3} x + \frac{2}{5} y - 1 = 0.

A

a pour ordonnée

2

d

a pour équation

\frac{3}{2} x + 5 y - 2 = 0.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

48
[Chercher.]

Soit

d

une droite passant par le point

A

et de vecteur directeur

u

.
Dans chacun des cas suivants, déterminer une équation cartésienne de la droite

d

:

1.

A (0; 0)

u (11)

A (1; 2)

u (1 - 2)

A (- 3; - 1)

u (- 2 1)

A (\frac{1}{2}; \frac{1}{2})

u (- 3 - 1)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

49
[Calculer.]

Dans chacun des cas suivants, déterminer une équation cartésienne de la droite

(AB)

.

1.

A (0; 1)

B (1; 0)

A (2; 1)

B (- 1; 6)

A (\frac{2}{3}; - \frac{1}{2})

B (\frac{- 1}{3}; - \frac{3}{2})

A (- 2; - 23)

B (32; 3)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

50
[Calculer.]

Dans chacun des cas suivants, déterminer une équation cartésienne de la droite

d

parallèle à la droite

(AB)

et passant par le point

C

.

1.

A (1; 0)

B (0; 1)

C (3; - 2)

A (1; - 3)

B (2; 1)

C (1; 1)

A (- 2; - 2)

B (1; - 5)

C (- 6; 2)

A (- 5; 1)

B (- 1; - 1)

C (- 2; - 2)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

51
Algo
[Calculer.]

d

est une droite de vecteur directeur

u

de coordonnées

(α β)

et passant par un point

A (x; y)

où

α

β

x

y

sont des réels saisis par l'utilisateur.

1. Écrire un algorithme en langage naturel qui donne les coefficients

a

b

c

d'une équation cartésienne de la droite

d .

2. Le traduire en langage Python.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
Vrai / Faux
[Raisonner.]
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.

1. « L'ensemble des points du plan de coordonnées

(x; y)

tels que

2 x (y + 1) - (x + 1) (2 y + 1) = 2

est une droite. »

2. « Le vecteur

v (3 - 2)

est un vecteur directeur de la droite

d

d'équation cartésienne

6 x + 9 y - 1 = 0.

»

3. « Les droites d'équation cartésienne

4 x + 8 y - 3 = 0

- 5 x + 10 y + 7 = 0

sont parallèles. »

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
[Représenter.]
Dans un jeu de cartes sur ordinateur, on reçoit 1 000 gemmes à la première utilisation et chaque mission quotidienne rapporte 300 gemmes.

Photographie de cartes Magic : l'Assemblée, des terrains de base (Île, Plaine, Marais, Forêt) disposés sur une table avec des dés.

1. Compléter le tableau suivant qui donne le gain quotidien :

Jours de jeu	0	1	2	3	10	15	20
Gemmes en possession

2. Dans un repère orthogonal, représenter le tableau ci-dessus par un nuage de points (on prendra 1 cm pour 2 jours en abscisses et 1 cm pour 500 gemmes en ordonnées).

3. Expliquer pourquoi les points sont alignés et déterminer une équation de la droite passant par ces points.

4. Combien de jours minimum faut-il jouer pour se payer l'inscription à un tournoi à 4 800 gemmes ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
[Représenter.]

On construit une suite de carrés tronqués à chaque sommet comme dans la figure ci-dessous. On note

n

la longueur du côté du carré exprimée en cm (

n

supérieur ou égal à 2).

1. Quel est le périmètre du premier polygone (le plus petit) ? Et du deuxième ?

2. Exprimer le périmètre

P_{n}

du n-ième polygone en fonction de

n

3. Représenter graphiquement les points

(n; y)

où

y = P_{n}

dans un repère orthogonal donc on choisira bien l'unité.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

4. Que constate-t-on ?

5. Établir les dimensions du polygone dont le périmètre dépasse 1 m. Vérifier par le calcul.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55

Algo
[Représenter.]
Une ville

A

compte 6 000 habitants au 1^er janvier 2018 et sa démographie montre une augmentation de 150 habitants en moyenne par an.
Une ville

B

qui compte 8 000 habitants perd 80 habitants par an.
On souhaite déterminer le nombre d'années au bout duquel la population de la ville

A

aura dépassé la population de la ville

B

.

1. Représenter graphiquement l'évolution des deux populations et conjecturer graphiquement la réponse au problème posé.

2. a. Recopier et compléter l'algorithme suivant :

6000 \leftarrow A 8000 \leftarrow B 2018 \leftarrow N Tant que \dots A \leftarrow \dots B \leftarrow \dots N \leftarrow N + 1 Fin Tant que

b. Quelles seront les valeurs prises par

A

B

C

lorsque l'algorithme s'arrêtera ?

Page suivante

Statistiques continues

Statistiques bivariées

Probabilités conditionnelles

Valeur absolue

Nombres et calculs

Généralités sur les fonctions

Variations de fonctions

Fonctions affines

Fonctions de référence

Repérage et configuration dans le plan

Notion de vecteur

Colinéarité de vecteurs

Équations de droites

Informations chiffrées

Statistiques descriptives

Probabilités et échantillonnage

Exercices transversaux

Cahier d'algorithmique et de programmation

Rappels de collège

Jeux de société

Vecteurs directeurs et équations cartésiennes

Exercices FLASH

GeoGebra

Exercices d'entraînement

Pour l'ensemble des exercices, lorsque rien n'est précisé, on se placera dans un repère orthonormé du plan (O;i,j​).

Différenciation

GeoGebra

GeoGebra

GeoGebra

Pour l'ensemble des exercices, lorsque rien n'est précisé, on se placera dans un repère orthonormé du plan $(O; i, j) .$