Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 2
TP / TICE 2
Dimensions d'une boîte de conserve
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Par souci d'économie, les industriels choisissent souvent les dimensions
d'une boîte de conserve de manière à utiliser le moins de métal, pour un
volume donné. Dans ce TP, la boîte de conserve est assimilée à un cylindre
de révolution de rayon r et de hauteur h , exprimés en centimètres.
L'épaisseur du métal étant la même sur toute la surface, le volume de métal
nécessaire est proportionnel à l'aire de la boîte.
Question préliminaire : Après avoir dessiné la figure en perspective cavalière
et le patron d'un cylindre de révolution, rappeler les formules donnant le
volume V et la surface totale extérieure S de la boîte de conserve.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
À l'aide d'une des deux méthodes, déterminer les dimensions
optimales d'une boîte de conserve de volume V = 900 cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Montrer, avec la contrainte de volume, que l'aire
totale est obtenue en fonction du rayon x grâce à
la fonction S, définie sur ] 0\: ;+\infty[ par :
\mathrm{S}(x)=2 \pi x\left(x+\dfrac{900}{\pi x^{2}}\right).
2. a. Représenter cette fonction avec GeoGebra.
b. Modifier la zone d'affichage du graphique pour cadrer la fenêtre sur la partie qui nous intéresse.
2. a. Représenter cette fonction avec GeoGebra.
b. Modifier la zone d'affichage du graphique pour cadrer la fenêtre sur la partie qui nous intéresse.
GeoGebra
3. Émettre une conjecture sur les variations de S.
Sont-elles surprenantes ? Comment peut-on les expliquer ?
4. Déterminer le rayon optimal de la boîte ainsi que la hauteur correspondante.
5. Les dimensions d'une boîte 4/4 sont r = 4{,}95 cm et h = 11{,}8 cm. La surface est-elle optimisée pour cette boîte ?
4. Déterminer le rayon optimal de la boîte ainsi que la hauteur correspondante.
5. Les dimensions d'une boîte 4/4 sont r = 4{,}95 cm et h = 11{,}8 cm. La surface est-elle optimisée pour cette boîte ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Reproduire la feuille de calcul ci-dessous puis
répondre aux questions qui suivent.
Le zoom est accessible dans la version Premium.
GeoGebra
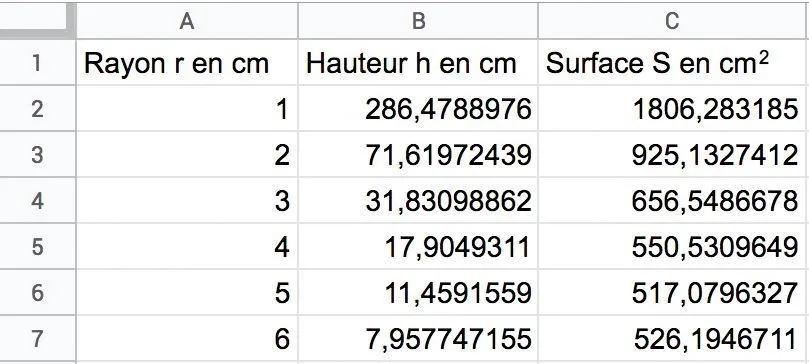
2. Quelle formule doit-on indiquer dans la cellule
B2 pour automatiser le calcul de la hauteur lorsque
l'on connaît le rayon et le volume de la boîte ?
3. Expliquer la formule appliquée dans la cellule C2.
4. À la lecture de la capture d'écran, quel encadrement du rayon optimal peut-on donner ?
5. En affinant le choix des valeurs du rayon, déterminer une valeur approchée au centième près du rayon optimal de la boîte ainsi que la hauteur correspondante.
6. Les dimensions d'une boîte 4/4 sont r = 4{,}95 cm et h = 11{,}8 cm. La surface est-elle optimisée pour cette boîte ?
3. Expliquer la formule appliquée dans la cellule C2.
4. À la lecture de la capture d'écran, quel encadrement du rayon optimal peut-on donner ?
5. En affinant le choix des valeurs du rayon, déterminer une valeur approchée au centième près du rayon optimal de la boîte ainsi que la hauteur correspondante.
6. Les dimensions d'une boîte 4/4 sont r = 4{,}95 cm et h = 11{,}8 cm. La surface est-elle optimisée pour cette boîte ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les canettes de soda de 33 cL ont une forme
proche d'un cylindre de révolution.
Les canettes classiques ont un diamètre de 66 mm
et une hauteur de 115 mm. Les canettes sleek ont
un diamètre de 58 mm et une hauteur de 145 mm.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
1. Vérifier que chaque type de canette peut bien
contenir 33 cL de liquide.
2. Quelle est la surface de métal nécessaire pour construire une canette de chacun de ces types ?
3. La différence entre les deux surfaces est-elle négligeable ?
2. Quelle est la surface de métal nécessaire pour construire une canette de chacun de ces types ?
3. La différence entre les deux surfaces est-elle négligeable ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah