Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 3
Entraînement 2
Étude d'une fonction affine
14 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Raisonner.]
Soit g la fonction définie sur \mathbb{R} par g(x)=\dfrac{13}{6} x-\dfrac{2}{9}.
1. Comparer g\left(-\dfrac{2}{3}\right) et g\left(-\dfrac{7}{4}\right) en utilisant les variations de g.
2.Comparer g\left(-\dfrac{2}{3}\right) et g\left(-\dfrac{7}{4}\right) à l'aide d'une chaîne logique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Chercher.] Classer les fonctions suivantes selon leur variation (croissante, décroissante, constante) sur \mathbb{R}.
g(x)=4 x-3
h(x)=(-6 x+1)-2(4 x-3)
i(x)=2(-6 x+1)+3(4 x-3)
h(x)=(-6 x+1)-2(4 x-3)
i(x)=2(-6 x+1)+3(4 x-3)
j(x)=-3(-6 x+1)-(4 x-3)
k(x)=(-6 x+1)^{2}-9 x(4 x-3)
k(x)=(-6 x+1)^{2}-9 x(4 x-3)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Raisonner.]
Soit f une fonction affine définie sur \mathbb{R}.
Déterminer les extremums de f sur l'intervalle [1 \:; 10] en supposant que :
1. f est croissante sur \mathbb{R} ;
2. f est décroissante sur \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Chercher.]
Classer les fonctions affines suivantes selon leur signe sur l'intervalle [1\: ; 10].
g_{1}(x)=2 x+4
g_{2}(x)=-2 x-4
g_{3}(x)=2 x-4
g_{2}(x)=-2 x-4
g_{3}(x)=2 x-4
g_{4}(x)=-2 x+4
g_{5}(x)=2 x
g_{6}(x)=-4
g_{5}(x)=2 x
g_{6}(x)=-4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Raisonner.] f est une fonction affine définie sur \mathbb{R} par f(x)=m x+p dont on donne le tableau de signes ci-dessous.
Le zoom est accessible dans la version Premium.
1. Le nombre m peut-il être égal à 0 ? Justifier.
2. Peut-on comparer les nombres p et 2 ?
3. Comparer -\dfrac{p}{m}et -1.
2. Peut-on comparer les nombres p et 2 ?
3. Comparer -\dfrac{p}{m}et -1.
4. Établir le tableau de variations de f sur \mathbb{R}.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Raisonner.]
Soient h et k deux fonctions affines écrites sous la forme mx + p avec m \neq 0.
On donne leur tableau de signes ci-dessous :
Le zoom est accessible dans la version Premium.
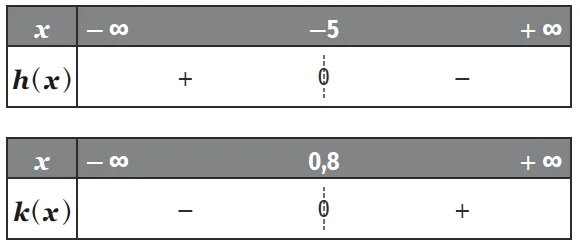
1. Pour chaque fonction, donner la valeur de \dfrac{-p}{m}.
2. Pour chaque fonction, recopier et compléter par le plus petit intervalle possible :
m \in ] \ldots ; \ldots[ et p \in] \ldots ; \ldots[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Chercher.] Soient r et s deux fonctions affines définies sur \mathbb{R} par r(x)=4-\dfrac{3}{7} x et s(x)=x-\dfrac{1}{2}.
1. Dresser le tableau de variations sur \mathbb{R} de chacune de ces fonctions.
2. Déterminer l'expression algébrique de la fonction t définie pour tout réel x par t(x)=r(x)+s(x).
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. Déterminer l'expression algébrique de la fonction t définie pour tout réel x par t(x)=r(x)+s(x).
3. En déduire le tableau de variations de t sur \mathbb{R}.
4. Conjecturer une propriété pour établir les variations de la somme de deux fonctions affines.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. Conjecturer une propriété pour établir les variations de la somme de deux fonctions affines.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Chercher.]
Soient p et q deux fonctions affines définies sur \mathbb{R} par p(x)=10-6 x et q(x)=-8 x+2.
1. Donner le tableau de signes de chacune de ces fonctions sur \mathbb{R}.
2. Déterminer l'expression algébrique de la fonction d définie pour tout réel x par d(x)=p(x)-q(x).
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. Déterminer l'expression algébrique de la fonction d définie pour tout réel x par d(x)=p(x)-q(x).
3. En déduire le tableau de signes de d sur \mathbb{R}.
4. Que peut-on en déduire sur les positions relatives des courbes représentatives de p et de q ?
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. Que peut-on en déduire sur les positions relatives des courbes représentatives de p et de q ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
Algo
[Modeliser.] Un étudiant a emprunté 1 000 € à ses parents. Il prévoit de rembourser 85 € par mois. On note x le nombre de mois écoulés depuis l'emprunt et S(x) la somme restant à rembourser après x mois.
1. Donner une expression de S(x).
2. Étudier le signe et les variations de la fonction S.
3. En déduire au bout de combien de mois l'étudiant aura payé sa dette.
2. Étudier le signe et les variations de la fonction S.
3. En déduire au bout de combien de mois l'étudiant aura payé sa dette.
4. Compléter l'algorithme ci-dessous pour que celui-ci donne le nombre de mois nécessaires pour recouvrir la dette de l'étudiant.
\boxed{
\begin{array} { l } { \text {D } \leftarrow 1000 } \\ { \text {X } \leftarrow 0 } \\
\text{Tant que ... }\\
\quad \text {X } \leftarrow \text { X }+1 \\
\quad \text {D } \leftarrow ... \\
\text {Fin Tant que}
\end{array}
}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Calculer.]
On souhaite résoudre dans \mathbb{R} l'inéquation :
(4 x-3)(2 x-1) \geqslant 0.
1. Déterminer, en fonction de x, le signe de 4x - 3 puis celui de 2x - 1.
2. Rassembler les réponses dans un tableau de signes et en déduire la résolution du problème.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Calculer.]
On souhaite résoudre dans \mathbb{R} l'inéquation \dfrac{3 x-4}{-2 x+1}>0.
1. Déterminer, en fonction de x, le signe de 3x - 4 puis celui de -2x + 1.
2. Rassembler les réponses dans un tableau de signes et en déduire la résolution du problème.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre dans \mathbb{R} les inéquations proposées en faisant attention aux ensembles de définition.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Calculer.]
1. (-2 x+1)(6 x+5)>0
2. (2-3 x)(4 x-1) \leqslant 0
3. \left(\dfrac{1}{2} x+3\right)\left(\dfrac{-2}{3} x-\dfrac{1}{2}\right)\lt0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Calculer.] 1. (5 x-3)(2 x+1)>(2 x+1)(x-4)
2. (3 x+2)(-6 x-1) \geqslant(3 x+2)^{2}
3. (2 x-1)(-5 x+7) \lt 4 x^{2}-4 x+1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
[Calculer.]
1. \dfrac{x+2}{-x+6} \lt 0
2. \dfrac{3 x-4}{2 x+3} \geqslant 0
3. \dfrac{\dfrac{1}{2} x-7}{8 x+\dfrac{1}{3}} \leqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Calculer.]
1. \dfrac{x-4}{x+8}>-1
2. \dfrac{x}{2 x-10} \geqslant 2
3. \dfrac{1-4 x}{x-3} \lt -4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Raisonner.]
1. Montrer que, pour tout x \in \mathbb{R},
(x+5)(x+3)-15=x(x+8)
2. En déduire les solutions de l'inéquation :
(x+5)(x+3)>15
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
[Raisonner.]
1. Montrer que, pour tout x \in \mathbb{R},
(-2 x+1)(x-3)+25=(-2 x+11)(x+2)
2. En déduire les solutions de l'inéquation :
(-2 x+1)(x-3) \geqslant-25
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
[Raisonner.]
1. Montrer que, pour tout x \in \mathbb{R},
7+(-2 x+7)(x-6)=(-x+7)(2 x-5).
2. En déduire les solutions de l'inéquation :
(-2 x+7)(x-6) \lt -7.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Raisonner.] Soit p un nombre réel. On pose m_p le réel défini par m_{p}=-7 p+3.
On considère la famille de fonctions affines notées f_p définies sur \mathbb{R} par f_{p}(x)=m_{p} \times x+p.
1. a. Montrer que m_{1}=-4.
b. En déduire l'expression de la fonction f_{1}.
2. Déterminer l'expression de la fonction f_{-2}.
3. En fonction des valeurs de p, discuter :
a. des variations de la fonction f_{p} ;
b. du signe de l'éventuelle valeur annulant f_{p}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
Démo
[Raisonner.]
1. Montrer qu'une fonction linéaire est une fonction impaire.
2. Montrer qu'une fonction constante est une fonction paire.
3. Démontrer les réciproques des deux propositions précédentes dans le cas de fonctions affines.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Raisonner.] Soient f et g deux fonctions définies pour tout x \in \mathbb{R} par f(x)=4 x-6 \text { et } g(x)=-5 x+3.
1. Étudier les variations de f et g sur \mathbb{R}.
2. Soit a un réel tel que a \in[-1\:; 2].
a. Donner un encadrement de f(a) puis de g(f(a)).
b. Donner un encadrement de g(a) puis de f(g(a)).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
[Raisonner.]
Soit f une fonction affine définie sur \mathbb{R} telle que :
5 \leqslant x \leqslant 9 \Leftrightarrow-8 \leqslant f(x) \leqslant 3.
Quelle doit être alors l'expression de f pour que la fonction f :
1. soit croissante ?
2. soit décroissante ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
Démo
[Raisonner.]
On considère une fonction affine f définie sur \mathbb{R} par f(x)=m x+p où m et p sont deux nombres réels tels que m \neq 0.
1.
Déterminer la solution de l'équation f(x)=0 en fonction de m et p.
2. On suppose que m>0.
a. Quel est le sens de variation de f sur \mathbb{R} ?
b. x_1 et x_2 sont deux nombres réels tels que
x_{1} \lt -\dfrac{m}{p} \lt x_{2}.
Déterminer le signe de f (x_1) et f( x_2).
c. Dresser alors le tableau de signes de f sur \mathbb{R} lorsque m > 0.
2. On suppose que m>0.
a. Quel est le sens de variation de f sur \mathbb{R} ?
b. x_1 et x_2 sont deux nombres réels tels que
x_{1} \lt -\dfrac{m}{p} \lt x_{2}.
Déterminer le signe de f (x_1) et f( x_2).
c. Dresser alors le tableau de signes de f sur \mathbb{R} lorsque m > 0.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. On suppose que m \lt 0. En utilisant le même raisonnement que dans la question 2. , dresser le tableau de signes de f sur \mathbb{R} lorsque m \lt 0.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah