Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 3
Synthèse
Exercices de Synthèse
8 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
Démo
[Raisonner.]
1. a. Démontrer la proposition suivante :
« Si f est une fonction affine alors pour tous réels u et v, f\left(\dfrac{u+v}{2}\right)=\dfrac{f(u)+f(v)}{2}. »
b. Reformuler cette propriété en terme de moyenne.
« Si f est une fonction affine alors pour tous réels u et v, f\left(\dfrac{u+v}{2}\right)=\dfrac{f(u)+f(v)}{2}. »
b. Reformuler cette propriété en terme de moyenne.
2. a. Démontrer que la somme de deux fonctions affines est une fonction affine.
b. Reformuler cette proposition sous la forme « Si ... alors ... » (prendre exemple sur la question 1. a.).
b. Reformuler cette proposition sous la forme « Si ... alors ... » (prendre exemple sur la question 1. a.).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
[Chercher.] Pour les Jeux olympiques de 2024 à Paris, on envisage de construire une salle multisport suivant les contraintes indiquées ci-dessous (avec x compris entre 10 et 50 mètres).
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
1. Déterminer l'aire \mathrm{T}_{\mathrm{S}} du terrain de sport en fonction de x.
2. On note \mathrm{T}_{\mathrm{B}}, l'aire au sol de la tribune basse.
Démontrer que, pour tout x \in[10 \:; 50],
\mathrm{T}_{\mathrm{B}}(x)=(x+20)(x+30)-\mathrm{T}_{\mathrm{S}}(x) puis simplifier l'expression de \mathrm{T}_{\mathrm{B}}.
3. On note \mathrm{T}_{\mathrm{H}}, l'aire au sol de la tribune haute.
Démontrer que, pour tout x \in[10 \:; 50],
\mathrm{T}_{\mathrm{H}}(x)=(x+60)(x+70)-(x+20)(x+30) puis simplifier l'expression de \mathrm{T}_{\mathrm{H}}.
4. Le coût de construction du mètre carré en tribune basse est trois fois plus élevé qu'en tribune haute.
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions \mathrm{T}_{\mathrm{H}} et 3 \times \mathrm{T}_{\mathrm{B}}.
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse coûtera moins cher que la tribune haute.
(On pourra noter c le coût de construction au mètre carré de la tribune haute.)
2. On note \mathrm{T}_{\mathrm{B}}, l'aire au sol de la tribune basse.
Démontrer que, pour tout x \in[10 \:; 50],
\mathrm{T}_{\mathrm{B}}(x)=(x+20)(x+30)-\mathrm{T}_{\mathrm{S}}(x) puis simplifier l'expression de \mathrm{T}_{\mathrm{B}}.
3. On note \mathrm{T}_{\mathrm{H}}, l'aire au sol de la tribune haute.
Démontrer que, pour tout x \in[10 \:; 50],
\mathrm{T}_{\mathrm{H}}(x)=(x+60)(x+70)-(x+20)(x+30) puis simplifier l'expression de \mathrm{T}_{\mathrm{H}}.
4. Le coût de construction du mètre carré en tribune basse est trois fois plus élevé qu'en tribune haute.
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions \mathrm{T}_{\mathrm{H}} et 3 \times \mathrm{T}_{\mathrm{B}}.
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse coûtera moins cher que la tribune haute.
(On pourra noter c le coût de construction au mètre carré de la tribune haute.)
5. Pendant les Jeux olympiques, le prix des places au mètre carré en tribune haute est quatre fois moins important qu'en tribune basse.
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions \mathrm{T}_{\mathrm{B}} et \dfrac{1}{4} \times \mathrm{T}_{\mathrm{H}}.
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse engendrera plus de recettes que la tribune haute.
(On pourra noter p le prix au mètre carré des places de la tribune basse.)
a. Représenter, à l'aide de la calculatrice ou de GeoGebra, les fonctions \mathrm{T}_{\mathrm{B}} et \dfrac{1}{4} \times \mathrm{T}_{\mathrm{H}}.
b. Déterminer graphiquement puis algébriquement les valeurs de x pour lesquelles la tribune basse engendrera plus de recettes que la tribune haute.
(On pourra noter p le prix au mètre carré des places de la tribune basse.)
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
[Modéliser.] Un nouveau journal communal d'une ville de 6 000 habitants a imprimé 1 000 exemplaires de son premier numéro et les a tous vendus au prix de 2 € chacun.
Une étude de marché montre que si le prix du journal baissait d'un certain pourcentage \dfrac{x}{100}, les ventes augmenteraient significativement.
Le but est d'étudier le chiffre d'affaire potentiel pour les prochains numéros en fonction de x \in[0 \:; 100].
Le comptable a déterminé que le chiffre d'affaire \mathrm{C} du journal est défini pour tout x \in[0 \:; 100] par :
\mathrm{C}(x)=2\,000+80 x-x^{2}.
1. a. Démontrer que pour tout x \in[0 \:; 100],
\text{C}(x)=(-x+20)(x-60)+3\,200.
b. Résoudre l'in équation \mathrm{C}(x) \geqslant 3\,200, puis interpréter le résultat.
\text{C}(x)=(-x+20)(x-60)+3\,200.
b. Résoudre l'in équation \mathrm{C}(x) \geqslant 3\,200, puis interpréter le résultat.
2. a. Démontrer que pour tout x \in[0 \:; 100],
\mathrm{C}(x)\lt1\,100 \Leftrightarrow(-x-10)(x-90)\lt0.
b. En déduire les solutions de l'inéquation {\mathrm{C}(x)\lt1\,100} puis interpréter le résultat.
\mathrm{C}(x)\lt1\,100 \Leftrightarrow(-x-10)(x-90)\lt0.
b. En déduire les solutions de l'inéquation {\mathrm{C}(x)\lt1\,100} puis interpréter le résultat.
3. Résoudre les inéquations \mathrm{C}(x)>2\,000 et \text{C}(x) \leqslant 3\,600 puis interpréter les résultats.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
Python
[Modeliser.] Réda veut faire état à Arthur de ses talents de magicien. Pour cela, il lui demande de choisir un nombre entier entre 0 et 50 et de le garder pour lui tout en suivant ces étapes.
• Ajouter 5 au nombre choisi.
• Multiplier par 10 la somme précédente.
• Soustraire le nombre initialement choisi au produit précédent.
• Soustraire 10 au résultat précédent.
1. a. Arthur a choisi 10. Quel résultat va-t-il annoncer ?
b. Quelle fonction affine permet de déterminer le résultat final à partir d'une valeur x initiale ?
c. Écrire un programme avec Python permettant de trouver le résultat final lorsque le nombre de départ est connu.
b. Quelle fonction affine permet de déterminer le résultat final à partir d'une valeur x initiale ?
c. Écrire un programme avec Python permettant de trouver le résultat final lorsque le nombre de départ est connu.
2. Arthur indique le résultat final : 238.
a. Quel nombre a-t-il choisi ?
b. Écrire un programme permettant à Réda de déterminer le nombre initial à partir du résultat final.
a. Quel nombre a-t-il choisi ?
b. Écrire un programme permettant à Réda de déterminer le nombre initial à partir du résultat final.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
89
[Communiquer.]
Deux amis veulent construire un dispositif pour mesurer le temps avec de l'eau. Le temps t est donné en minutes. Au début de l'expérience, on pose t = 0.
Younes élabore un récipient d'eau d'une hauteur de 1 m percé à la base (clepsydre). Il est rempli au début et Younes observe qu'il faut 15 min pour qu'il se vide complètement. La variation de la hauteur de l'eau est proportionnelle au temps.
Amina conçoit un récipient d'eau non percé de la forme d'un pavé droit de 0,8 m de hauteur et de base carrée de 60 cm de côté. Le récipient est vide au début et est ensuite rempli en continu par une source d'eau à débit constant de 12 L par minute.
On note h_{\mathrm{Y}} et h_{\mathrm{A}} les fonctions qui, au temps t, font correspondre la hauteur de l'eau des récipients respectifs de Younes et Amina.
1. Déterminer h_{\mathrm{Y}}(0) et h_{\mathrm{Y}}(15), puis en déduire la forme algébrique de h_{\mathrm{Y}}.
2. Amina affirme que son récipient sera rempli avant que celui de Younes soit vide. A-t-elle raison ?
3. Amina règle le débit pour que son récipient soit rempli en 15 min.
a. Quel est le nouveau débit ?
2. Amina affirme que son récipient sera rempli avant que celui de Younes soit vide. A-t-elle raison ?
3. Amina règle le débit pour que son récipient soit rempli en 15 min.
a. Quel est le nouveau débit ?
b. Déterminer la forme algébrique de la fonction h_{\mathrm{A}}.
4. Calculer le temps exact nécessaire pour qu'il y ait une hauteur d'eau plus grande dans le récipient d'Amina que dans celui de Younes.
4. Calculer le temps exact nécessaire pour qu'il y ait une hauteur d'eau plus grande dans le récipient d'Amina que dans celui de Younes.
Histoire des maths
Le zoom est accessible dans la version Premium.
Contrairement à ce que l'on pourrait penser, la forme du récipient de Younes ne doit pas être cylindrique pour que l'écoulement de l'eau soit proportionnel au temps.
C'est un problème relatif à la mécanique des fluides qui a été étudié par le mathématicien suisse Daniel Bernoulli (1700-1782).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
90
En médecine
[Représenter.]
Le zoom est accessible dans la version Premium.
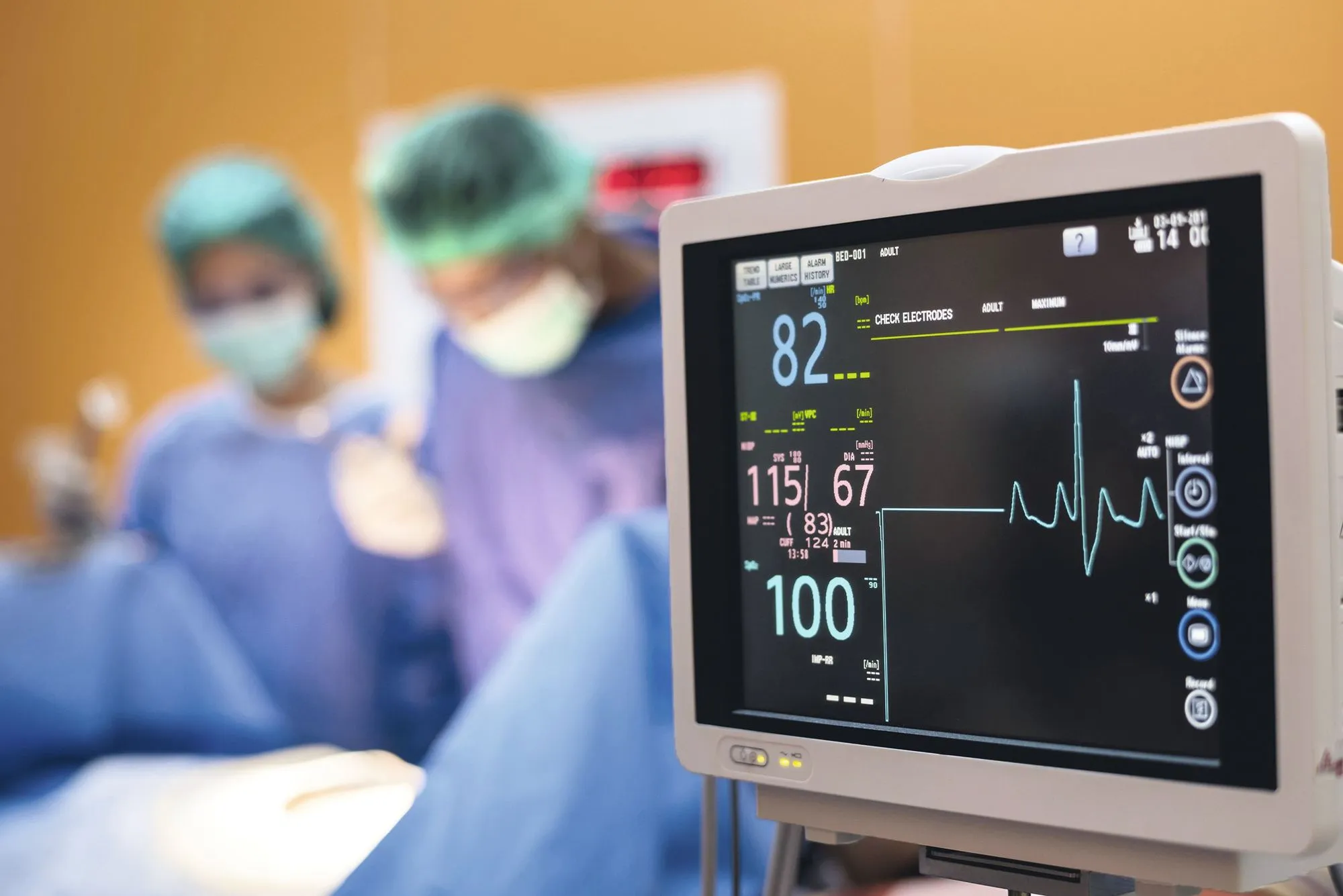
Le complexe \text{QRS} est une partie d'un électrocardiogramme (ECG) correspondant à la dépolarisation des ventricules du cœur. Il est composé de trois ondes : l'onde \text{Q} est la première onde négative, l'onde \text{R} est la première onde positive puis l'onde \text{S} est la deuxième onde négative.
L'étude du complexe \text{QRS} peut révéler certaines pathologies. Par exemple, la normalité est que :
\dfrac{|\text { hauteur onde } \mathrm{Q} |}{|\text { hauteur onde } \mathrm{R} |} \leqslant 0{,}25.
Le zoom est accessible dans la version Premium.
1. Vérifier que c'est le cas chez le patient dont l'ECG est ci-dessus.
2. Un professeur en cardiologie essaye de trouver un autre critère pathogène en relation avec la durée de l'onde \text{Q} (longueur du segment [\text{AB}] sur le graphique) et de l'onde \text{R} (longueur du segment [\text{BC}]). Sur le complexe \text{QRS} étudié :
a. calculer la durée de l'onde \text{Q} ;
2. Un professeur en cardiologie essaye de trouver un autre critère pathogène en relation avec la durée de l'onde \text{Q} (longueur du segment [\text{AB}] sur le graphique) et de l'onde \text{R} (longueur du segment [\text{BC}]). Sur le complexe \text{QRS} étudié :
a. calculer la durée de l'onde \text{Q} ;
b. calculer la durée de l'onde \text{R}.
3. Sur des patients présentant une certaine pathologie, il remarque que {\dfrac{\text { durée onde } \mathrm{Q}}{\text { durée onde } \mathrm{R}}>0{,}25}. Est-ce le cas pour l'ECG de ce patient ? Que peut-on en conclure ?
3. Sur des patients présentant une certaine pathologie, il remarque que {\dfrac{\text { durée onde } \mathrm{Q}}{\text { durée onde } \mathrm{R}}>0{,}25}. Est-ce le cas pour l'ECG de ce patient ? Que peut-on en conclure ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
91
[Modéliser.] David et Antoine achètent un terrain qui doit être partagé en deux perpendiculairement à la route principale. On désigne par x la distance entre le chemin d'accès et la ligne de partage comme ci-dessous.
Le zoom est accessible dans la version Premium.
Le côté d'un carreau mesure 5 mètres.
Partie 1
1. Déterminer l'ensemble de définition de x et l'aire totale du terrain sans prendre en compte la maison.2. Soit \mathrm{A}(x) l'aire du terrain de gauche longeant le chemin d'accès sans prendre en compte la maison.
a. Déterminer \mathrm{A}(x) pour x \in[0 \:; 15].
b. Déterminer \mathrm{A}(x) pour x \in ] 15 \:; 50 ].
c. Représenter la fonction \mathrm{A} dans GeoGebra.
GeoGebra
3. Déterminer graphiquement puis algébriquement la valeur de x pour laquelle le partage est équitable (David et Antoine ont un terrain de même surface).
Partie 2
1. Déterminer le périmètre total du terrain en jaune.2. Soit \mathrm{P}(x), le périmètre du terrain de gauche longeant le chemin d'accès.
a. Déterminer \mathrm{P}(x) pour x \in[0 \:; 15].
b. Déterminer \mathrm{P}(x) pour x \in ] 15 \:; 50 ].
c. Représenter la fonction \text{P} dans le même module GeoGebra qui se trouve dans la Partie 1.
3. On désire clôturer uniquement le terrain longeant le chemin d'accès (y compris le long de la maison). Quelle longueur de clôture (en mètre) doit-on acheter pour effectuer ce travail ? Illustrer graphiquement le résultat dans le module GeoGebra.
4. Le prix du mètre de clôture est de 100 € et le prix du terrain est de 200 € par mètre carré. Quelle doit être la valeur de x pour que les prix des deux terrains (clôture comprise) soient égaux ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
92
[Chercher.]
Un triathlon Ironman comporte 3 phases : 3,8 km de natation, 180,2 km de cyclisme et 42 km de course à pieds.
1. Claire réalise cette épreuve en 15,11 h. Quelle est sa vitesse moyenne sur l'ensemble de l' épreuve ?
2. Elle a effectué la partie natation en 1,9 h et la partie cyclisme en 9,01 h. Quelle est sa vitesse moyenne sur chacune des trois phases ?
3. Voici la représentation de la distance parcourue par l'athlète en fonction du temps.
2. Elle a effectué la partie natation en 1,9 h et la partie cyclisme en 9,01 h. Quelle est sa vitesse moyenne sur chacune des trois phases ?
3. Voici la représentation de la distance parcourue par l'athlète en fonction du temps.
Le zoom est accessible dans la version Premium.
a. Donner les coordonnées des points \text{N}, \text{C} et \text{P} mis en évidence dans le graphique à l'aide des informations.
b. Comment retrouver graphiquement les vitesses moyennes de chacune des trois phases du triathlon ?
c. Donner les expressions algébriques correspondant à cette fonction.
b. Comment retrouver graphiquement les vitesses moyennes de chacune des trois phases du triathlon ?
c. Donner les expressions algébriques correspondant à cette fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
93
[Communiquer.]
La pente p (en %) d'une montée (ou d'une descente) est le rapport entre la différence d'altitude \text{H} entre les points d'arrivée et de départ sur la distance parcourue \text{D} à une même altitude relativement à ces points dans la même unité de mesure.
Le zoom est accessible dans la version Premium.
Le graphique ci-après représente le profil du voyage de Frodon dans Le Seigneur des Anneaux. En abscisse, une unité correspond à la distance parcourue \text{D} de 10 km.
En ordonnée, une unité correspond à l'altitude \text{H} de 0,1 km.
En ordonnée, une unité correspond à l'altitude \text{H} de 0,1 km.
Le zoom est accessible dans la version Premium.
2. Calculer les pourcentages qui correspondent au Mont Caradhras, au Mont Methedras, au Mont Destin et aux plateaux l'entourant.
3. Déterminer la forme algébrique des fonctions qui permettent de tracer ce profil. Que remarquez vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
94
[Calculer.]
Au XIXe siècle, un alpiniste décide de défier une chaîne de montagne africaine, les monts de Kong.
Le zoom est accessible dans la version Premium.
Représenter le profil de l'expédition qui prévoit de partir d'une altitude de 300 m, de parcourir un plateau de 20 km, de grimper le Mont Rennel à 4 % qui culmine à 1 500 m d'altitude et de descendre celui-ci à 2,5 % jusqu'à une altitude de 1 000 m.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de Maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
95
Défi
Soit f une fonction affine définie pour tout x \in \mathbb{R} par f(x)=m x+p.
On appelle f^2 la fonction définie pour tout x \in \mathbb{R} par f^2(x)=f(f(x)).
On généralise cette notation pour n \in \mathbb{N} :
pour tout x \in \mathbb{R}, f^{n+1}(x)=f^{n}(f(x)) et f^{0}(x)=x.
1. Vérifier que pour n = 1, n = 2 et n = 3, les fonctions f^n sont affines.
2. Quelle conjecture peut-on faire sur le coefficient directeur et pour l'ordonnée à l'origine de f^n avec n \in \mathbb{N}^{*} ?
3. Déterminer la seule fonction affine f avec m \in \mathbb{N} et p \in \mathbb{N} vérifiant la propriété suivante :
« Il existe n \in \mathbb{N} telle que, pour tout x \in \mathbb{R}, f^{n}(x)=2\,048 x-2\,047. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
96
Défi
Soit f et g deux fonctions affine définies pour tout x \in \mathbb{R} par f(x)=m x+p et g(x)=r x+s.
Déterminer une condition nécessaire et suffisante sur les nombres s et p pour avoir :
pour tout x \in \mathbb{R}, f(g(x))=g(f(x)).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
97
Défi
Soit u \in \mathbb{R}. On pose m_{u}=3 u-1 et p_{u}=5-2 u.
f_u est une famille de fonctions affines définies sur \mathbb{R} par :
f_{u}(x)=m_{u} \times x+p_{u}.
Déterminer le nombre \lambda qui possède la même image par toutes les fonctions f_u. Quelle est cette image ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
98
Énigme
Je suis une fonction affine décroissante. Si on me multiplie par mon coefficient directeur ou par mon ordonnée à l'origine, ma courbe représentative passe par le point de coordonnées (1 \:; 4). Qui suis-je ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah