• Une fonction f définie sur \mathbb{R} est dite affine lorsqu'il existe deux réels m et p tels que, pour tout x \in \mathbb{R}, f(x)=m x+p.
• Les nombres m et p sont respectivement appelés le coefficient directeur et l'ordonnée à l'origine de f.

Pour une fonction affine donnée, il y a unicité des réels m et p.

Déplacer les curseurs m et p pour modifier le coefficient directeur et l'ordonnée à l'origine de la droite.

Si f est une fonction affine telle que :

• m = 0, alors la fonction f est une fonction constante.
• p = 0, alors la fonction f est une fonction linéaire.

Cette propriété caractérise les fonctions affines.

Le nombre \dfrac{f(b)-f(a)}{b-a} est le taux d'accroissement de f entre a et b.

• Implication : on suppose que f est une fonction affine.
  f(b)=m b+p et f(a)=m a+p donc, si a \neq b,
  
  \dfrac{f(b)-f(a)}{b-a}
  
  =\dfrac{(m b+p)-(m a+p)}{b-a}
  
  =\dfrac{m b+p-m a-p}{b-a}
  
  =\dfrac{m b-m a}{b-a}
  
  =\dfrac{m(b-a)}{b-a}=m.
  Le taux d'accroissement est bien constant.


• Réciproque : Soit a un réel.
  On suppose que, pour tout x \neq a, \dfrac{f(x)-f(a)}{x-a} est constant.
  Pour tout x \neq a, \dfrac{f(x)-f(a)}{x-a}=c
  \Leftrightarrow f(x)-f(a)=c(x-a)
  \Leftrightarrow f(x)=c x-c a+f(a).
  Si x = a, alors on a f(a)=c a-c a+f(a) : l'égalité est donc encore vraie.
  Donc f est une fonction affine avec m = c et p = -ca + f(a) .

Pour démontrer une équivalence
(\text{A} \Leftrightarrow \text{B} : proposition sous la forme « si et seulement si »),
il suffit de démontrer l'implication (\text{A} \Rightarrow \text{B}) et la réciproque (\text{B} \Rightarrow \text{A}).

Soit f une fonction définie sur \mathbb{R} par f(x)=m x+p et a et b deux réels distincts.
Alors, m=\dfrac{f(b)-f(a)}{b-a} \text { et } p=f(a)-ma.

f est une fonction affine telle que f(0)=-5 \text { et } f(1)=-2. Alors : p=f(0)=-5 et m=\dfrac{f(1)-f(0)}{1-0}=\dfrac{-2-(-5)}{1}=-2+5=3. f est donc définie sur \mathbb{R} par f(x)=3 x-5.

p = f(0) et, si a = 0 et b = 1 alors m = f(1) - f(0).

1. Une fonction f est affine si on peut déterminer deux réels m et p tels que, pour tout x \in \mathbb{R}, f(x)=m x+p.

2. Une fonction n'est pas affine lorsque le taux d'accroissement n'est pas constant.

Pour tout réel x, f(x)=1 \times x+1 donc f est affine avec m = 1 et p = 1.
Pour la fonction g, on a : g(0)=-1, g(1)=0 et g(2)=3.

\dfrac{g(2)-g(1)}{2-1}=\dfrac{3-0}{1}=3 et \dfrac{g(1)-g(0)}{1-0}=\dfrac{0-(-1)}{1}=1
Le taux d'accroissement n'est pas constant donc g n'est pas affine.

Exercices

21 et 22

p. 105

Dans un repère orthonormé (\text{O} ; \text{I}, \text{J}), la courbe représentative d'une fonction f est une droite non parallèle à l'axe des ordonnées si et seulement si f est une fonction affine.

La courbe représentative d'une fonction f a pour équation y = f(x).

Soit f une fonction affine définie pour tout x \in \mathbb{R} par f(x)=m x+p.
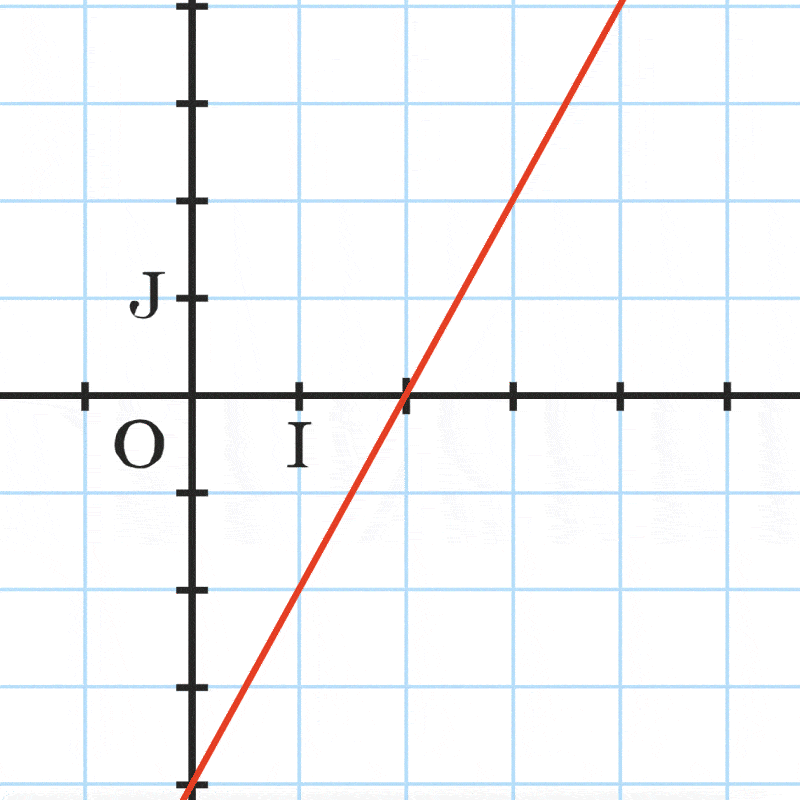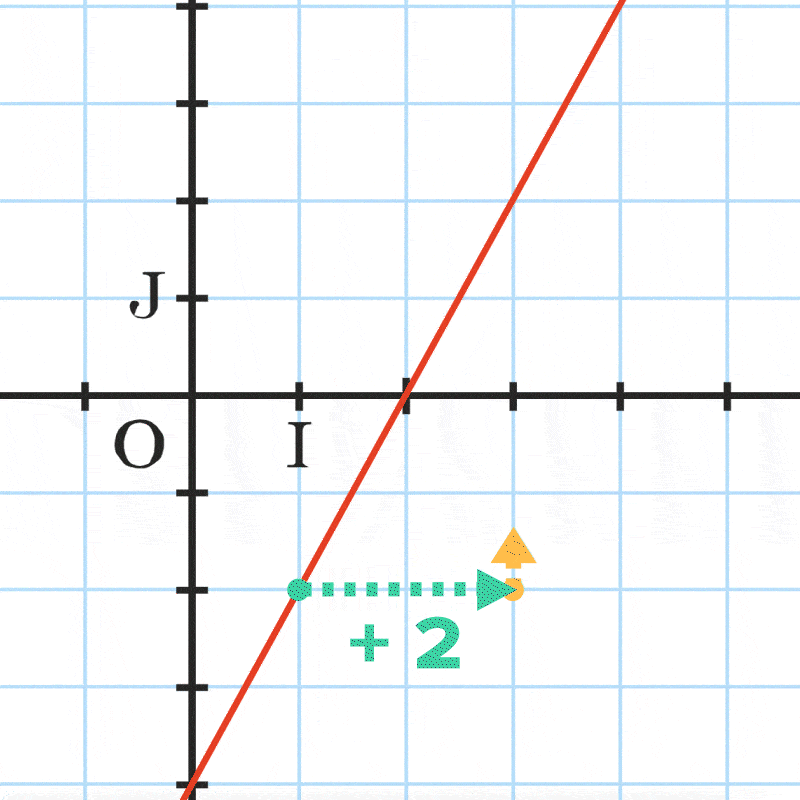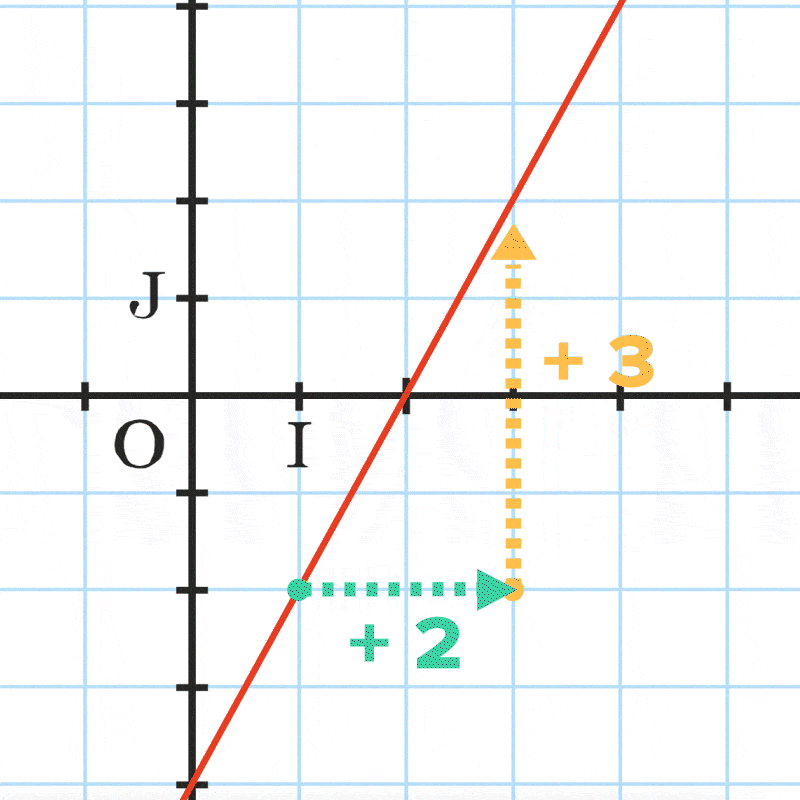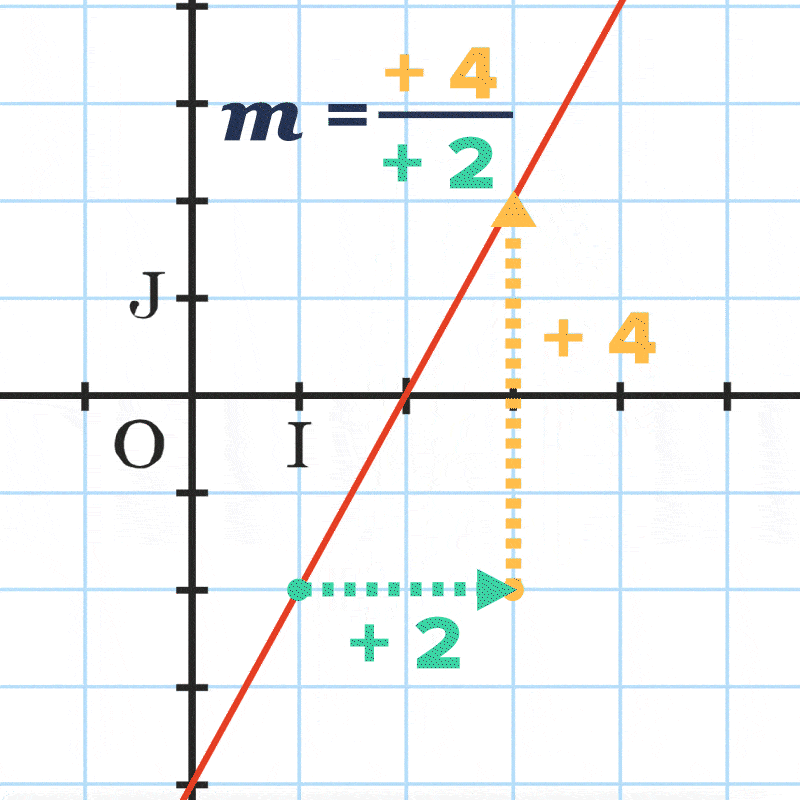
Pour représenter f, il suffit de placer deux points \mathrm{A}\left(x_{\mathrm{A}} \:; y_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}} \:; y_{\mathrm{B}}\right) avec y_{\mathrm{A}}=m x_{\mathrm{A}}+p \text { et } y_{\mathrm{B}}=m x_{\mathrm{B}}+p puis de tracer la droite passant par ces deux points.

La différence des ordonnées de \mathrm{A} et \mathrm{B} est proportionnelle à la différence des abscisses de \mathrm{A} et \mathrm{B}.

• Pour placer les deux points \text {A} et \text {B}, on choisit deux abscisses x_{\mathrm{A}} et x_{\mathrm{B}}.
• On calcule les ordonnées y_{\mathrm{A}}=m x_{\mathrm{A}}+p et y_{\mathrm{B}}=m x_{\mathrm{B}}+p.
• La droite (\mathrm{AB}) est la courbe représentative de la fonction affine.