1. Reconnaître la représentation graphique des fonctions de référence.
2. Comparer l'image de deux nombres par ces fonctions.
3. Résoudre graphiquement ou algébriquement équations et inéquations faisant intervenir ces fonctions.
4. Utiliser la position relative de leur courbe représentative.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

La forme de cette toupie rappelle celle de la fonction inverse. Son énergie de rotation dépend du carré de sa vitesse de rotation. La fonction inverse et la fonction carré sont deux des quatre fonctions de référence qui sont étudiées dans ce chapitre.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Avant de commencer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Prérequis

1. Utiliser les identités remarquables usuelles.
2. Maîtriser les notions d'image et d'antécédent.
3. Dresser graphiquement un tableau de variations ou le lire.
4. Utiliser la définition de fonction croissante ou décroissante.
5. Déterminer graphiquement la position relative de courbes.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Anecdote

La somme des inverses des carrés de tous les entiers naturels non nuls est égale à \dfrac { \pi ^ { 2 } } { 6 } : \dfrac { 1 } { 1 ^ { 2 } } + \dfrac { 1 } { 2 ^ { 2 } } + \dfrac { 1 } { 3 ^ { 2 } } + \ldots = \dfrac { \pi ^ { 2 } } { 6 }.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Utiliser une représentation graphique

On considère la courbe représentative d'une fonction f définie sur [ - 2\:; 4 ].

1. Déterminer les images de 0 ; –1 et 3 par f .

2. Déterminer un antécédent de 4, deux antécédents de 3, un antécédent de 1 et deux antécédents
de 2 par f .

3. Donner un exemple de réel qui possède trois antécédents par f .

4. Donner un exemple de réel qui ne possède pas d'antécédent par f .

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Développer et factoriser une expression

Soit x \in \mathbb { R } .
1. Développer et réduire les expressions suivantes.
a. ( 2 x + 1 ) ^ { 2 }

b. ( x + 4 ) ( x - 4 )

c. ( 3 x - 4 ) ^ { 2 }

2. Factoriser les expressions suivantes.
a. x ^ { 2 } - 2 x + 1

b. 4 x ^ { 2 } + 12 x + 9

c. 4 x ^ { 2 } - 9

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Lire et utiliser des variations

On donne la courbe représentative d'une fonction g définie sur l'intervalle \mathrm { I } = [ 0\:; 5 ].

1. La fonction g est-elle monotone sur \mathrm { I }\:?

2. Dresser le tableau de variations de g sur \mathrm { I }.

3. a. Donner le sens de variation de g sur l'intervalle [ 3\:; 4 ].

b. On suppose que a et b appartiennent à [ 3\:; 4 ] tels que a \lt b. Comparer g(a) et g(b).

4. Répondre aux questions 3. a. et 3. b. sur l'intervalle [ 2\:; 3 ].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Lire et utiliser un tableau de variations

On donne ci-après le tableau de variations d'une fonction f définie sur [ - 10\:; 9 ].

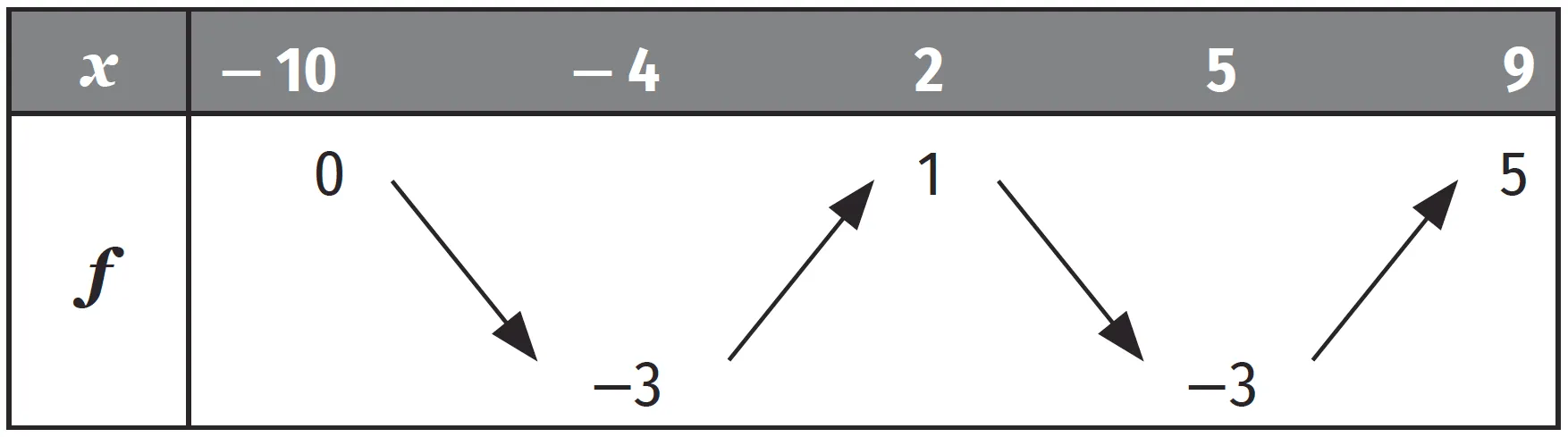
1. Tracer la courbe représentative d'une fonction ayant ce tableau de variations.

2. Compléter avec les symboles \lt ou \gt. Écrire « ? » si on ne peut pas savoir.
a. f ( 6 )

f ( 8 )

b. f ( - 3\text{,}6 )

( 1\text{,}3 )

c. f ( - 6 )

f ( - 2 )

d. f ( - 8 )

f ( - 5 )

e. f ( 3\text{,}2 )

f ( 5\text{,}72 )

f. f ( 2\text{,}01 )

f ( 2\text{,}1 )

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Problème

Un particulier possède un terrain sur lequel il veut installer un potager rectangulaire \mathrm { ABCD }.
Pour ne pas être dérangé par des animaux nuisibles, il souhaite le clôturer avec un grillage.
Il veut avoir un potager de 25 m² et minimiser la longueur de grillage à utiliser. 1. On note x la longueur \mathrm { AB } en m.
a. Quelles sont les valeurs possibles de x\:?

b. Exprimer, en fonction de x, la longueur \mathrm{BC}.

2. Exprimer, en fonction de x, le périmètre \mathrm { P } ( x ) du potager.

3. Tracer la courbe représentative de \mathrm { P } et en déduire son tableau de variations.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

Cliquez pour accéder à une zone de dessin

4. a. Pour quelle valeur de x le périmètre est-il minimal ?

b. Quelle est alors la valeur de ce périmètre ?

c. Quelle est la particularité de \mathrm { ABCD }\:?

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Fonctions de référence

Rappels de collège

Vidéo « À quoi ça sert les maths ? »

Capacités attendues

Avant de commencer

Prérequis

Anecdote

1 Utiliser une représentation graphique

2 Développer et factoriser une expression

3 Lire et utiliser des variations

4Lire et utiliser un tableau de variations

5Problème

GeoGebra

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

1
Utiliser une représentation graphique

2
Développer et factoriser une expression

3
Lire et utiliser des variations

4
Lire et utiliser un tableau de variations

5
Problème