Mathématiques 2de
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 4
Cours 1
Fonction carré, fonction racine carrée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AFonction carré
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
- La fonction carré est la fonction qui, à tout réel x, associe le réel x ^ { 2 }.
- Sa courbe représentative est une parabole.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
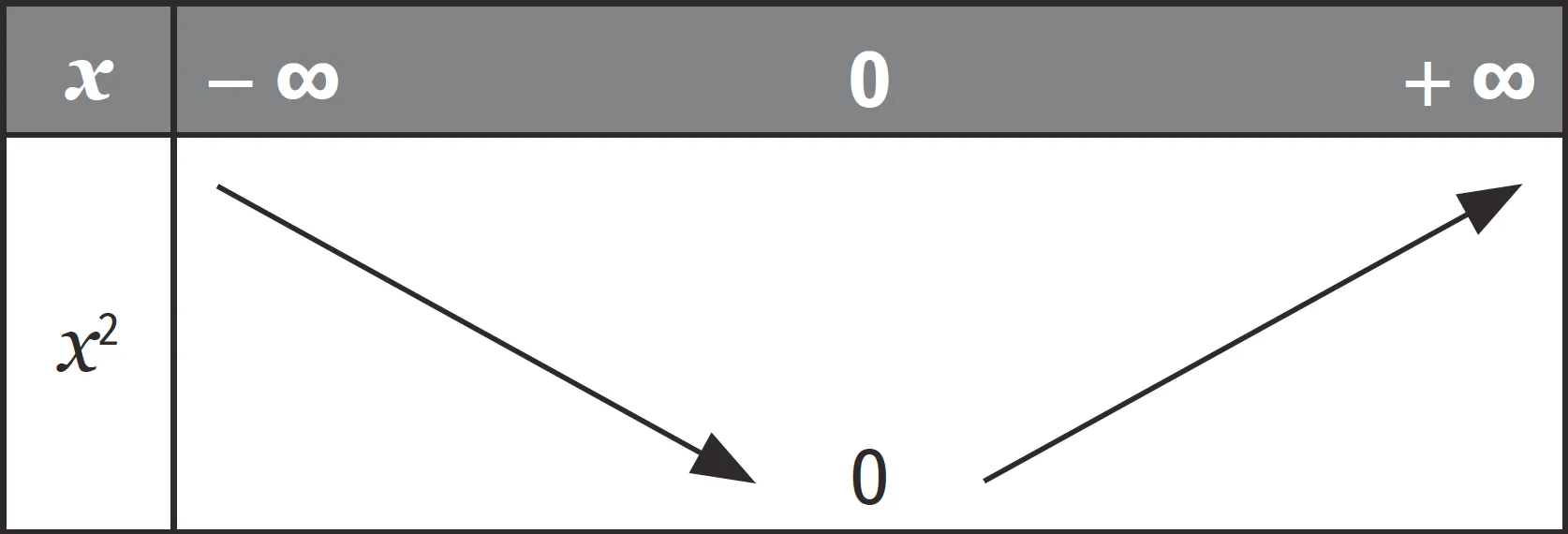
Propriété
1. Pour tout réel x , x ^ { 2 } \geqslant 0.
2. La fonction carré est paire.
3. La fonction carré est strictement décroissante sur ] - \infty\:; 0 ] et strictement croissante sur [ 0\:; + \infty [.
1. Le produit de deux nombres réels de même signe est positif donc x \times x est positif.
2. Pour tout x \in \mathbb { R }, ( - x ) ^ { 2 } = ( - x ) \times ( - x ) = x ^ { 2 } donc l'image de -x est égale à l'image de x donc la fonction carré est paire.
3. Voir exercice p. 133.
2. La fonction carré est paire.
3. La fonction carré est strictement décroissante sur ] - \infty\:; 0 ] et strictement croissante sur [ 0\:; + \infty [.
Démonstration
1. Le produit de deux nombres réels de même signe est positif donc x \times x est positif.
2. Pour tout x \in \mathbb { R }, ( - x ) ^ { 2 } = ( - x ) \times ( - x ) = x ^ { 2 } donc l'image de -x est égale à l'image de x donc la fonction carré est paire.
3. Voir exercice p. 133.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction carré est paire donc sa courbe représentative admet un axe de symétrie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Genially
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Compléter avec \lt , \gt ou = sans calculatrice.
1. 1\text{,}125 ^ { 2 } \ldots 1\text{,}13 ^ { 2 }
2. ( - 3\text{,}21 ) ^ { 2 } \ldots ( - 2 ) ^ { 2 }
3. ( - 3 ) ^ { 2 } \ldots 3 ^ { 2 }
4. \pi ^ { 2 } \ldots 3 ^ { 2 }
5. ( - 999 ) ^ { 2 } \ldots ( - 1\,000 ) ^ { 2 }
1. 1\text{,}125 ^ { 2 } \ldots 1\text{,}13 ^ { 2 }
2. ( - 3\text{,}21 ) ^ { 2 } \ldots ( - 2 ) ^ { 2 }
3. ( - 3 ) ^ { 2 } \ldots 3 ^ { 2 }
4. \pi ^ { 2 } \ldots 3 ^ { 2 }
5. ( - 999 ) ^ { 2 } \ldots ( - 1\,000 ) ^ { 2 }
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On utilise les variations de la fonction carré :
- Si a \lt b \leqslant 0 , a ^ { 2 } \gt b ^ { 2 } car la fonction est strictement décroissante sur {] - \infty\:; 0 ]}, l'ordre change.
- Si 0 \leqslant a \lt b , a ^ { 2 } \lt b ^ { 2 } car la fonction est strictement croissante sur {[ 0\:; + \infty [}, l'ordre est conservé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BFonction racine carrée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
- Pour tout réel positif x, la racine carrée de x est le nombre positif, noté \sqrt { x }, tel que ( \sqrt { x } ) ^ { 2 } = x.
- La fonction racine carrée est la fonction qui, à tout réel positif x, associe le réel \sqrt { x }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les propriétés de calculs sur les racines carrées sont indiquées dans la partie page 19.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
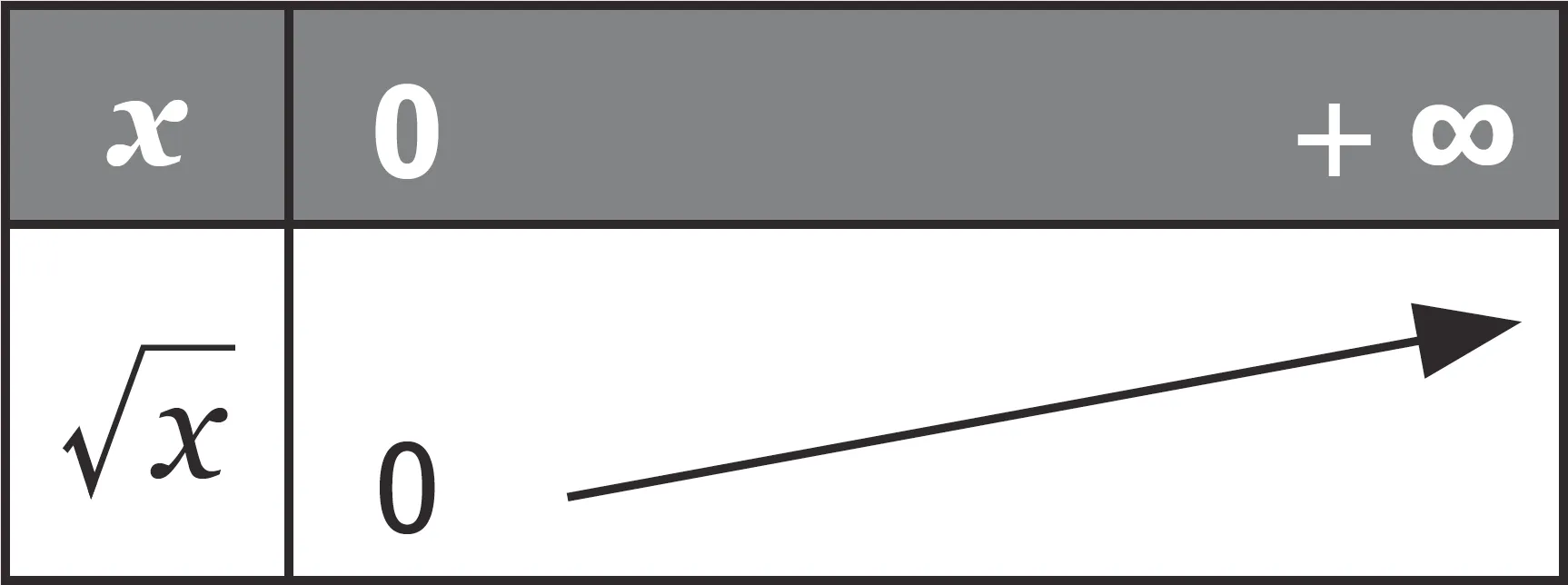
Propriété
1. On a : \sqrt { 0 } = 0 et, pour tout x \gt 0, \sqrt { x } \gt 0.
2. La fonction racine carrée est strictement croissante sur [ 0\:; + \infty [.
3. Pour tous réels positifs a et b, \sqrt { a \times b } = \sqrt { a } \times \sqrt { b }. De plus, si b \neq 0 alors \sqrt { \dfrac { a } { b } } = \dfrac { \sqrt { a } } { \sqrt { b } }.
2. La fonction racine carrée est strictement croissante sur [ 0\:; + \infty [.
3. Pour tous réels positifs a et b, \sqrt { a \times b } = \sqrt { a } \times \sqrt { b }. De plus, si b \neq 0 alors \sqrt { \dfrac { a } { b } } = \dfrac { \sqrt { a } } { \sqrt { b } }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
1. L'équation y ^ { 2 } = 0 possède une unique solution y = 0 donc \sqrt { 0 } = 0.
Soit x \geqslant 0. Par définition, \sqrt { x } \geqslant 0. Mais si \sqrt { x } = 0, alors ( \sqrt { x } ) ^ { 2 } = 0 donc x = 0.
Donc, par contraposée : si x \gt 0, alors \sqrt { x } \gt 0.
2. Voir exercice p. 134
3. Voir la partie p. 19
2. Voir exercice p. 134
3. Voir la partie p. 19
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démontrer l'implication \text{A} \Rightarrow \text{B} revient à démontrer sa contraposée \text{non B} \Rightarrow \text{non A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Genially
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Déplacer le curseur pour passer de la courbe de la fonction carré à celle de la fonction racine carrée.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
1. Les écritures suivantes ont-elles un sens ? Justifier la réponse et simplifier si cela est possible.
a. \sqrt { 4 }
b. \sqrt { - 3 }
c. \sqrt { ( - 5 ) ^ { 2 } }
d. \sqrt { 121 }
e. \sqrt { 3 - \pi }
2. Compléter sans calculatrice avec \lt ou \gt.
a. \sqrt { 2 } \ldots \sqrt { 2\text{,}03 }
b. \sqrt { \dfrac { 3 } { 2 } } \ldots 1
c. \sqrt { 6 } \ldots \sqrt { 2 \pi }
a. \sqrt { 4 }
b. \sqrt { - 3 }
c. \sqrt { ( - 5 ) ^ { 2 } }
d. \sqrt { 121 }
e. \sqrt { 3 - \pi }
2. Compléter sans calculatrice avec \lt ou \gt.
a. \sqrt { 2 } \ldots \sqrt { 2\text{,}03 }
b. \sqrt { \dfrac { 3 } { 2 } } \ldots 1
c. \sqrt { 6 } \ldots \sqrt { 2 \pi }
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. La fonction racine carrée est définie sur \mathbb { R } ^ { + }. Donc, si x \lt 0, \sqrt { x } n'existe pas. \sqrt { 4 } est le nombre positif y tel que y ^ { 2 } = 4: c'est 2.
2. La fonction racine carrée est strictement croissante sur \mathbb { R } ^ { + } donc si 0 \leqslant a \lt b , alors \sqrt { a } \lt \sqrt { b } l'ordre est conservé.
2. La fonction racine carrée est strictement croissante sur \mathbb { R } ^ { + } donc si 0 \leqslant a \lt b , alors \sqrt { a } \lt \sqrt { b } l'ordre est conservé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. a. 2
b. Impossible car -3 \lt 0
c. 5
d. 11
e. Impossible car 3 - \pi \lt 0
2. La fonction racine carrée est strictement croissante sur \mathbb { R } ^ { + } donc :
a. \sqrt { 2 } \lt \sqrt { 2\text{,}03 } car 2 \lt 2\text{,}03
b. \sqrt { \dfrac { 3 } { 2 } } > 1 car \dfrac { 3 } { 2 } > 1
c. \sqrt { 6 } \lt \sqrt { 2 \pi } car 6 \lt 2 \pi
b. Impossible car -3 \lt 0
c. 5
d. 11
e. Impossible car 3 - \pi \lt 0
2. La fonction racine carrée est strictement croissante sur \mathbb { R } ^ { + } donc :
a. \sqrt { 2 } \lt \sqrt { 2\text{,}03 } car 2 \lt 2\text{,}03
b. \sqrt { \dfrac { 3 } { 2 } } > 1 car \dfrac { 3 } { 2 } > 1
c. \sqrt { 6 } \lt \sqrt { 2 \pi } car 6 \lt 2 \pi
Pour s'entraîner
Exercices p. 131, et p. 133
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
