1. Tracer la courbe représentative de la fonction a. Pour ce faire, on entrera la commande : a(x) = abs(x).

2. Vérifier que les valeurs trouvées dans la première question préliminaire sont correctes en tapant : a(5), a(-6), etc.

3. Définir les fonctions c et r en tapant : c(x) = x ^ 2 et r(x) = sqrt(x).

4. Supprimer l'affichage des courbes représentatives des fonctions c et r en cliquant sur les disques de couleur.


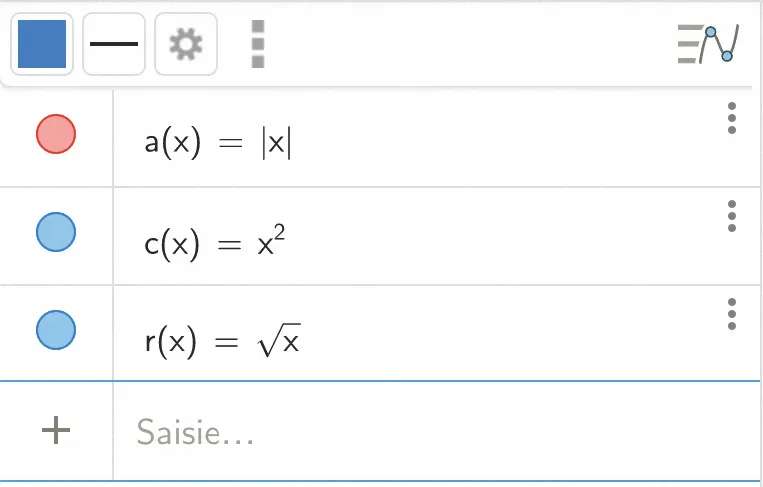
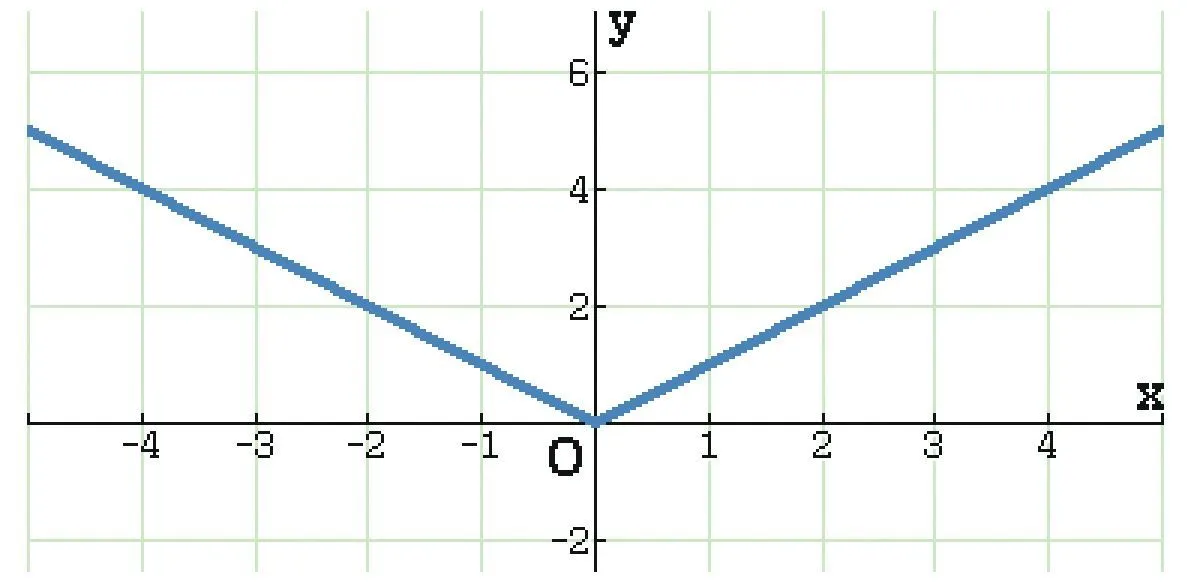
5. Tracer la courbe représentative de la fonction définie sur Geogebra par f(x) = r(c(x)). Que remarque-t-on ? En déduire une nouvelle expression de |x|.

Dans cette partie, nous allons observer que l'on peut donner une expression de a à partir de c et de r en comparant deux tableaux de valeurs.

1. À l'aide de l'outil abs de la calculatrice, vérifier que les résultats de la question préliminaire sont corrects.

2. Entrer la fonction a dans la calculatrice, ainsi que la fonction x \mapsto \sqrt { x ^ { 2 } }.

3. Avec les outils de la calculatrice, afficher un tableau de valeurs en commençant à -2 avec un pas de 0{,}5 puis compléter le tableau suivant.

4. Afficher la table des deux fonctions et en déduire que l'on semble avoir | x | = \sqrt { x ^ { 2 } } pour tout x \in \mathbb { R }.

5. Renforcer cette conjecture en traçant le graphe des deux fonctions.