Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de soci été
Chapitre 4
TP / TICE 2
Vers la racine cubique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Pour tout a \in \mathbb { R }, la racine cubique de a est l'unique réel x solution de l'équation x^3 = a . Souvent, ce nombre est irrationnel et ne peut donc pas s'écrire comme une fraction d'entiers. On cherche donc ici à donner une approximation \sqrt [ 3 ] { a }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Utiliser des outils numériques afin de donner une approximation du
nombre \sqrt [ 3 ] { a } ( a \in \mathbb { R } ) avec une des deux méthodes de résolution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Geogebra
1. Ouvrir GeoGebra et entrer la fonction f(x) = x ^ 3.
Le zoom est accessible dans la version Premium.
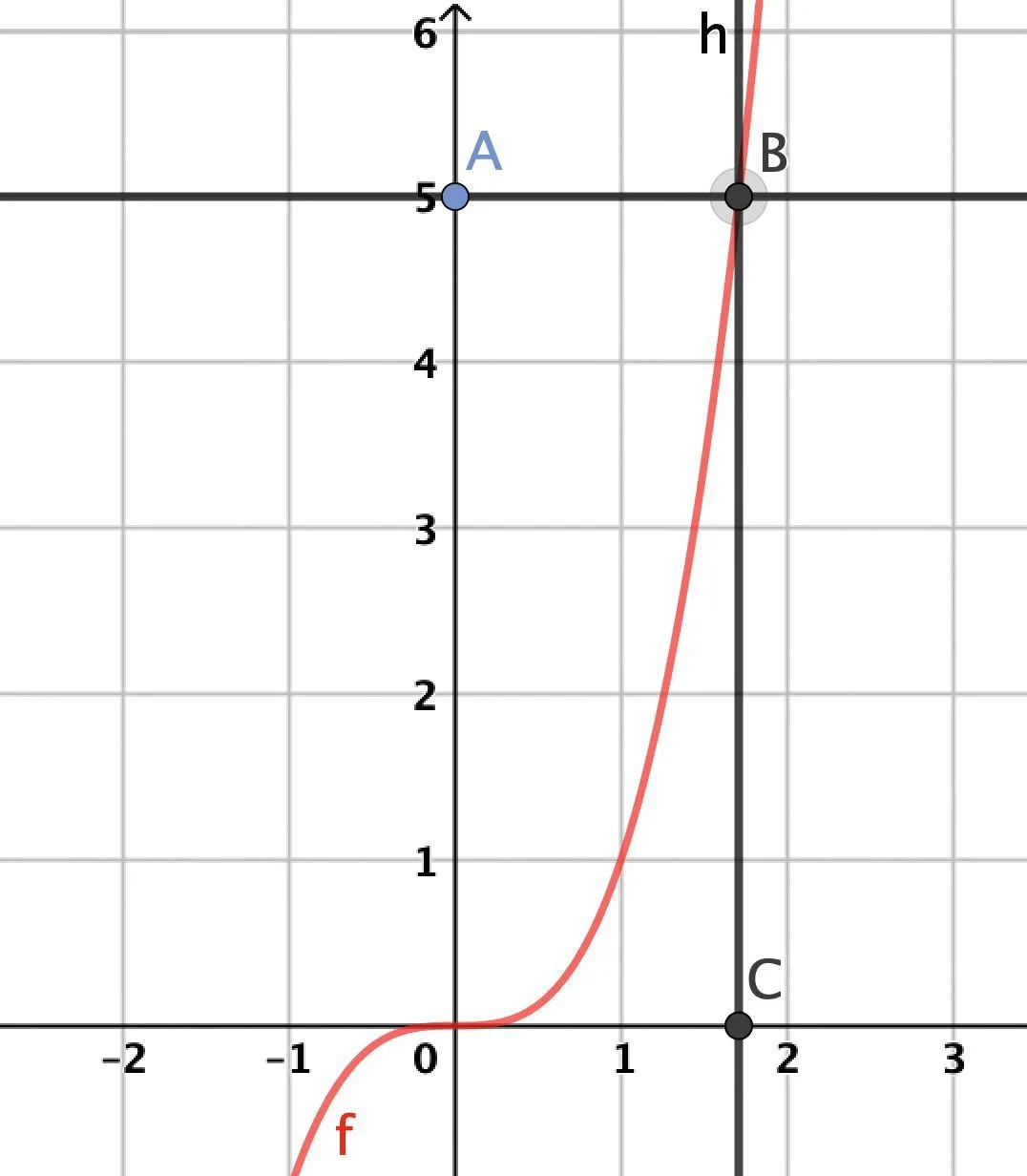
2. On choisit le réel a = 5. Placer le point \text{A} de coordonnées (0\:; 5) grâce à la commande : \text{A} = (0{,}5).
3. Sélectionner l'outil Parallèle, cliquer sur le point \text{A} puis sur l'axe des abscisses. Avec l'outil Point, placer le point \text{B}, intersection de la droite tracée avec la courbe représentative de f .
4. Tracer la droite parallèle à l'axe des ordonnées et passant par \text{B.} Placer \text{C} le point d'intersection de cette droite avec l'axe des abscisses.
5. Justifier que l'abscisse de \text{C} est égale à \sqrt [ 3 ] { 5 }.
6. Cliquer sur Options › Arrondi › 10 décimales. En déduire une valeur approchée de \sqrt [ 3 ] { 5 } à 10^{-10} près.
3. Sélectionner l'outil Parallèle, cliquer sur le point \text{A} puis sur l'axe des abscisses. Avec l'outil Point, placer le point \text{B}, intersection de la droite tracée avec la courbe représentative de f .
4. Tracer la droite parallèle à l'axe des ordonnées et passant par \text{B.} Placer \text{C} le point d'intersection de cette droite avec l'axe des abscisses.
5. Justifier que l'abscisse de \text{C} est égale à \sqrt [ 3 ] { 5 }.
6. Cliquer sur Options › Arrondi › 10 décimales. En déduire une valeur approchée de \sqrt [ 3 ] { 5 } à 10^{-10} près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On calcule ensuite : x _ { 1 } = \dfrac { 2 x _ { 0 } + \dfrac { a } { \left( x _ { 0 } \right) ^ { 2 } } } { 3 } et on continue : x _ { 2 } = \dfrac { 2 x _ { 1 } + \dfrac { a } { \left( x _ { 1 } \right) ^ { 2 } } } { 3 }, etc.
1. Reproduire la feuille de calcul ci-dessous.
Le zoom est accessible dans la version Premium.
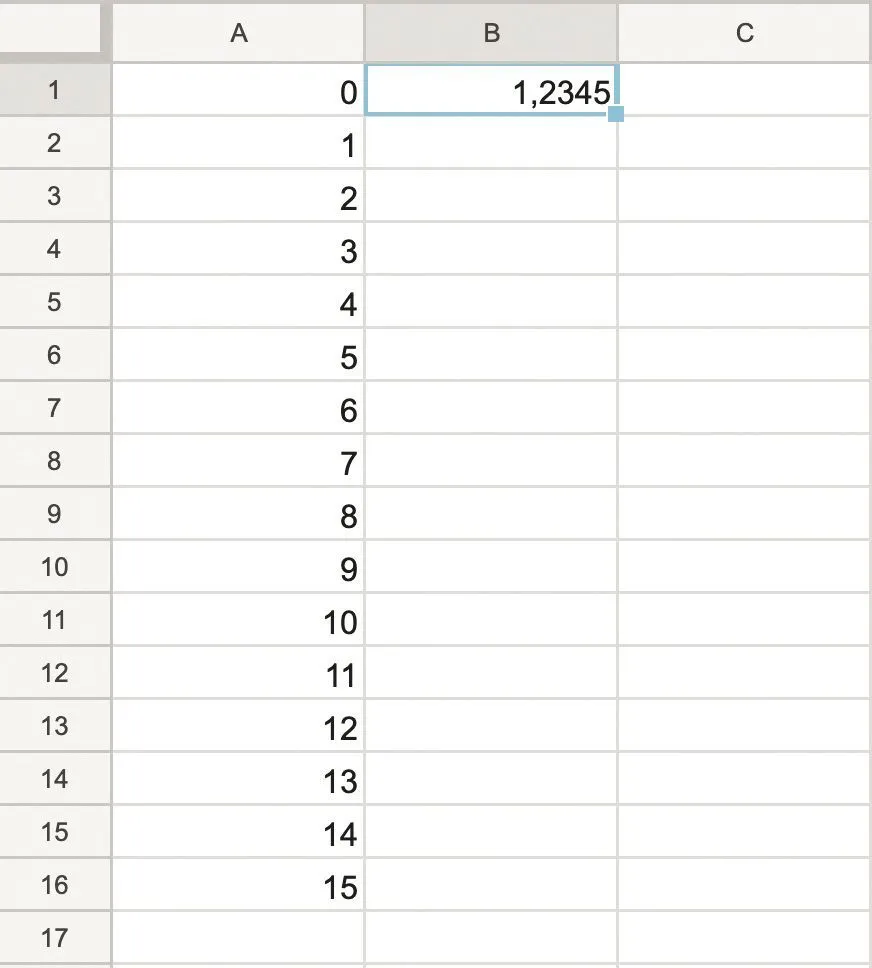
2. Dans la cellule B2, entrer : = (2 * \text{B}1 + 5/(\text{B}1 ^ 2))/3. Étirer cette formule jusqu'à la cellule B16.
3. Dans la cellule C1, entrer : = \text{B}1 ^ 3. Étirer cette formule jusqu'à la cellule C16.
4. Expliquer la colonne B et la colonne C.
5. Que se passe-t-il lorsqu'on change la valeur de B1 ? Donner une valeur approchée de \sqrt [ 3 ] { 5 } à 10^{-10} près.
3. Dans la cellule C1, entrer : = \text{B}1 ^ 3. Étirer cette formule jusqu'à la cellule C16.
4. Expliquer la colonne B et la colonne C.
5. Que se passe-t-il lorsqu'on change la valeur de B1 ? Donner une valeur approchée de \sqrt [ 3 ] { 5 } à 10^{-10} près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Programmer l'algorithme de Héron avec Python et comparer les résultats obtenus.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah