Partie 4
Histoire des mathématiques
Statistiques et probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire Histoire des nombres et racine carrée
Les plus vieilles traces de recensements (population, bétail, cultures) remontent au XXIIIe siècle av. J.-C. Le premier écrit statistique est à attribuer à Al-Kindi (Irak, 801-873) : le manuscrit sur le déchiffrement de messages cryptographiques explique comment procéder pour décrypter un texte codé à partir du chiffre de César (permutation des lettres de l'alphabet) en analysant les fréquences d'apparition des lettres du texte chiffré. Ces méthodes auraient été utilisées pour décrypter les messages des Croisés. Il a fallu attendre le XVIIe siècle avec le développement des probabilités ainsi que de nouveaux besoins économiques (assurances), industriels (erreurs de typographie, nettoyage des cuves de bière) et médicaux (vaccinations) pour voir l'essor de cette discipline.


Extrait du Risalah fi Istikhraj al-Mu'amma (manuscrit sur le déchiffrement de messages cryptographiques).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireNaissance des probabilités et problème du chevalier de Méré

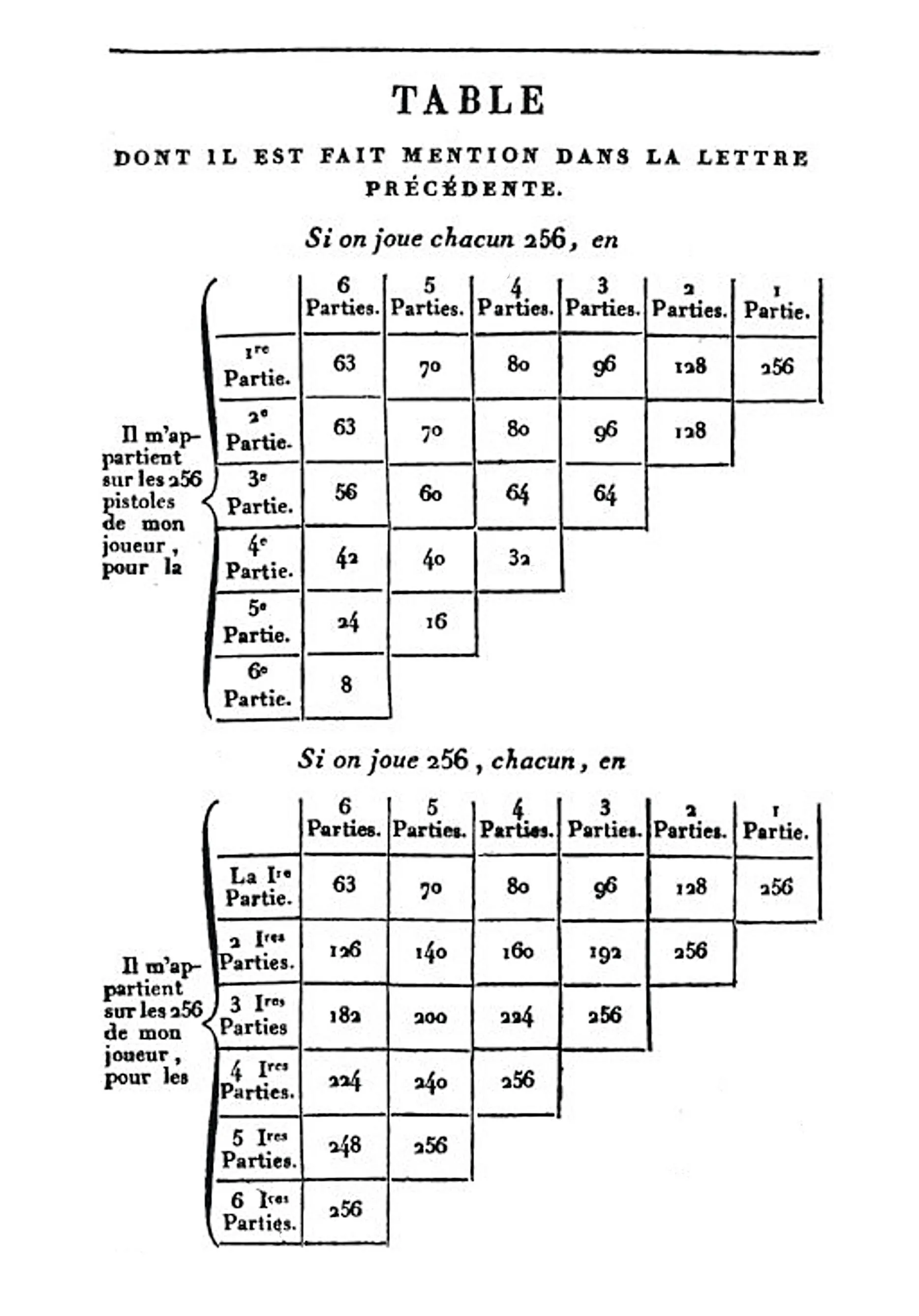
Extrait des échanges entre Pascal et Fermat, 1654.
Le chevalier de Méré (17e siècle) était un joueur et souhaitait connaître les stratégies amenant à un plus grand nombre de succès. Il soumet ce problème : « Deux joueurs misent chacun 32 pistoles dans un jeu en trois manches gagnantes. La partie est interrompue alors que le premier joueur a remporté deux manches et le second une seule. Quel doit être alors le gain de chacun des deux joueurs ? » Pascal et Fermat relèvent le défi et on retrouve les réponses dans leurs échanges épistolaires.


Le problème décrit par le chevalier de Méré est un problème historique que l'on trouve déjà dans le Summa de Arithmetica de Luca Pacioli (1494). Pascal et Fermat sont les premiers à y apporter une solution mathématique généralisable.
C'est cependant le Hollandais Christiaan Huygens (1629-1695) qui publie en 1657 le premier traité mathématique consacré aux probabilités : Tractatus de Rariociniis in Alea Ludo. De nos jours, les probabilités constituent une partie très importante des mathématiques.


Le problème décrit par le chevalier de Méré est un problème historique que l'on trouve déjà dans le Summa de Arithmetica de Luca Pacioli (1494). Pascal et Fermat sont les premiers à y apporter une solution mathématique généralisable.
C'est cependant le Hollandais Christiaan Huygens (1629-1695) qui publie en 1657 le premier traité mathématique consacré aux probabilités : Tractatus de Rariociniis in Alea Ludo. De nos jours, les probabilités constituent une partie très importante des mathématiques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question
Un autre problème porte le nom de paradoxe du chevalier de Méré : « Est-il plus facile d'obtenir un six en quatre lancers de dés que d'avoir un double six en lançant 24 fois deux dés ? ».
Comment résoudre cette question ?
Comment résoudre cette question ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

