Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 9
TP / TICE
Taux moyen annuel
18 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans un pays, le ministère des Finances a augmenté
les impôts sur les revenus sur une période de
5 années en utilisant chaque année le même taux
d'évolution.
Un foyer qui payait 950 € d'impôt en 2012, en payait
1 140 € en 2017.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
On cherche à calculer le taux d'augmentation annuel moyen (à 0,001 % près), c'est-à-dire le taux d'évolution qui a été appliqué chaque année, en utilisant une des deux méthodes.
Objectif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. Calculer le taux d'évolution global entre 2012 et
2017 pour ce foyer.
2. Justifier que le problème se ramène à chercher le taux annuel t tel que (1+t)^{5}=1\text{,}20.
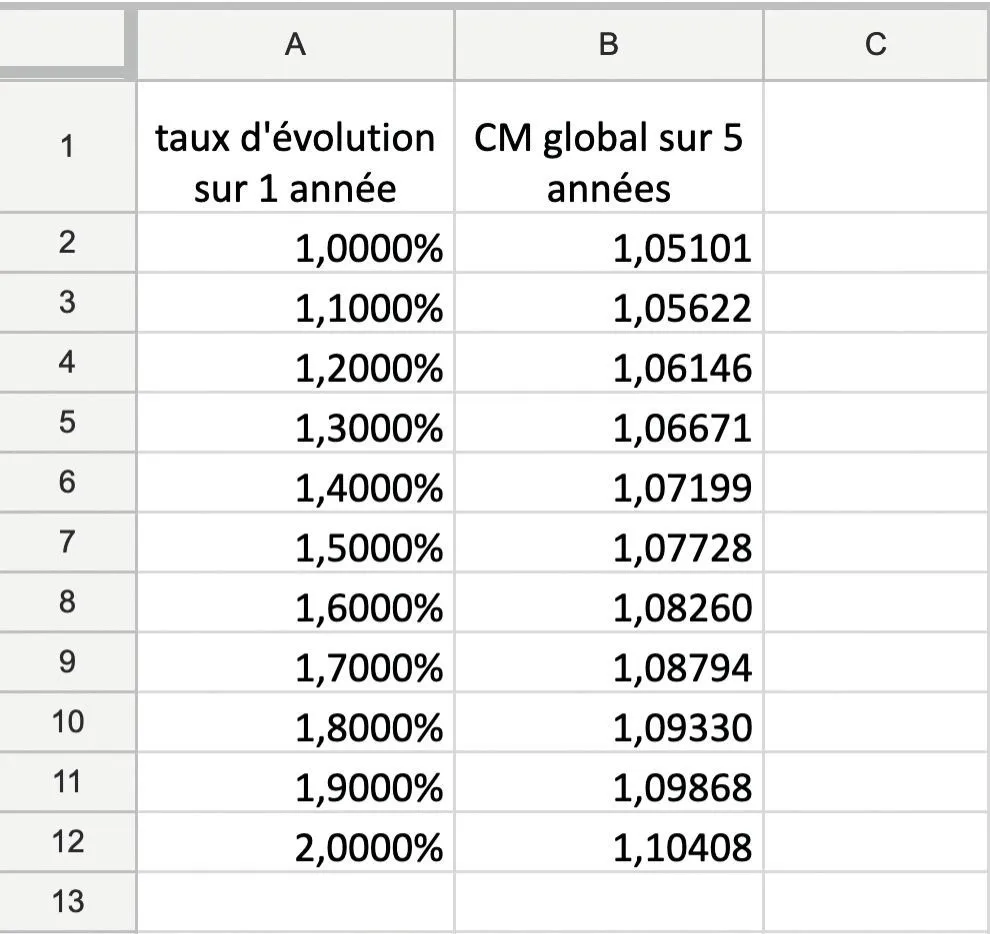
3. Quelle formule entrée en B2 permet de calculer le coefficient multiplicateur global associé à 5 hausses de l'évolution donnée en A2 ?
4. Avec un pas de 0,1 % pour t , recopier la formule trouvée ci-dessus puis donner un encadrement du taux d'évolution moyen recherché à 10-1 près.
5. Recommencer ensuite avec un taux d'évolution compris dans l'encadrement trouvé ci-dessus mais avec un pas de 0,01 % puis de 0,001 %, pour enfin conclure.
2. Justifier que le problème se ramène à chercher le taux annuel t tel que (1+t)^{5}=1\text{,}20.
3. Quelle formule entrée en B2 permet de calculer le coefficient multiplicateur global associé à 5 hausses de l'évolution donnée en A2 ?
4. Avec un pas de 0,1 % pour t , recopier la formule trouvée ci-dessus puis donner un encadrement du taux d'évolution moyen recherché à 10-1 près.
5. Recommencer ensuite avec un taux d'évolution compris dans l'encadrement trouvé ci-dessus mais avec un pas de 0,01 % puis de 0,001 %, pour enfin conclure.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2GeoGebra
1. Justifier que le problème se ramène à résoudre l'équation 1\,140 = 950 \times (1 + x)^{5} .
2. À l'aide de la partie calcul formel de GeoGebra, résoudre l'équation et donner la réponse à la question. Arrondir à 0,001 % près.
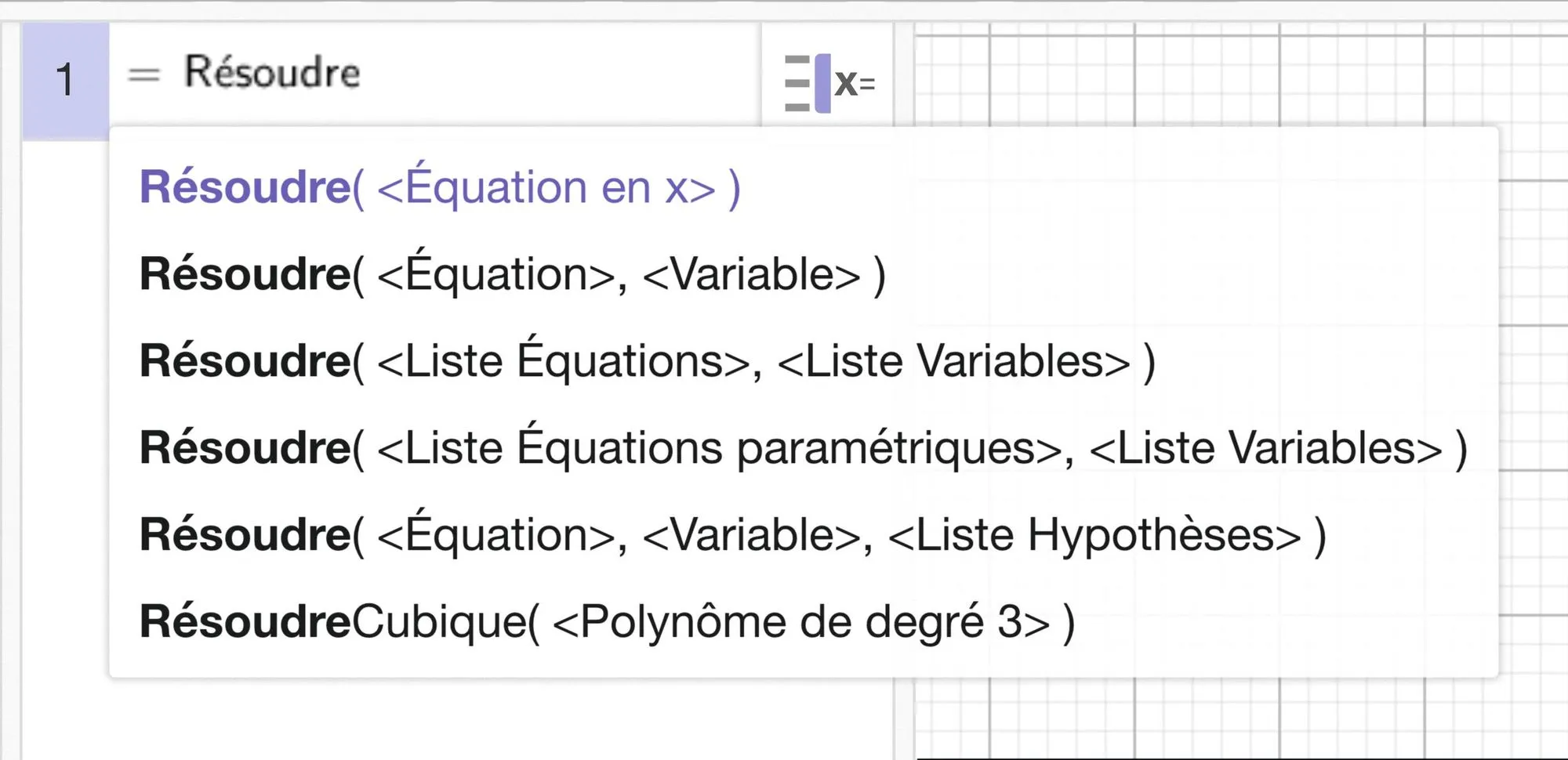
3. Tracer la courbe de la fonction x \mapsto 950 \times(1+x)^{5} et retrouver la réponse à la question précédente.
2. À l'aide de la partie calcul formel de GeoGebra, résoudre l'équation et donner la réponse à la question. Arrondir à 0,001 % près.
Le zoom est accessible dans la version Premium.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pendant x années, le même taux d'évolution t
(positif ou négatif) est appliqué chaque année
à une valeur de départ connue \text{V}_{\text{D}} . On connaît
également la valeur d'arrivée \text{V}_{\text{A}} .
Réaliser une feuille de calcul permettant de retrouver systématiquement une valeur approchée de t à 10-2 près lorsqu'on donne des valeurs fixées à x , \text{V}_{\text{D}} et \text{V}_{\text{A}}.
Réaliser une feuille de calcul permettant de retrouver systématiquement une valeur approchée de t à 10-2 près lorsqu'on donne des valeurs fixées à x , \text{V}_{\text{D}} et \text{V}_{\text{A}}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah