72
[Calculer.]
Certaines plantes vertes peuvent voir leur croissance augmenter rapidement. Une variété grandit de 60 % en 3 mois puis de 50 % les 3 mois suivants.

Déterminer le taux de croissance sur 6 mois de cette variété de plante verte.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

73
[Calculer.]

La population d'une ville de 45 304 habitants augmente de 5 % puis diminue de 10 % l'année suivante.

1. Calculer le taux d'évolution global sur les deux années.

2. Calculer le nombre d'habitants après ces évolutions. Arrondir à l'entier le plus proche.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

74
[Calculer.]

De juin à août, le temps perdu dans les embouteillages à Paris durant les heures de pointe diminue en moyenne de 80 % puis augmente de 275 % en septembre pour atteindre 15 secondes perdues par kilomètre parcouru (source : Étude V-Traffic).

Combien de temps est perdu en moyenne par kilomètre par un automobiliste en juin ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

75
[Modéliser.]
Lors de l'achat d'une voiture, le vendeur propose une remise de 10 % sur le prix HT puis d'appliquer la TVA de 20 %. Le client préférerait que le vendeur lui applique la remise de 10 % sur le prix TTC.

La proposition du client lui est-elle plus avantageuse ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

76
[Calculer.]

En 2015, il y a eu 17 268 immatriculations de voitures électriques. Ce nombre a augmenté de 44,26 % en 2 ans dont 25,96 % la première année (source : Fiches-auto.fr).

Déterminer le taux d'évolution du nombre d'immatriculations de voitures électriques de 2016 à 2017. Arrondir à 0,01 % près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

77
[Calculer.]
Lors des premières représentations d'un jeune humoriste, le nombre de spectateurs fluctue fortement. Il a baissé les 15 premiers jours du mois puis a augmenté de 35 % les 15 derniers jours.

Sachant que le nombre de spectateurs a augmenté de 25 % entre le premier et le dernier jour de ce mois de représentation, déterminer le taux d'évolution la première quinzaine, arrondi à 0,01 % près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

78
[Calculer.]
Le prix moyen d'une baguette de pain en euros par kg a augmenté de 0,87 % de 2011 à 2015 puis de 0,57 % de 2015 à 2017. 1. Calculer le taux d'évolution global entre 2011 et 2017. Arrondir à 0,01 % près.

2. Que remarque-t-on si l'on additionne les deux taux d'évolutions successifs ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

79
[Modéliser.]
Lucas place ses économies de 520 € sur un compte à intérêts composés au taux annuel de 2,25 %. Autrement dit, les intérêts sont calculés chaque année à partir du nouveau montant total.
Déterminer le montant présent sur son compte, au centime près : 1. 2 ans plus tard ;

2. 3 ans plus tard.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

80
[Calculer.]
Déterminer le taux d'évolution global associé à trois baisses successives de 42 %, arrondi à 0,01 % près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

81
[Calculer.]
Le prix d'un baril de pétrole a augmenté de 7,34 % entre août et septembre, puis a augmenté de 9,78 % en octobre pour chuter ensuite de 11,46 % en novembre.
Déterminer le taux d'évolution global du prix d'un baril de pétrole entre août et novembre.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

82
Tableur
[Calculer.]
Le tableau ci-après donne les taux d'évolution successifs du nombre d'objets connectés dans le monde entre les années 2011 et 2015.
La cellule B6 est au format pourcentage écrit avec une décimale (source : IDATE DigiWorld, Institut de l'audiovisuel et des télécoms en Europe).

Le zoom est accessible dans la version Premium.

1. Quelle formule faut-il entrer en C3 puis recopier vers la droite pour calculer le coefficient multiplicateur associé aux taux d'évolution du dessus ?

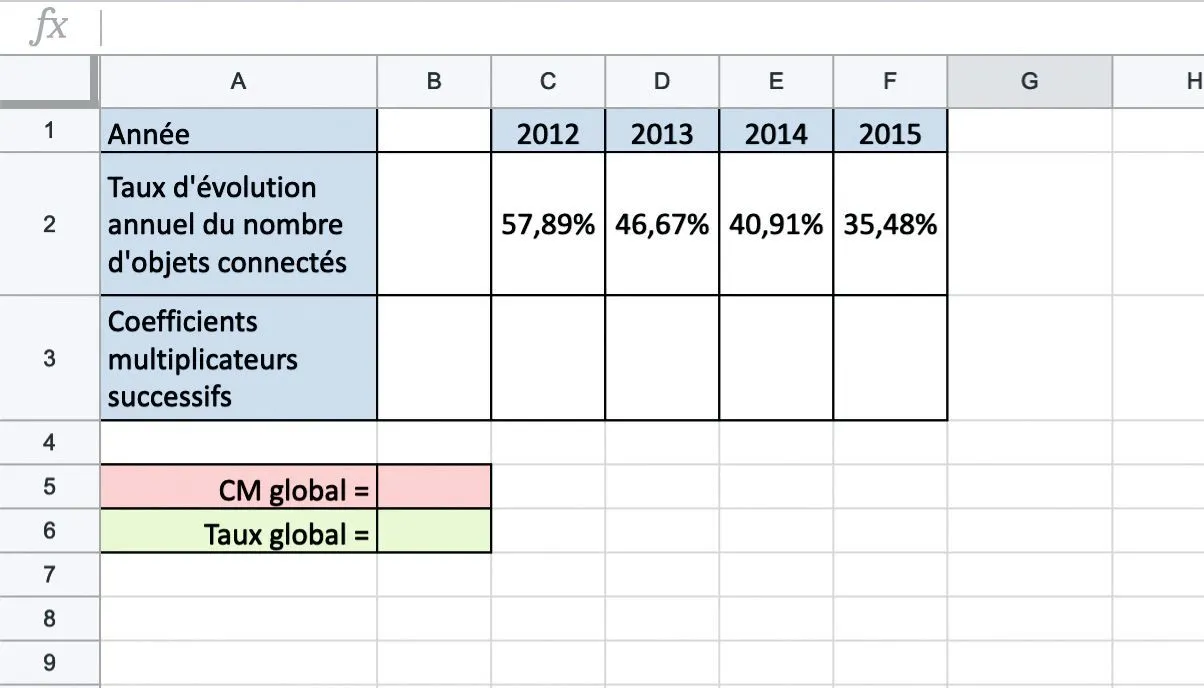
2. Quelles formules faut-il entrer en B5 et B6 pour calculer le coefficient multiplicateur global et le taux d'évolution global ?

3. Recopier et compléter le tableau dans un tableur.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

83
Python
[Modéliser.]
Le programme ci-dessous, écrit en Python, permet de calculer le pourcentage d'évolution global, connaissant les deux pourcentages d'évolutions successives p_{1} et p_{2} .

def Taux_global (p1, p2):
  CM1 = 1+p1/100
  CM2 = 1+p2/100
  CM = ....
  p = .....
  return(p)
print (Taux_global(24,-35))

1. Expliquer pourquoi, dans les lignes 2 et 3, on divise p_{1} et p_{2} par 100.

2. Compléter les lignes 4 et 5.

3. Tester ce programme avec p_{1} = 24 et p_{2} = -35.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

84
[Calculer.]

Suite à son passage en machine à laver, un pull a rétréci de 7 %. En utilisant des astuces pour récupérer sa taille d'origine, de quel pourcentage (à 0,1 % près) doit-il alors s'agrandir ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

85
[Calculer.]

Après une augmentation de ses prix de 11,3 % puis de 5,7 %, un commerçant souhaite récompenser un client fidèle en lui accordant une remise telle qu'elle compense ses deux dernières augmentations.

Déterminer le pourcentage de remise que doit effectuer le commerçant.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

86
[Chercher.]

Lors d'une période de promotion, on peut lire sur les vitrines d'un magasin d'ameublement :

Le zoom est accessible dans la version Premium.

1. Pour une cuisine destinée à un logement neuf et affichée à 7 540 € TTC, quel sera le prix payé par le client avec cette remise, au centime d'euros près ?

2. De quelle remise (à 0,01 % près), le client a-t-il réellement profité ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

87
[Raisonner.]
Étienne se plaint car Justine gagne 66,7 % de plus que lui. Pour le rassurer, Jimmy lui dit qu'il ne gagne que 40 % de moins que Justine. Étienne doit-il se sentir rassuré ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

88
[Chercher.]
Une action en Bourse a connu les évolutions suivantes au cours des 7 dernières heures : +3 % ; +1,2 % ; -4,5 % ; +0,2 % ; -5,6 % ; -1 % ; +0,7 %. À la fin de la 8^e heure, le taux d'évolution global est finalement de +0,3 %.
Quel a été le taux d'évolution entre la 7^e et la 8^e heure ? Arrondir à 0,1 % près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

89
[Chercher.]

Lundi, Audrey possède une certaine somme d'argent \text{S} dans sa tirelire. Mardi, elle ajoute 40 % de cette somme, mercredi, elle ajoute 30 % de la nouvelle somme dans sa tirelire. Puis, jeudi, elle ajoute 20 % de la nouvelle somme. Enfin, elle ajoute 10 % du total de sa tirelire le vendredi. Le samedi, elle décide de dépenser tout l'argent qu'elle a ajouté et sa tirelire dispose à nouveau de la somme de départ \text{S}.

Le zoom est accessible dans la version Premium.

1. Quel a été le taux global d'augmentation de la somme \text{S} entre lundi et vendredi ?

2. Quel a été le taux réciproque le samedi ? Arrondir à 0,1 % près.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.