Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 5
Cours 2
Distance dans un repère orthonormé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADistance entre deux points
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Dans un repère orthonormé du plan, la distance entre deux points \text{A} et \text{B} de coordonnées respectives \left(x_{\mathrm{A}}\:; y_{\mathrm{A}}\right) et \left(x_{\mathrm{B}}\:; y_{\mathrm{B}}\right) est donnée par :
\mathrm{AB}=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}}.
\mathrm{AB}=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
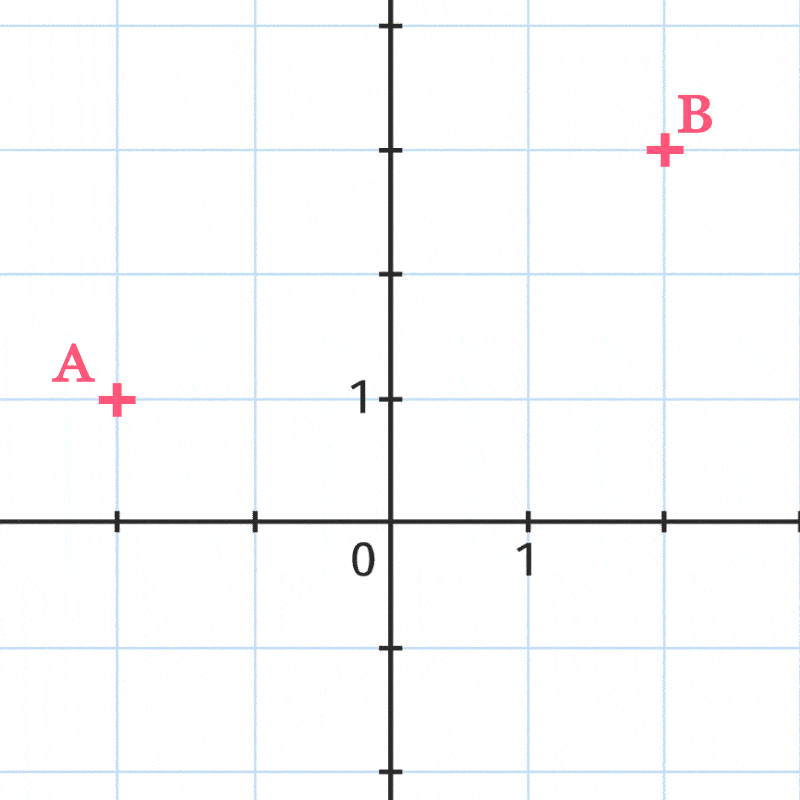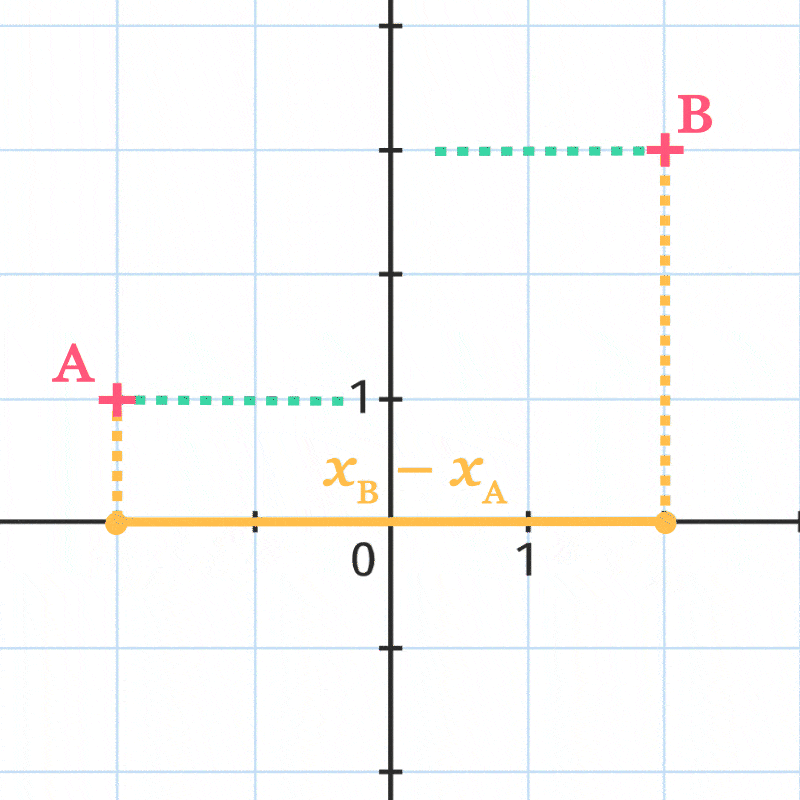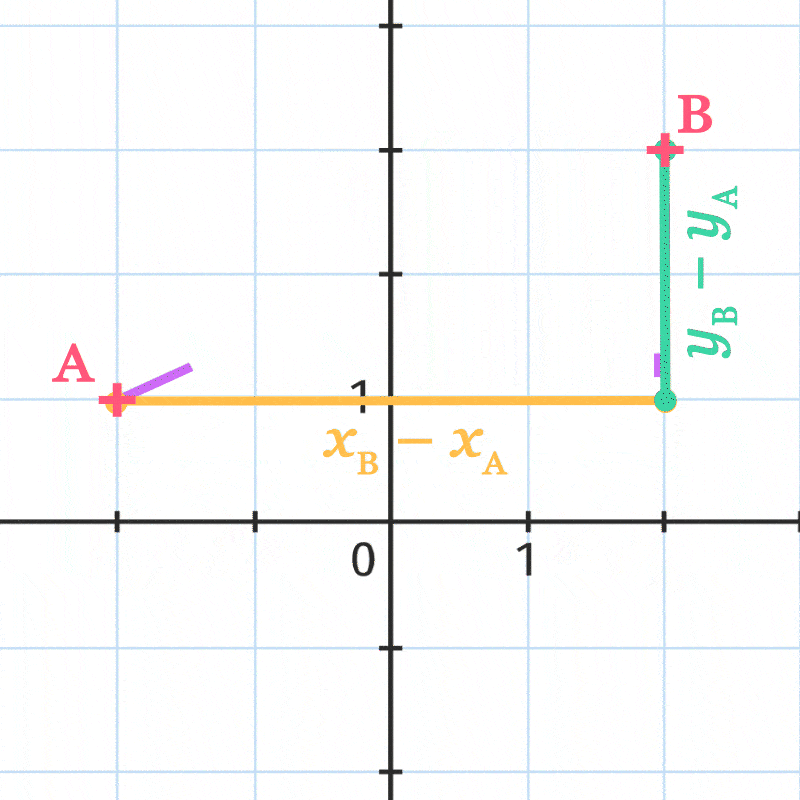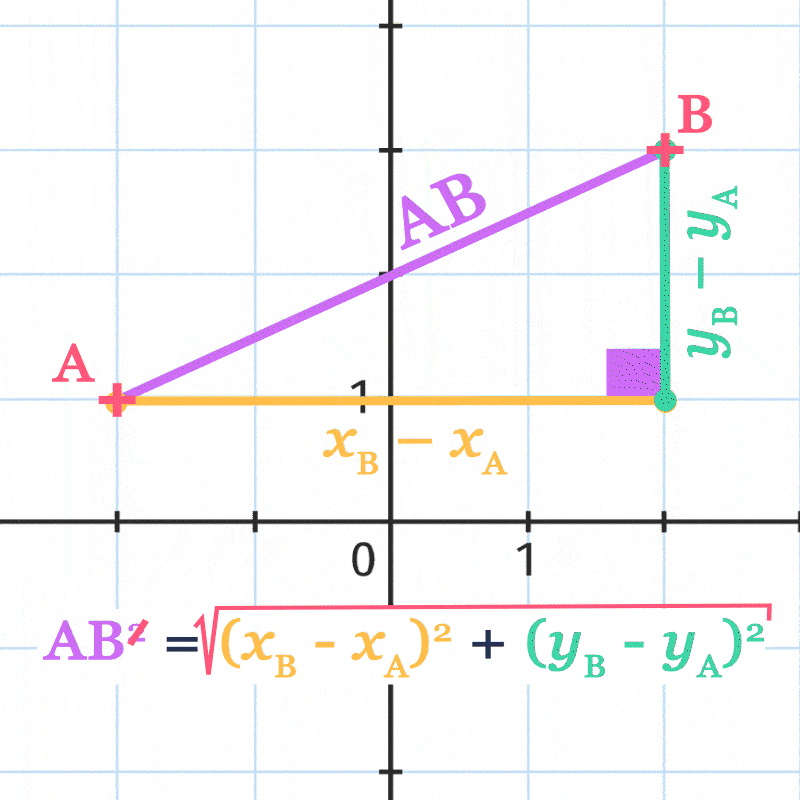
Démonstration
On traite le cas où x_{\mathrm{B}}>x_{\mathrm{A}} et y_{\mathrm{B}}>y_{\mathrm{A}}.
On considère le point \text{C} de coordonnées \left(x_{\mathrm{B}} \: ; y_{\mathrm{A}}\right). Les axes du repère sont perpendiculaires donc le triangle \text{ABC} est rectangle en \text{C} .
D'après le théorème de Pythagore :
\mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BC}^{2}.
Or, \mathrm{AC}=x_{\mathrm{C}}-x_{\mathrm{A}}=x_{\mathrm{B}}-x_{\mathrm{A}} et
\mathrm{BC}=y_{\mathrm{B}}-y_{\mathrm{C}}=y_{\mathrm{B}}-y_{\mathrm{A}} donc
\mathrm{AB}^{2}=\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}.
\text{AB} étant une longueur, \text{AB} est un nombre positif donc
\mathrm{AB}=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}}.
Les autres cas se traitent de manière similaire.
On considère le point \text{C} de coordonnées \left(x_{\mathrm{B}} \: ; y_{\mathrm{A}}\right). Les axes du repère sont perpendiculaires donc le triangle \text{ABC} est rectangle en \text{C} .
D'après le théorème de Pythagore :
\mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BC}^{2}.
Or, \mathrm{AC}=x_{\mathrm{C}}-x_{\mathrm{A}}=x_{\mathrm{B}}-x_{\mathrm{A}} et
\mathrm{BC}=y_{\mathrm{B}}-y_{\mathrm{C}}=y_{\mathrm{B}}-y_{\mathrm{A}} donc
\mathrm{AB}^{2}=\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}.
\text{AB} étant une longueur, \text{AB} est un nombre positif donc
\mathrm{AB}=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}}.
Les autres cas se traitent de manière similaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut généraliser cette preuve pour les autres cas possibles :
x_{\mathrm{B}}>x_{\mathrm{A}} et y_{\mathrm{B}}\lt x_{\mathrm{A}}, etc.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans un repère orthonormé, avec \mathrm{A}(-1\:; 2) et \text{B}(4\:; 3), on a :
\begin{aligned}\text{AB}&=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}\\&=\sqrt{(4-(-1))^{2}+(3-2)^{2}}=\sqrt{25+1}=\sqrt{26}.\end{aligned}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Déplacez les points \text{A} et \text{B} pour voir la distance entre ces deux points changer.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans un repère orthonormé (\text{O ; I , J}) du plan, on considère les points \text{A , B , C }et \text{M} de coordonnées respectives (-2\:; 3),(3\:; 4),(3\:;-2) et (1\:; 1).
Montrer que \text{A , B} et \text{C} appartiennent à un même cercle de centre \text{M}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Vérifier que le repère est orthonormé.
2. Calculer \mathrm{MA}^{2}, \mathrm{MB}^{2} et \mathrm{MC}^{2} en utilisant les coordonnées des points.
3. En déduire les distances \text{MA , MB} et \text{MC}.
4. Conclure.
2. Calculer \mathrm{MA}^{2}, \mathrm{MB}^{2} et \mathrm{MC}^{2} en utilisant les coordonnées des points.
3. En déduire les distances \text{MA , MB} et \text{MC}.
4. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Remarque : Comme on travaille sur des longueurs positives, il suffit de comparer les carrés.Le repère (\text{O ; I , J}) étant orthonormé, on a :
\mathrm{MA}^{2}=\left(x_{\mathrm{A}}-x_{\mathrm{M}}\right)^{2}+\left(y_{\mathrm{A}}-y_{\mathrm{M}}\right)^{2}=(-2-1)^{2}+(3-1)^{2}=13\:;
\mathrm{MB}^{2}=\left(x_{\mathrm{B}}-x_{\mathrm{M}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{M}}\right)^{2}=(3-1)^{2}+(4-1)^{2}=13\:;
\mathrm{MC}^{2}=\left(x_{\mathrm{C}}-x_{\mathrm{M}}\right)^{2}+\left(y_{\mathrm{C}}-y_{\mathrm{M}}\right)^{2}=(3-1)^{2}+(-2-1)^{2}=13
\mathrm{MA}^{2}=\mathrm{MB}^{2}=\mathrm{MC}^{2} donc \mathrm{MA}=\mathrm{MB}=\mathrm{MC} et les points \text{A , B} et \text{C} sont donc sur le cercle de centre \text{M} et de rayon r=\sqrt{13}
Pour s'entraîner
exercices et p. 159
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BAlignement de trois points
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient \text{A , B} et \text{C} , trois points distincts du plan. Les points \text{A , B} et \text{C} sont alignés dans cet ordre si et seulement si \mathrm{AC}=\mathrm{AB}+\mathrm{BC}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
D'après l'inégalité triangulaire, on a forcément \mathrm{AC} \leqslant \mathrm{AB}+\mathrm{BC}.
Si \text{A , B} et \text{C} sont alignés, alors le triangle \text{ABC} est plat et \text{AC} = \text{AB} + \text{BC}.
Réciproquement, si \text{AC} = \text{AB} + \text{BC} alors on obtient un triangle plat donc \text{A , B} et \text{C} sont alignés.
Si \text{A , B} et \text{C} sont alignés, alors le triangle \text{ABC} est plat et \text{AC} = \text{AB} + \text{BC}.
Réciproquement, si \text{AC} = \text{AB} + \text{BC} alors on obtient un triangle plat donc \text{A , B} et \text{C} sont alignés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans un repère orthonormé (\text{O ; I , J}), les points \text{A}(-2\:;-2), \text{B}(3\:; 1) et \text{C}(8\:; 4) sont-ils alignés ?
Le repère étant orthonormé, on a :
\begin{aligned}\mathrm{AC}&=\sqrt{(8-(-2))^{2}+(4-(-2))^{2}}\\ &=\sqrt{100+36}\\ &=\sqrt{136}=2 \sqrt{34}\end{aligned}
\begin{aligned}\mathrm{AB}&=\sqrt{(3-(-2))^{2}+(1-(-2))^{2}}\\ &=\sqrt{25+9}=\sqrt{34}\\\end{aligned}
\begin{aligned}\mathrm{BC}&=\sqrt{(8-3)^{2}+(4-1)^{2}}\\ &=\sqrt{25+9}=\sqrt{34}\end{aligned}
\mathrm{AC}=\mathrm{AB}+\mathrm{BC} donc les points \text{A} , \text{B} et \text{C} sont alignés dans cet ordre.
Le repère étant orthonormé, on a :
\begin{aligned}\mathrm{AC}&=\sqrt{(8-(-2))^{2}+(4-(-2))^{2}}\\ &=\sqrt{100+36}\\ &=\sqrt{136}=2 \sqrt{34}\end{aligned}
\begin{aligned}\mathrm{AB}&=\sqrt{(3-(-2))^{2}+(1-(-2))^{2}}\\ &=\sqrt{25+9}=\sqrt{34}\\\end{aligned}
\begin{aligned}\mathrm{BC}&=\sqrt{(8-3)^{2}+(4-1)^{2}}\\ &=\sqrt{25+9}=\sqrt{34}\end{aligned}
\mathrm{AC}=\mathrm{AB}+\mathrm{BC} donc les points \text{A} , \text{B} et \text{C} sont alignés dans cet ordre.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans cet exemple, le point \text{B} est le milieu du segment [\mathrm{AC}] puisque les points \text{A, B} et \text{C} sont alignés et que \text{AB} = \text{BC} .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Déplacez le curseur pour déplacer le point \text{C} et vérifier quand ce-dernier est aligné avec \text{A} et \text{B}.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans le repère orthonormé (\text{A ; I , J}), on considère la figure ci-dessous composée d'un carré \text{ABCD} et de deux points \text{E} et \text{F} . Les points \text{E , C} et \text{F} sont-ils alignés ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Vérifier que le repère est bien orthonormé.
2. Calculer les trois distances \text{EF} , \text{EC} et \text{CF} avec la formule de la distance entre deux points.
3. Comparer la plus grande distance avec la somme des deux autres.
2. Calculer les trois distances \text{EF} , \text{EC} et \text{CF} avec la formule de la distance entre deux points.
3. Comparer la plus grande distance avec la somme des deux autres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Dans le repère (\text{A ; I , J}), on relève les coordonnées des 6 points de la figure :
\mathrm{A}(0\:; 0), \mathrm{B}(8\:; 0), \mathrm{C}(8\:; 8), \mathrm{D}(0\:; 8), \mathrm{E}(0\:; 13) et \mathrm{F}(21\:; 0).
Le repère (\text{A ; I , J}) étant orthonormé, on a :
\mathrm{EF}=\sqrt{(21-0)^{2}+(0-13)^{2}}=\sqrt{610}\:;
\mathrm{EC}=\sqrt{(8-0)^{2}+(8-13)^{2}}=\sqrt{89}\:;
\mathrm{CF}=\sqrt{(21-8)^{2}+(0-8)^{2}}=\sqrt{233}.
\mathrm{EF}^{2} \neq(\mathrm{EC}+\mathrm{CF})^{2} donc \mathrm{EF} \neq \mathrm{EC}+\mathrm{CF} donc les points \text{E} , \text{C} et \text{F} ne sont pas alignés.
\mathrm{A}(0\:; 0), \mathrm{B}(8\:; 0), \mathrm{C}(8\:; 8), \mathrm{D}(0\:; 8), \mathrm{E}(0\:; 13) et \mathrm{F}(21\:; 0).
Le repère (\text{A ; I , J}) étant orthonormé, on a :
\mathrm{EF}=\sqrt{(21-0)^{2}+(0-13)^{2}}=\sqrt{610}\:;
\mathrm{EC}=\sqrt{(8-0)^{2}+(8-13)^{2}}=\sqrt{89}\:;
\mathrm{CF}=\sqrt{(21-8)^{2}+(0-8)^{2}}=\sqrt{233}.
\mathrm{EF}^{2} \neq(\mathrm{EC}+\mathrm{CF})^{2} donc \mathrm{EF} \neq \mathrm{EC}+\mathrm{CF} donc les points \text{E} , \text{C} et \text{F} ne sont pas alignés.
Pour s'entraîner
exercices p. 159 et p. 164
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah