Chapitre 3
TP / TICE 1
Numération : changement de base
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Un système de numération est un procédé permettant d'écrire les entiers à l'aide d'un nombre fini de symboles.
Presque chaque civilisation a eu son système de numération. Ces derniers sont classés en trois groupes : les numérations additives (numération romaine par exemple), les numérations hybrides et les numérations de position (comme les numérations babylonienne, chinoise, ou maya).
Le système que nous utilisons est basé sur la position des chiffres. En regroupant les unités par paquets de 10, on a défini les dizaines puis, en regroupant à nouveau les dizaines en paquets de 10, on a défini les centaines, etc.
Ainsi, on écrit 2 \: 358 = 2 \times 10^3 + 3 \times 10^2 + 5 \times 10^1 + 8 \times 10^0. C'est le système décimal (ou système en base 10).
Il existe d'autres bases de numération. Parmi elles, on peut noter le système sexagésimal (en base 60) dans la numération babylonienne, le système vigésimal (en base 20) dans la numération maya. Actuellement, le système binaire (en base 2) et le système hexadécimal (en base 16) sont utilisés en électronique et en informatique.
Par exemple, en informatique, le bit est une information qui ne prend que deux valeurs notées 0 ou 1. Et comme tout entier s'écrit comme une somme de puissances de 2 de façon unique, le nombre 21 s'écrit en base 2 : \overline{{\color{darkorange}1}{\color{royalblue}0}{\color{darkred}1}{\color{lightseagreen}0}{\color{purple}1}}^2.
En effet, 21 = {\color{darkorange}1} \times 2^4 + {\color{royalblue}0} \times 2^3 + {\color{darkred}1} \times 2^2 + {\color{lightseagreen}0} \times 2^1 + {\color{purple}1}.
Par ailleurs, l'écriture hexadécimale permet d'écrire les codes binaires de manière plus compacte et, inversement, une telle écriture est facilement convertible en binaire car 16 = 2^4.
Presque chaque civilisation a eu son système de numération. Ces derniers sont classés en trois groupes : les numérations additives (numération romaine par exemple), les numérations hybrides et les numérations de position (comme les numérations babylonienne, chinoise, ou maya).
Le système que nous utilisons est basé sur la position des chiffres. En regroupant les unités par paquets de 10, on a défini les dizaines puis, en regroupant à nouveau les dizaines en paquets de 10, on a défini les centaines, etc.
Ainsi, on écrit 2 \: 358 = 2 \times 10^3 + 3 \times 10^2 + 5 \times 10^1 + 8 \times 10^0. C'est le système décimal (ou système en base 10).
Il existe d'autres bases de numération. Parmi elles, on peut noter le système sexagésimal (en base 60) dans la numération babylonienne, le système vigésimal (en base 20) dans la numération maya. Actuellement, le système binaire (en base 2) et le système hexadécimal (en base 16) sont utilisés en électronique et en informatique.
Par exemple, en informatique, le bit est une information qui ne prend que deux valeurs notées 0 ou 1. Et comme tout entier s'écrit comme une somme de puissances de 2 de façon unique, le nombre 21 s'écrit en base 2 : \overline{{\color{darkorange}1}{\color{royalblue}0}{\color{darkred}1}{\color{lightseagreen}0}{\color{purple}1}}^2.
En effet, 21 = {\color{darkorange}1} \times 2^4 + {\color{royalblue}0} \times 2^3 + {\color{darkred}1} \times 2^2 + {\color{lightseagreen}0} \times 2^1 + {\color{purple}1}.
Par ailleurs, l'écriture hexadécimale permet d'écrire les codes binaires de manière plus compacte et, inversement, une telle écriture est facilement convertible en binaire car 16 = 2^4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
À l'aide d'une des deux méthodes, passer du système de numération décimal à un système en base b où b est un entier naturel supérieur ou égal à 2. Un entier n est écrit en base b lorsqu'on a trouvé :
Les nombres a_i sont les chiffres de n dans la base b.
- un entier naturel i ;
- i + 1 nombres entiers naturels a_0 \: ; a_1 \: ; \dots \: ; a_i tous strictement inférieurs à b tels que n=a_ib^{i}+a_{i-1} b^{i-1}+\ldots+a_1 b+a_0.
Les nombres a_i sont les chiffres de n dans la base b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
Étude théorique
Pour déterminer l'écriture en base b d'un nombre n, on effectue la division euclidienne de n par b qu'on écrit n=b q_{0}+r_{0}.On réitère le procédé avec q_0, c'est-à-dire qu'on écrit q_0 = bq_1 + r_1. On construit ainsi deux suites (q_n) et (r_n).
1. Montrer que la suite (q_n) est décroissante puis qu'il existe un rang n_0 tel que, pour tout n \geqslant n_0, q_n = 0 (on pourra raisonner par l'absurde).
2. On suppose que l'on a atteint le premier quotient nul. En déduire alors l'écriture du nombre n en base b et expliquer pourquoi elle est unique.
Programmation
1. Écrire un algorithme en langage Python permettant d'obtenir l'écriture en base 7 d'un nombre n écrit dans le système décimal.2. Le modifier pour écrire un nombre n du système décimal en une base b que l'on saisira en argument d'une fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On veut utiliser un tableur pour trouver les valeurs a_i de l'écriture d'un nombre n en base 7. (Fichier téléchargeable .)

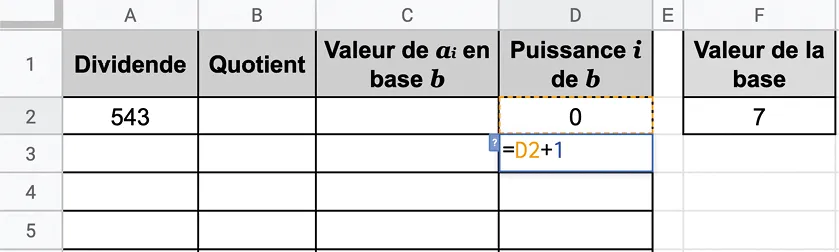
1. a. Quelles formules faut-il saisir et recopier en B2, C2 et A3 pour obtenir les valeurs a_i ?
b. Recopier les formules vers le bas jusqu'à obtenir 0 dans la colonne A.
c. En déduire l'écriture de 543 en base 7.
2. Quelles modifications faut-il apporter pour obtenir l'écriture d'un nombre n en une base b donnée en F2 ?
Tester avec l'écriture de 543 en base 8, puis dans le système binaire.


1. a. Quelles formules faut-il saisir et recopier en B2, C2 et A3 pour obtenir les valeurs a_i ?
b. Recopier les formules vers le bas jusqu'à obtenir 0 dans la colonne A.
c. En déduire l'écriture de 543 en base 7.
2. Quelles modifications faut-il apporter pour obtenir l'écriture d'un nombre n en une base b donnée en F2 ?
Tester avec l'écriture de 543 en base 8, puis dans le système binaire.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

