Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 3
TP / TICE 2
La conjecture de Syracuse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit n un entier naturel.
On considère l'algorithme suivant :
On définit ainsi une suite de nombres (\text U_n) de premier terme \text{U}_0, que l'on conjecture toujours aboutir, après un nombre fini d'opérations, à la séquence 4\:; 2\:; 1 \:;4 \:;2\:; 1\:; etc. Ce résultat n'est pas encore démontré à ce jour.
- si n est pair, on le divise par 2, c'est-à-dire que n prend la valeur \dfrac{n}{2} ;
- si n est impair, on le multiplie par 3 et on ajoute 1 au résultat, c'est-à-dire que n prend la valeur 3n + 1.
On définit ainsi une suite de nombres (\text U_n) de premier terme \text{U}_0, que l'on conjecture toujours aboutir, après un nombre fini d'opérations, à la séquence 4\:; 2\:; 1 \:;4 \:;2\:; 1\:; etc. Ce résultat n'est pas encore démontré à ce jour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Tester la conjecture de Syracuse à l'aide de l'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
1.
Montrer la conjecture dans le cas où \text{U}_{0}=4, \text{U}_{0}=2 et \text{U}_{0}=1.
2. Écrire les différentes étapes pour \text{U}_0 = 17 jusqu'à obtenir pour dernières valeurs 4 \:; 2 \:; 1.
2. Écrire les différentes étapes pour \text{U}_0 = 17 jusqu'à obtenir pour dernières valeurs 4 \:; 2 \:; 1.
3.
a. Démontrer que s'il existe un entier naturel non nul p tel que \text U_p est un multiple de 3, alors \text U_{p-1} est un multiple de 3.
b. En déduire que \text U_{p-1} est pair, puis que \text U_{0} = 2^p \text U_p.
Aide
On pourra raisonner pas contraposée et par disjonction des cas.
b. En déduire que \text U_{p-1} est pair, puis que \text U_{0} = 2^p \text U_p.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
SI (Condition ; valeur si condition vraie ; valeur si condition fausse) et que la fonction MOD(a ; b) donne le reste de la division de a par b.
On saisit une valeur de \text U_0 dans la cellule B2.
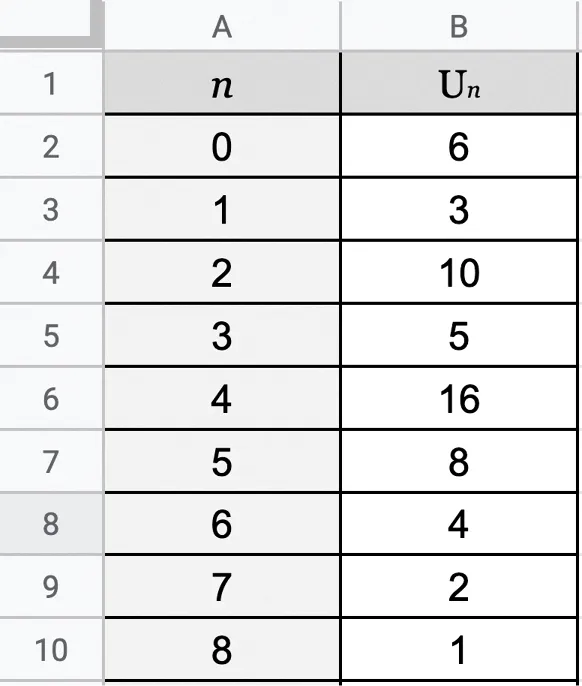
Quelle formule doit-on saisir en B3 pour obtenir dans la colonne B les valeurs de la suite de Syracuse en recopiant la cellule B3 vers le bas ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
Compléter le programme ci‑dessous prenant en entrée le premier terme \text U_0 d'une suite de Syracuse et retournant en sortie la liste des termes successifs de cette suite. On arrêtera le programme une fois la séquence 4, 2, 1 atteinte.
def syracuse(u):
L = [u]
while u != ... :
if ... :
u = u/2
L.append(u)
else:
u = ...
L.append(u)
return L
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La conjecture de Syracuse est énoncée en 1937 par
le mathématicien allemand Lothar Collatz et est
popularisée par son compatriote Helmut Hasse lors
d'un voyage à l'université de Syracuse aux États-Unis.
Elle a particulièrement mobilisé les mathématiciens
durant la guerre froide.
Si l'énoncé de la conjecture est très simple, aucune
démonstration de ce résultat n'existe à ce jour.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
