Mathématiques Expertes Terminale
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 2
TP Info 2
Ensemble de Mandelbrot
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit c un nombre complexe. On considère une suite de nombres complexes (z_n) définie sur \mathbb{N} par z_0=0 et, pour tout entier naturel n, z_{n+1}=z_{n}^{2}+c.
Pour tout entier naturel n, on note u_{n}=\left|z_{n}\right|.
L'ensemble de Mandelbrot, noté \mathcal{M}, est l'ensemble des nombres complexes c tels que la suite (u_n) est bornée.
Question préliminaire :
On note, pour tout n \in \mathbb{N}, z_{n}=x_{n}+\mathrm{i} y_{n} et c=a+\mathrm{i} b, où a, b, x_n et y_n sont des réels.
L'ensemble de Mandelbrot, noté \mathcal{M}, est l'ensemble des nombres complexes c tels que la suite (u_n) est bornée.
Question préliminaire :
On note, pour tout n \in \mathbb{N}, z_{n}=x_{n}+\mathrm{i} y_{n} et c=a+\mathrm{i} b, où a, b, x_n et y_n sont des réels.
Exprimer les termes x_{n+1} et y_{n+1} en fonction de a, b, x_n et y_n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Étudier quelques propriétés de l'ensemble de Mandelbrot à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. a. Reproduire la feuille de calcul ci‑dessous. (Fichier téléchargeable ).
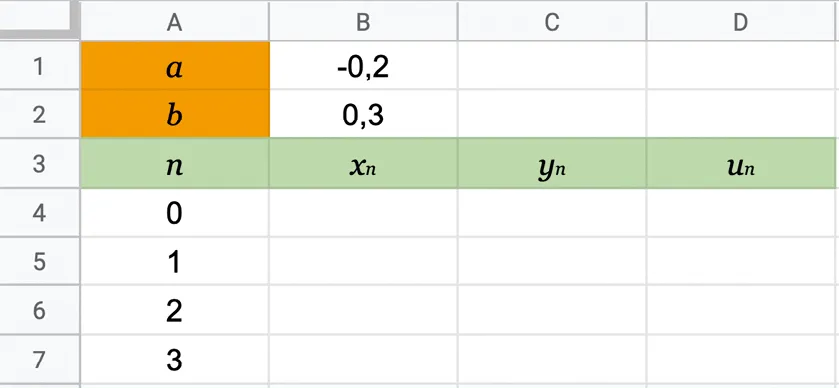
b. Quelles formules faut‑il saisir dans les cellules B4, C4, B5, C5 et D4 pour obtenir les valeurs de la suite (u_n) dans la colonne D ?
c. Obtenir les 30 premières valeurs de la suite (u_n).
2. Conjecturer l'éventuelle convergence de la suite (u_n) pour c=-0{,}2+0{,}3 \mathrm{i}.
3. Déterminer trois valeurs de c qui appartiennent à \mathcal{M}, puis trois valeurs de c qui ne lui appartiennent pas.
b. Quelles formules faut‑il saisir dans les cellules B4, C4, B5, C5 et D4 pour obtenir les valeurs de la suite (u_n) dans la colonne D ?
c. Obtenir les 30 premières valeurs de la suite (u_n).
2. Conjecturer l'éventuelle convergence de la suite (u_n) pour c=-0{,}2+0{,}3 \mathrm{i}.
3. Déterminer trois valeurs de c qui appartiennent à \mathcal{M}, puis trois valeurs de c qui ne lui appartiennent pas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
Les mathématiciens ont prouvé que, dès qu'il existe un terme de la suite (u_n) dépassant strictement 2, alors cette suite n'est pas bornée.
1. Reproduire et compléter l'algorithme suivant et expliquer l'affichage obtenu.
2. Programmer et tester cet algorithme avec Python pour les valeurs c=-0{,}2+0{,}3 \mathrm{i} et c=0{,}6+0{,}6 \mathrm{i}.
Quelles conclusions concernant l'ensemble \mathcal{M} peut‑on obtenir à l'aide de ce programme ?
1. Reproduire et compléter l'algorithme suivant et expliquer l'affichage obtenu.
\boxed{
\begin{array} { l }
\text {Fonction Mandelbrot } (a , b) : \\
\quad {x} \leftarrow {0} \\
\quad {y} \leftarrow {0} \\
\quad {n} \leftarrow {0} \\
\quad {\mathrm{U}} \leftarrow \ldots \\
\quad \text {Tant que } \mathrm{U} \leqslant 2 \text { et } n \leqslant 30 :\\
\quad \quad \mathrm{X} \leftarrow {x} \\
\quad \quad \mathrm{Y} \leftarrow {y} \\
\quad \quad {x} \leftarrow \ldots \\
\quad \quad {y} \leftarrow \ldots \\
\quad \quad {\mathrm{U}} \leftarrow \ldots \\
\quad \quad {n} \leftarrow {n+1} \\
\quad \text {Si } n=31 : \\
\quad \quad \text {Afficher « oui »} \\
\quad \text {Sinon :} \\
\quad \quad \text {Afficher « non »} \\
\end{array}
}
2. Programmer et tester cet algorithme avec Python pour les valeurs c=-0{,}2+0{,}3 \mathrm{i} et c=0{,}6+0{,}6 \mathrm{i}.
Quelles conclusions concernant l'ensemble \mathcal{M} peut‑on obtenir à l'aide de ce programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En 1980, pour la première fois, Benoît Mandelbrot parvient à représenter cet ensemble à l'aide d'un ordinateur.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
