Chapitre 6
Calcul matriciel et applications aux graphes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capacités attendues
1. Modéliser une situation par une matrice.
2. Calculer l'inverse et les puissances d'une matrice carrée.
3. Utiliser le calcul matriciel pour résoudre un système linéaire.
4. Modéliser une situation par un graphe.
5. Utiliser le calcul matriciel pour calculer le nombre de chemins de longueur donnée entre deux sommets d'un graphe.
2. Calculer l'inverse et les puissances d'une matrice carrée.
3. Utiliser le calcul matriciel pour résoudre un système linéaire.
4. Modéliser une situation par un graphe.
5. Utiliser le calcul matriciel pour calculer le nombre de chemins de longueur donnée entre deux sommets d'un graphe.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Internet est le réseau informatique mondial. Il permet aux ordinateurs du monde entier de communiquer entre eux. Ces communications sont possibles grâce à des câbles sous‑marins qui traversent les océans pour relier les continents. La théorie des graphes abordée dans ce chapitre permet de modéliser des réseaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avant de commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Prérequis
1. Utiliser un tableur.
2. Savoir résoudre un système de deux équations à deux inconnues.
3. Connaître les transformations planes.
4. Connaître le cosinus et le sinus des angles remarquables.
2. Savoir résoudre un système de deux équations à deux inconnues.
3. Connaître les transformations planes.
4. Connaître le cosinus et le sinus des angles remarquables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le théorème des quatre couleurs stipule qu'il
faut au plus quatre couleurs pour colorier
des zones sur une carte sans que deux zones
adjacentes soient coloriées de la même
couleur.
Ce problème peut être modélisé par un
graphe, dont les sommets sont les différentes
zones à colorier et les arêtes représentent les
frontières communes entre ces zones.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Utiliser un tableur
Sur la feuille de calcul ci‑dessous figurent les
compositions de quatre bouquets de fleurs ainsi
que le prix unitaire par fleur.

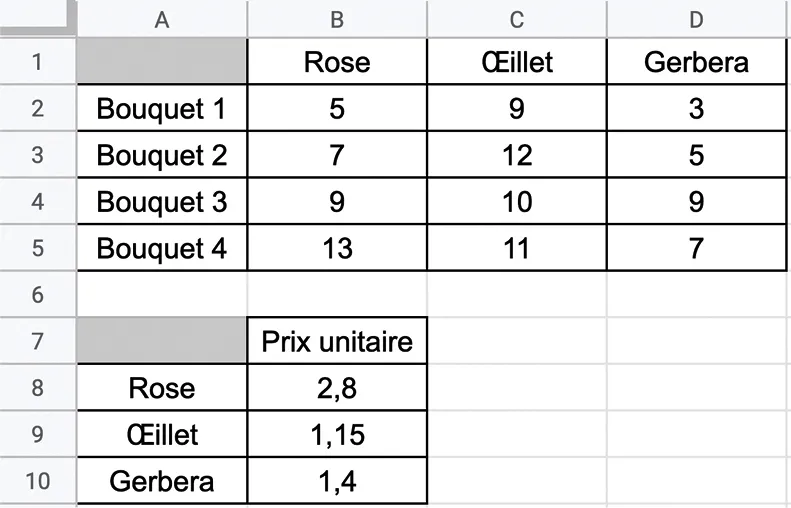
1. a. Calculer à la main le nombre total de fleurs de chaque sorte en regroupant les quatre bouquets.
b. Quelle formule de calcul doit‑on écrire en B6 et étendre vers la droite pour calculer ce total ?
2. a. Calculer le prix total du bouquet 1.
b. Quelle formule doit‑on écrire dans la feuille de calcul pour calculer ce coût ?
c. Calculer le prix total des quatre bouquets.
3. Donner deux formules de calcul différentes pour calculer le prix total des quatre bouquets.
b. Quelle formule de calcul doit‑on écrire en B6 et étendre vers la droite pour calculer ce total ?
2. a. Calculer le prix total du bouquet 1.
b. Quelle formule doit‑on écrire dans la feuille de calcul pour calculer ce coût ?
c. Calculer le prix total des quatre bouquets.
3. Donner deux formules de calcul différentes pour calculer le prix total des quatre bouquets.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Résoudre des systèmes de deux équations à deux inconnues
1. Résoudre le système suivant par substitution.
\left\{\begin{array}{c}
3 x-y=19 \\
6 x+8 y=8
\end{array}\right.
2. Résoudre le système suivant par combinaison linéaire.
\left\{\begin{array}{l}
7 x-6 y=11 \\
5 x-4 y=4
\end{array}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Modéliser par une mise en équation
À la boulangerie, Aliou achète trois pains au
chocolat et cinq croissants pour 7,10 €.
Assane achète dix pains au chocolat et huit croissants pour 16,30 €.
Déterminer le prix unitaire du croissant et du pain au chocolat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Reconnaître une transformation du plan
Les figures 1 à 5 ont été obtenues par une
transformation du plan, à partir de la figure
originale nommée FIGURE.

Déterminer la nature de chacune de ces transformations planes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Connaître les valeurs remarquables de cosinus et sinus
| x | -\frac{\pi}{2} | \frac{5 \pi}{6} | \frac{\pi}{4} | -\frac{2 \pi}{3} | \pi |
| \cos (x) | |||||
| \sin (x) |
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

