Activités
Histoire des mathématiques
Histoire des mathématiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALes ponts de Königsberg et d'ailleurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En réponse au problème des ponts de Königsberg , Leonhard Euler rédige un article appelé Solutio problematis ad geometriam situs pertinentis, que l'on trouve dans les mémoires de l'Académie des Sciences de Berlin (1759).
Les trois figures ci‑contre en sont extraites.
Cet article a donné naissance à la théorie des graphes.
La figure 1 représente la situation de Königsberg et la figure 3 une situation inventée par Euler pour illustrer le résultat qu'il venait de découvrir. La figure 2 sert à établir une partie de son résultat : si l'itinéraire à suivre contient n ponts à emprunter une et une seule fois, alors il reliera n+1 zones.
Les trois figures ci‑contre en sont extraites.
Cet article a donné naissance à la théorie des graphes.
La figure 1 représente la situation de Königsberg et la figure 3 une situation inventée par Euler pour illustrer le résultat qu'il venait de découvrir. La figure 2 sert à établir une partie de son résultat : si l'itinéraire à suivre contient n ponts à emprunter une et une seule fois, alors il reliera n+1 zones.

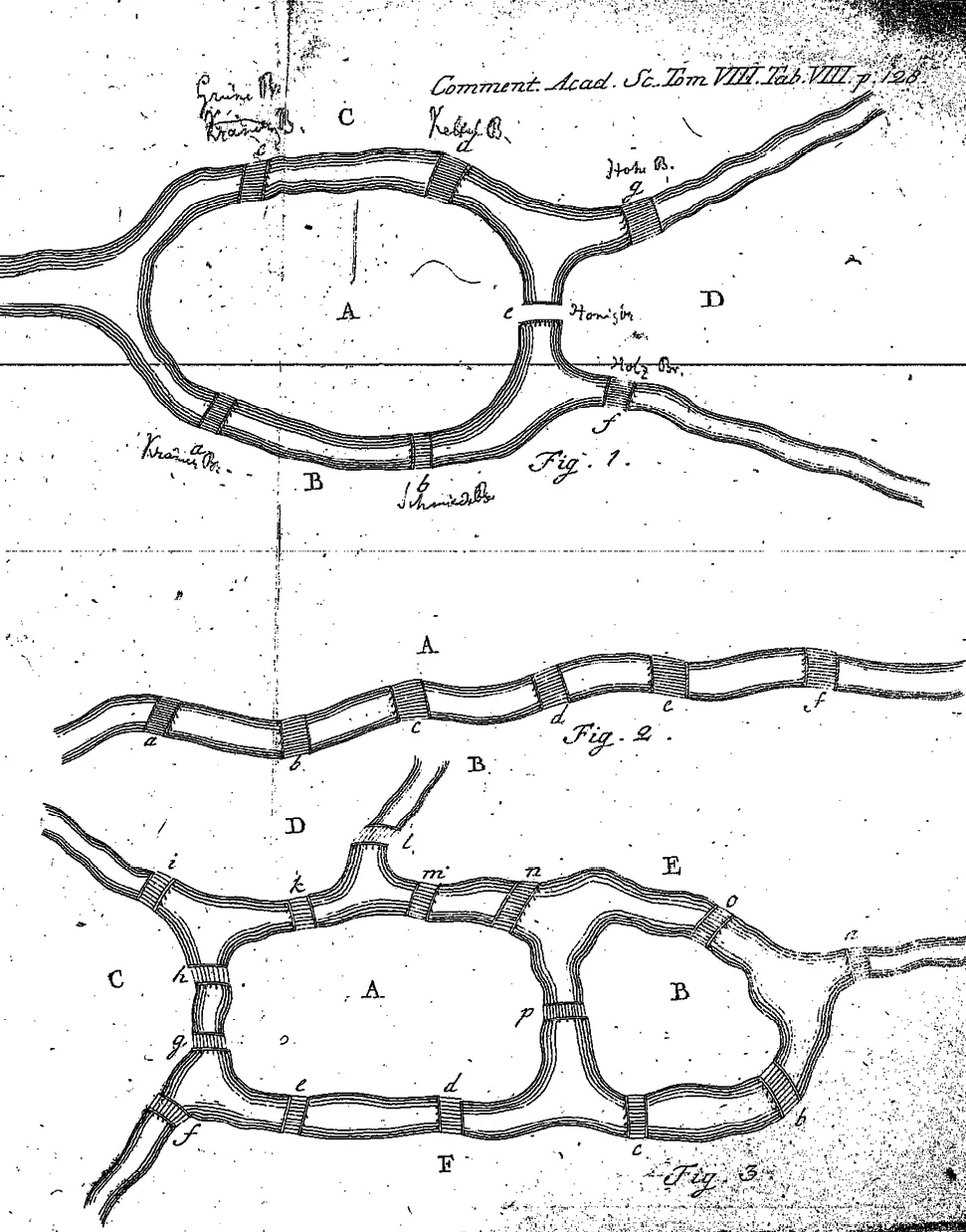
Images tirées de Solutio problematis ad geometriam situs pertinentis de Leonhard Euler.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Tout d'abord, Euler constate que le nombre de ponts qui relient chacune des quatre zones de Königsberg est impair et donc que le problème n'a pas de solution. Expliquer ce raisonnement.Dans la suite de Solutio Problematis ad Geometriam Situs Pertinentis, Euler s'attache à trouver un raisonnement généralisable à toute situation.
2
Dans les paragraphes 11 et 12, Euler montre que si le nombre de ponts qui donnent sur une région A est impair, c'est‑à‑dire qu'il existe un entier naturel p tel que le nombre de ponts soit égal à 2p-1, alors l'itinéraire passe p fois par cette région A.
a) À partir de la figure 1, compléter le tableau ci‑dessous de la situation de Königsberg.
| Zones | A | B | C | D | Somme |
| Nombres de ponts | 5 | 3 | 3 | 3 | |
| \boldsymbol{p} |
b) Expliquer pourquoi le problème des ponts de Königsberg n'a pas de solution.
3
Dans les paragraphes 13 à 15, Euler démontre le résultat général : si le nombre de ponts qui donnent sur une région A est pair, c'est‑à‑dire que s'il existe un entier naturel p tel que le nombre de ponts soit égal à 2p, alors cette région A devra figurer p+1 fois dans l'itinéraire si on part de cette région, ou p fois si on ne fait qu'y passer. Il s'invente la ville représentée en figure 3. En complétant le tableau ci‑dessous, déterminer si on peut suivre ou non un parcours dans cette ville, en empruntant une, et une seule, fois chaque pont.
| Zones | A | B | C | D | E | F | Somme |
| Nombres de ponts | |||||||
| \boldsymbol{p} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BFangcheng et la naissance des matrices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fangcheng, ou Fang Sheng, désigne le nom du 8e chapitre du livre chinois Les Neuf Chapitres sur l'art mathématique, rédigé au début de la période Han entre le IIe siècle avant J.‑C. et le Ier siècle après J.‑C., et qui reprend les savoirs mathématiques chinois connus alors. Fangcheng signifie « comparaison des dispositions ». Les méthodes utilisées dans ce chapitre permettent de résoudre des systèmes de 2 ou 3 équations à 2 ou 3 inconnues, en n'utilisant que des tableaux de nombres qui sont les coefficients de ces équations.


Extrait de Les Neuf Chapitres sur l'art mathématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Premier problème : Deux équations à deux inconnues
3 ballots de riz de bonne qualité et 2 ballots de basse qualité produisent 18 unités de riz, alors que 2 ballots de riz de bonne qualité et 1 de basse qualité produisent 11 unités de riz.
Combien d'unités de riz les ballots de chaque qualité permettent‑ils d'obtenir ?
a) Répondre au problème à l'aide d'un système d'équations.
b) Voici la méthode présentée dans le livre.


Expliquer l'origine du premier tableau de nombres, puis les calculs sur les colonnes pour obtenir le 2e et le 3e tableau. Comment retrouve‑t‑on les solutions obtenues en 1. a) ?
c) En utilisant cette méthode, résoudre le système \left\{\begin{array}{l}6 x+3 y=48 \\ 6 x+5 y=52\end{array}\right..
2
Deuxième problème : Trois équations à trois inconnues
3 ballots de riz de bonne qualité, 2 ballots de qualité moyenne et 1 ballot de basse qualité produisent 39 unités de riz. 2 ballots de riz de bonne qualité, 3 ballots de qualité moyenne et 1 ballot de basse qualité produisent 34 unités de riz. 1 ballot de riz de bonne qualité, 2 ballots de qualité moyenne et 3 ballots de basse qualité produisent 26 unités de riz.
Combien d'unités de riz les ballots de chaque qualité permettent‑ils d'obtenir ?
a) On note respectivement x, y et z le nombre de ballots de riz de bonne, moyenne et basse qualité.
Écrire un système de trois équations à trois inconnues correspondant au problème donné.
b) Voici les étapes de calcul que l'on retrouve dans le livre.

Analyser ces suites de tableaux, compléter les opérations mises en jeu et trouver la solution au problème.
3
En s'inspirant des tableaux ci‑dessus, résoudre le système \left\{\begin{aligned} 3 x+3 y+3 z &=42 \\ x+2 y+4 z &=26 \\ 2 x+4 y+10 z &=57 \end{aligned}\right..Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

