Chapitre 1
Entrée en matière
Nombres entiers
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLe système vicésimal
Il est aujourd'hui naturel pour nous de compter en « base
10 », c'est-à-dire en utilisant dix chiffres (de 0 à 9) pour
construire tous les nombres. Mais cela n'a pas toujours été
le cas. Les Mayas, par exemple, comptaient en base 20 : on
appelle cela le système vicésimal. Ils avaient des symboles
pour représenter les nombres de 0 à 19. C'est aujourd'hui
aussi le cas du peuple des Iñupiat, vivant en Alaska.
D'ailleurs, c'est d'un système vicésimal que vient « quatre- vingts » que l'on utilise encore aujourd'hui. Il s'agit des restes du système utilisé par les Celtes et les Gaulois qui a perduré en France jusqu'au Moyen Âge.
D'ailleurs, c'est d'un système vicésimal que vient « quatre- vingts » que l'on utilise encore aujourd'hui. Il s'agit des restes du système utilisé par les Celtes et les Gaulois qui a perduré en France jusqu'au Moyen Âge.


Le peuple des Iñupiat (Alaska) utilise des chiffres de 0 à 19.
Supplément numérique
Comment écrit-on le nombre 17 avec les chiffres
iñupiaqs ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Le chèque est un moyen
de paiement sur lequel
on doit écrire le montant
payé de deux manières
différentes : en chiffres
dans le cadre à droite et en
toutes lettres sur les lignes
d'écriture.
En cas d'erreur, si les deux montants sont différents, c'est celui écrit en toutes lettres qui sera considéré comme le montant à verser au bénéficiaire.
En cas d'erreur, si les deux montants sont différents, c'est celui écrit en toutes lettres qui sera considéré comme le montant à verser au bénéficiaire.


Que doit-on écrire sur les lignes afin que ce chèque soit
correctement rempli ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Numération égyptienne
En Égypte antique, les scribes égyptiens écrivaient les
nombres entiers à l'aide des symboles ci-dessous.

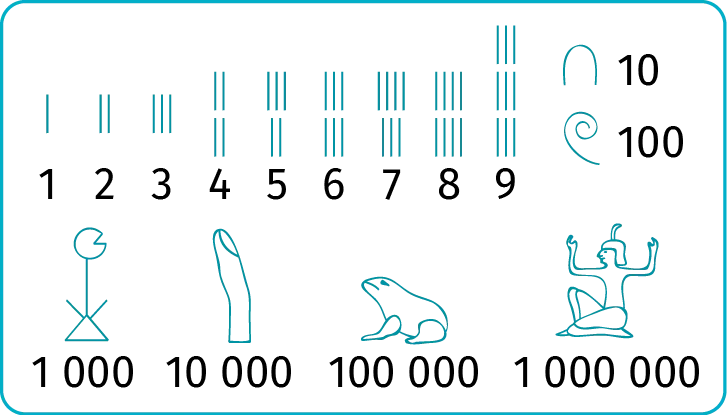


1. Quel nombre est représenté par l'image ci-dessous ?

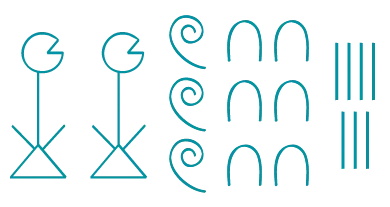 2. Comment représente-t-on le nombre 267 ? 405 ? 1 213 ? 46 458 ?
2. Comment représente-t-on le nombre 267 ? 405 ? 1 213 ? 46 458 ?

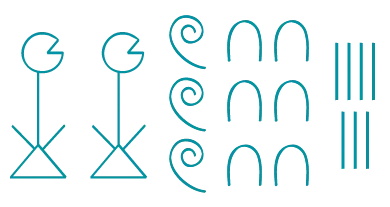
Cliquez ici pour avoir accès à un espace de dessin
Bilan
Quels sont les inconvénients du système de numération égyptien ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2 Passer du million au milliard
Un million est égal à mille milliers et un milliard est égal à mille millions.
1. Combien de millions représentent 3 milliards ? 40 milliards ? 178 milliards ?
2.
a. Comment lire le nombre 14 520 940 063 ?
b. Quel est son chiffre des dizaines de milliards ? Et son nombre de milliards ?
Recopier et compléter le tableau suivant en précisant ce que signifient les lettres C, D et U.
1. Combien de millions représentent 3 milliards ? 40 milliards ? 178 milliards ?
Bilan
Recopier et compléter le tableau suivant en précisant ce que signifient les lettres C, D et U.
| Millions | Milliers | Unités | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | D | U | C | D | U | C | D | U | |||
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationManipuler un abaque
Pour réaliser cette activité, utiliser
Par combien doit-on multiplier pour passer d'un million à un milliard ?
1.
Représenter le nombre 137 542 sur l'abaque. Pour ajouter 48 à ce nombre, on ajoute quatre
jetons sur le pic des dizaines et huit jetons sur le pic des unités. Que remarque-t-on ?
2. Lorsqu'un pic contient dix jetons, on les enlève de ce pic et on en ajoute un sur le pic à
sa gauche. Quel nombre est alors représenté ? Quel chiffre indique le pic de droite ?
3. Ajouter cinq jetons sur le pic des milliers, deux jetons sur le pic des centaines, quatre
sur le pic des dizaines et huit sur celui des unités. Quel nombre ajoute-t-on ? Quel est le
nombre obtenu ?
4. Décaler tous les jetons d'un pic vers la gauche : quel est alors le nombre représenté ? Par
combien a-t-on multiplié le nombre de départ ?
5. Décaler tous les jetons de trois pics vers la gauche : par combien a-t-on multiplié ?
6. Représenter le nombre 154 036, ajouter 563 928 puis multiplier par 1 000, qu'obtient-on ?
Bilan
Par combien doit-on multiplier pour passer d'un million à un milliard ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


