Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 1
Cours
Nombres entiers
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Écrire les nombres entiers
Définition
Pour écrire un nombre entier dans notre système décimal, on utilise les dix chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
- Remarque : Pour faciliter la lecture des grands nombres, on regroupe les chiffres par trois à partir de la droite : le nombre 1544138652 s'écrit 1 544 138 652.
Définition
Un milliard est égal à mille millions. On peut alors écrire 1 000 000 000 = 1 000 × 1 000 000.
- Remarque : Dans le tableau de position, la colonne des unités de milliards se situe trois colonnes à gauche de celle des unités de millions.
Exemple :
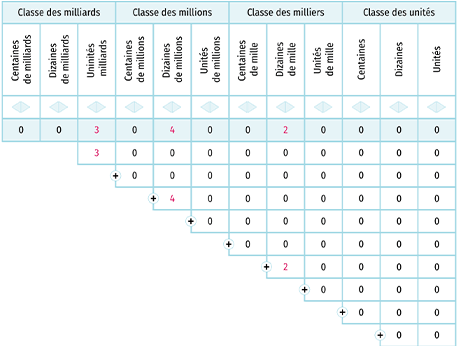
Dans le nombre 3 {\color{red}6}54 927 {\color{blue}6}14, le {\color{red}6} en rouge représente la quantité 600 000 000, alors que le {\color{blue}6} en bleu représente la quantité 600 :
3 654 927 614 = 365 × 10 000 000 + 4 927 614.
| Classe des milliards | Classe des millions | Classe des milliers | Classe des unités | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Centaines de milliards | Dizaines de milliards | Unités de milliards | Centaines de millions | Dizaines de millions | Unités de millions | Centaines de mille | Dizaines de mille | Unités de mille | Centaines | Dizaines | Unités |
| 3 | {\color{red}6} | 5 | 4 | 9 | 2 | 7 | {\color{blue}6} | 1 | 4 | ||
Dans le nombre 3 {\color{red}6}54 927 {\color{blue}6}14, le {\color{red}6} en rouge représente la quantité 600 000 000, alors que le {\color{blue}6} en bleu représente la quantité 600 :
\begin{aligned}
& 3~{\color{red}6}54~927~{\color{blue}6}14=3 \times 1~000~000~000+{\color{red}6} \times 100~000~000+5 \times 10~000~000 + \\
& 4 \times 1~000~000+9 \times 100~000+2 \times 10~000+7 \times 1~000+{\color{blue}6} \times 100+1 \times 10+4 \times 1 .
\end{aligned}
Dans ce nombre, le chiffre des dizaines de millions est 5 mais le nombre de dizaines de
millions est 365, en effet on peut écrire3 654 927 614 = 365 × 10 000 000 + 4 927 614.
Règles d'orthographe pour l'écriture des nombres en lettres
- Si un nombre s'écrit en plusieurs mots, on met un trait d'union entre chaque mot.
- Les mots « vingt » et « cent » se terminent par un « s » s'ils sont le dernier mot du nombre et qu'ils sont multipliés (six-cents, quatre-vingts, mais six-cent-dix et quatre-vingt-cinq).
- Le mot « mille » est invariable, il ne prend jamais de « s ».
- Les mots « million » et « milliard » s'accordent au pluriel.
Exemple :
13 127 806 280 s'écrit « treize-milliards-cent-vingt-sept-millions-huit-cent-six-mille-deux-cent-quatre-vingts ».
13 127 806 280 s'écrit « treize-milliards-cent-vingt-sept-millions-huit-cent-six-mille-deux-cent-quatre-vingts ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Comparer les nombres entiers
Définition
Comparer deux nombres, c'est dire lequel est le plus grand, lequel est le plus petit, ou s'ils sont égaux. Ranger des nombres dans l'ordre croissant, c'est les ordonner du plus petit au plus grand. Les ranger dans l'ordre décroissant, c'est les ordonner du plus grand au plus petit.
Notation
Pour comparer deux nombres, on utilise les symboles suivants.
- Égalité : le symbole = signifie « est égal à ».
- Inégalités strictes : le symbole < signifie « est strictement inférieur à » et le symbole > signifie « est strictement supérieur à »
- Inégalités larges : le symbole ≤ signifie « est inférieur ou égal à » et le symbole ≥ signifie « est supérieur ou égal à »
Exemples :
1. Le nombre 12 est strictement inférieur au nombre 15 donc on note 12 < 15.
2. Les nombres suivants sont rangés dans l'ordre décroissant : 200 >94 >47 >26 >9 >2.
3. Si on choisit un nombre n compris entre 0 et 10, on peut décider d'inclure 0 et 10. On écrit alors 0 ≤ n ≤ 10. Si on décide d'exclure 0 et 10, on écrit 0 < n < 10 (on dit que n est strictement compris entre 0 et 10).
4. Choisir un nombre x tel que 6 ≤ x < 15 signifie qu'on peut choisir n'importe quel nombre entre 6 inclus et 15 exclu.
1. Le nombre 12 est strictement inférieur au nombre 15 donc on note 12 < 15.
2. Les nombres suivants sont rangés dans l'ordre décroissant : 200 >94 >47 >26 >9 >2.
3. Si on choisit un nombre n compris entre 0 et 10, on peut décider d'inclure 0 et 10. On écrit alors 0 ≤ n ≤ 10. Si on décide d'exclure 0 et 10, on écrit 0 < n < 10 (on dit que n est strictement compris entre 0 et 10).
4. Choisir un nombre x tel que 6 ≤ x < 15 signifie qu'on peut choisir n'importe quel nombre entre 6 inclus et 15 exclu.
- Remarque : Si deux nombres entiers n'ont pas le même nombre de chiffres, celui qui en a le plus est le plus grand. S'ils ont le même nombre de chiffres, on compare leurs chiffres un à un de gauche à droite jusqu'à en trouver un qui diffère pour permettre la comparaison.
Définition
Encadrer un nombre, c'est donner un nombre plus petit et un nombre plus grand que le nombre en question. Encadrer un nombre à la dizaine près, c'est encadrer ce nombre par les deux dizaines les plus proches. De la même manière, l'encadrer à la centaine près revient à encadrer par les deux centaines les plus proches, et ainsi de suite.
Exemples :
1. Puisque 7 129 452 321 < 8 200 453 234 < 9 000 000 000, alors on peut encadrer 8 200 453 234 avec les nombres 7 129 452 321 et 9 000 000 000.
2. Puisque 8 224 453 200 < 8 224 453 234 < 8 224 453 300, on peut également encadrer 8 224 453 234 avec les nombres 8 224 453 200 et 8 224 453 300 : il s'agit ici d'un encadrement à la centaine.
1. Puisque 7 129 452 321 < 8 200 453 234 < 9 000 000 000, alors on peut encadrer 8 200 453 234 avec les nombres 7 129 452 321 et 9 000 000 000.
2. Puisque 8 224 453 200 < 8 224 453 234 < 8 224 453 300, on peut également encadrer 8 224 453 234 avec les nombres 8 224 453 200 et 8 224 453 300 : il s'agit ici d'un encadrement à la centaine.
Définition
Un ordre de grandeur d'un nombre est une valeur proche de ce nombre.
Exemple :
Un ordre de grandeur de 124 652 954 321 au million près est 124 653 000 000.
Un ordre de grandeur de 124 652 954 321 au million près est 124 653 000 000.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
