Mathématiques 6e - 2025
Mes Pages
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 2
Cours
Notion de fraction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Sens quotient d'une fraction
Définitions
Pour tout entier b ≠ 0, la fraction \frac{1}{b} correspond à une part de l'unité lors du partage de cette unité en b parts égales.
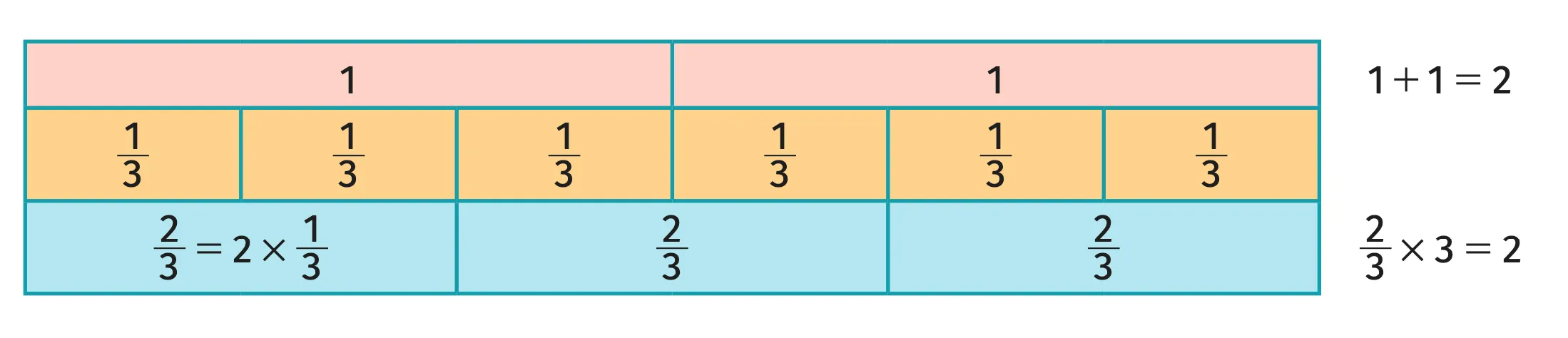
Pour tout entier a, on note \frac{a}{b}=\underbrace{\frac{1}{b}+\frac{1}{b}+\ldots+\frac{1}{b}}_{a \text { fois }}=a \times \frac{1}{b}.
Le nombre a est appelé le numérateur de la fraction et le nombre b est le dénominateur.
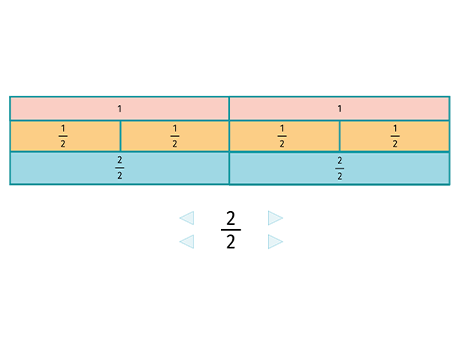
- Remarque : Si b ≠ 0, on voit donc que b \times \frac{1}{b} = \frac{b}{b} = 1
Propriété
La fraction \frac{a}{b}, avec b ≠ 0, est le nombre qui, multiplié par b, donne a : \frac{a}{b} \times b = b \times \frac{a}{b} = a.
- Remarque : On peut justifier cette propriété avec la calcul suivant : b \times \frac{a}{b} = b \times a \times \frac{1}{b} = a \times b \times \frac{1}{b} = a \times 1 = a.
Exemple :
La fraction \frac{2}{3} est le nombre qui, multiplié par 3, donne 2 ; c'est-à-dire \frac{2}{3} \times 3 = 3 \times \frac{2}{3} = 2.
La fraction \frac{2}{3} est le nombre qui, multiplié par 3, donne 2 ; c'est-à-dire \frac{2}{3} \times 3 = 3 \times \frac{2}{3} = 2.
Propriété
Pour deux nombres entiers a et b avec b ≠ 0, la fraction \frac{a}{b} est le résultat exact de la division de a par b. C'est le quotient de a par b, autrement dit,
\frac{a}{b} = a \div b.
Exemple :
\frac{9}{4} = 2,25 car 9 \div 4 = 2,25.
\frac{9}{4} = 2,25 car 9 \div 4 = 2,25.
Définition
Pour tout nombre a, le nombre \frac{a}{100} est appelé pourcentage. On peut aussi l'écrire a \%.
Exemple :
50 \% est une autre écriture de la fraction \frac{50}{100}, mais aussi de la fraction \frac{1}{2}, ou encore du nombre 0,5. Autrement dit, 50 \% = \frac{50}{100} = 0,5 = \frac{1}{2}.
50 \% est une autre écriture de la fraction \frac{50}{100}, mais aussi de la fraction \frac{1}{2}, ou encore du nombre 0,5. Autrement dit, 50 \% = \frac{50}{100} = 0,5 = \frac{1}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Comparaisons de fractions
Propriété
Le nombre représenté par une fraction ne change pas lorsque l'on multiplie ou lorsque l'on divise le numérateur et le dénominateur de celle-ci par un même nombre non nul.
Exemples :
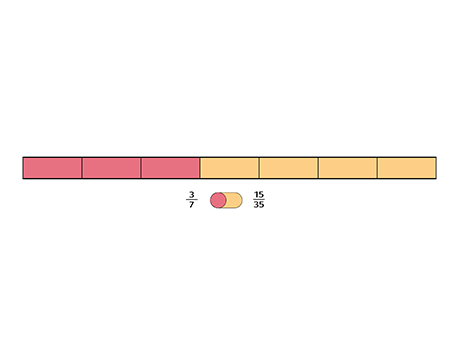
1. \frac{3}{7}=\frac{3 {\color{red} \times 5}}{7 {\color{red}\times 5}}=\frac{15}{35}
2. \frac{24}{16}=\frac{24 {\color{red}\div8}}{16 {\color{red}\div 8}}=\frac{3}{2}. Ici, on obtient une fraction simplifiée avec un numérateur et un dénominateur plus petits que ceux de la fraction initiale.
3. On peut aussi simplifier une fraction avec des décompositions : \frac{15}{10}=\frac{3 {\color{red}\times5}}{2 {\color{red}\times 5}}=\frac{3}{2}.
1. \frac{3}{7}=\frac{3 {\color{red} \times 5}}{7 {\color{red}\times 5}}=\frac{15}{35}
2. \frac{24}{16}=\frac{24 {\color{red}\div8}}{16 {\color{red}\div 8}}=\frac{3}{2}. Ici, on obtient une fraction simplifiée avec un numérateur et un dénominateur plus petits que ceux de la fraction initiale.
3. On peut aussi simplifier une fraction avec des décompositions : \frac{15}{10}=\frac{3 {\color{red}\times5}}{2 {\color{red}\times 5}}=\frac{3}{2}.
Propriétés
1. Si deux fractions ont le même dénominateur, alors la fraction avec le plus grand numérateur est la fraction la plus grande.
2. Si deux fractions ont le même numérateur, alors la fraction avec le plus grand dénominateur est la fraction la plus petite.
Exemples :
1. \frac{5}{8} et \frac{3}{8} ont le même dénominateur. On a 5 > 3 donc \frac{5}{8} > \frac{3}{8}. En effet, la fraction \frac{5}{8} représente 5 fois \frac{1}{8} alors que la fraction \frac{3}{8} ne représente que 3 fois \frac{1}{8}.
2. \frac{8}{15} et \frac{8}{10} ont le même numérateur. On a 15 > 10 donc \frac{8}{15} < \frac{8}{10}.
1. \frac{5}{8} et \frac{3}{8} ont le même dénominateur. On a 5 > 3 donc \frac{5}{8} > \frac{3}{8}. En effet, la fraction \frac{5}{8} représente 5 fois \frac{1}{8} alors que la fraction \frac{3}{8} ne représente que 3 fois \frac{1}{8}.
2. \frac{8}{15} et \frac{8}{10} ont le même numérateur. On a 15 > 10 donc \frac{8}{15} < \frac{8}{10}.
Propriétés
1. Une fraction est égale à 1 si et seulement si son numérateur est égal à son dénominateur.
2. Une fraction est strictement inférieure à 1 si et seulement si son numérateur est strictement inférieur à son dénominateur.
3. Une fraction est strictement supérieure à 1 si et seulement si son numérateur est strictement supérieur à son dénominateur.
Exemples :
1. \frac{5}{8} < 1 car 5 < 8.
2. \frac{7}{4} > 1 car 7 > 4.
3. \frac{3761}{3761} = 1 car le numérateur et le dénominateur sont égaux.
1. \frac{5}{8} < 1 car 5 < 8.
2. \frac{7}{4} > 1 car 7 > 4.
3. \frac{3761}{3761} = 1 car le numérateur et le dénominateur sont égaux.
- Remarque : En utilisant la comparaison d'une fraction avec 1, on peut comparer deux fractions de dénominateurs différents dans certains cas.
Exemple :
On souhaite comparer \frac{5}{4} et \frac{3}{7}.
D'une part, on sait \frac{5}{4} > 1 car 5 > 4. D'autre part, \frac{3}{7} < 1. On en déduit que \frac{5}{4} > \frac{3}{7}.
On souhaite comparer \frac{5}{4} et \frac{3}{7}.
D'une part, on sait \frac{5}{4} > 1 car 5 > 4. D'autre part, \frac{3}{7} < 1. On en déduit que \frac{5}{4} > \frac{3}{7}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
