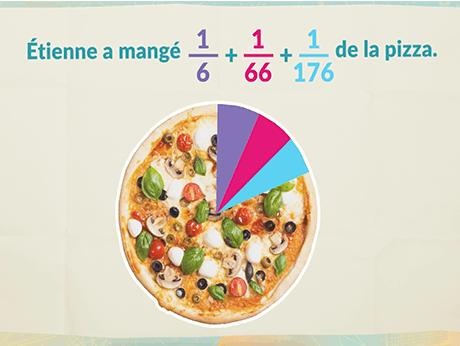Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 3
Entrée en matière
Opérations sur les fractions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLes sommes de fractions unitaires
Comme cela a été vu dans le chapitre 2 , en Égypte antique, on utilisait
uniquement des fractions unitaires en plaçant un symbole en forme de bouche au-dessus d'un nombre qui représentait le dénominateur.
Cependant, on a retrouvé des problèmes datant de cette période et faisant appel à des fractions non unitaires dans le papyrus de Rhind. Alors, comment cela est-il possible ?
Les savants et savantes de l'époque utilisaient des décompositions de fractions en fractions unitaires avec des dénominateurs différents.
Par exemple, \frac{2}{5}=\frac{1}{3}+\frac{1}{15}. En effet, \frac{1}{3}+\frac{1}{15}=\frac{1 \times 5}{3 \times 5} +\frac{1}{15}=\frac{5}{15}+\frac{1}{15}=\frac{6}{15}=\frac{6÷3}{15÷3}=\frac{2}{5}.
On a alors une fraction non unitaire écrite comme somme de fractions unitaires. Il est possible d'écrire n'importe quelle fraction inférieure à 1 sous la forme de fractions unitaires et donc de l'écrire avec les hiéroglyphes égyptiens.
Cependant, on a retrouvé des problèmes datant de cette période et faisant appel à des fractions non unitaires dans le papyrus de Rhind. Alors, comment cela est-il possible ?
Les savants et savantes de l'époque utilisaient des décompositions de fractions en fractions unitaires avec des dénominateurs différents.
Par exemple, \frac{2}{5}=\frac{1}{3}+\frac{1}{15}. En effet, \frac{1}{3}+\frac{1}{15}=\frac{1 \times 5}{3 \times 5} +\frac{1}{15}=\frac{5}{15}+\frac{1}{15}=\frac{6}{15}=\frac{6÷3}{15÷3}=\frac{2}{5}.
On a alors une fraction non unitaire écrite comme somme de fractions unitaires. Il est possible d'écrire n'importe quelle fraction inférieure à 1 sous la forme de fractions unitaires et donc de l'écrire avec les hiéroglyphes égyptiens.
Justifier que \frac{3}{5} = \frac{1}{2} + \frac{1}{10}.
Supplément numérique
Retrouvez cette histoire en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Les fractions font partie de notre quotidien sans que nous nous en
rendions nécessairement compte. Que signifie la phrase « J'arrive
dans un quart d'heure » ? Cela veut dire que l'on divise l'heure en 4,
ou encore que l'on divise 60 \text{~min} en 4, soit 60 \text{~min} ÷ 4 = 15 \text{~min}. Ainsi,
un quart d'heure représente 15 minutes. De la même façon, lorsque
l'on dit qu'un film dure une heure et demie, cela représente
1 \text{~h} + \frac{1}{2} \text{~h}.
Combien y a-t-il de quarts d'heure dans \frac{3}{4} \text{~h} ? Combien de minutes cela représente-t-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Comprendre l'addition de fractions
On considère les gâteaux suivants partagés de la même façon en parts égales.
Les parts colorées sont celles qui ont été mangées.
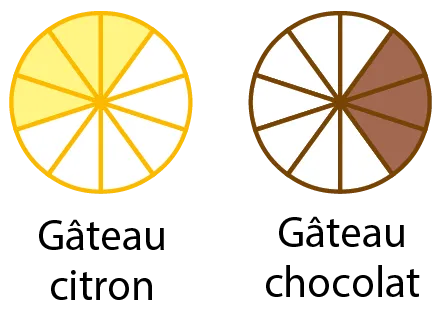
1. a. Quelle fraction du gâteau au citron a été mangée ?
b. Quelle fraction du gâteau au chocolat a été mangée ?
c. En prenant comme unité un gâteau entier, quelle fraction totale
de gâteaux (citron et chocolat) a été mangée ?
d. Recopier et compléter : \frac{4}{10} + \frac{3}{10} = \frac{\ldots}{10}.
1. a. Quelle fraction du gâteau au citron a été mangée ?
On considère maintenant les gâteaux ci-dessous. L'unité est toujours un gâteau entier.
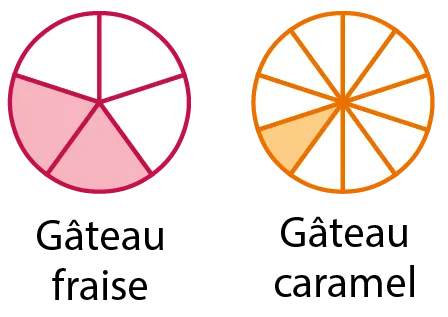
2. a. Exprimer avec une somme de deux fractions la quantité de gâteau mangée.
b. Peut-on calculer cette somme comme précédemment ? Justifier.
c. Recopier ces schémas de gâteaux en découpant autrement celui
à la fraise pour savoir quelle fraction totale de gâteau a été mangée.
Expliquer une méthode pour additionner deux fractions.
2. a. Exprimer avec une somme de deux fractions la quantité de gâteau mangée.
Cliquez ici pour avoir accès à un espace de dessin
Bilan
Expliquer une méthode pour additionner deux fractions.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationCalculer une fraction d'une quantité
Pour réaliser cette activité, utiliser la .
Emma a mangé \frac{3}{4} de sa tablette de chocolat composée de vingt carrés de chocolat. On cherche combien de carrés elle a mangés. L'unité est la tablette de chocolat complète.
1. a. Partager la tablette nº1 en quatre parts égales. Quelle fraction de la tablette représente une part ? Combien y a-t-il de carrés dans une part ? Quelle division permet de trouver cette valeur ?
b. Hachurer en bleu trois de ces parts. Quelle fraction de la
tablette représentent ces trois parts ? Combien de carrés sont alors
hachurés ? Quelle multiplication permet de trouver cette valeur ?
c. Recopier et compléter la phrase suivante avec les symboles \times et \div.
« Pour calculer \frac{3}{4} de 20, on peut effectuer le calcul (20 \ldots 4) \ldots 3. »
2. Recopier et compléter la phrase suivante.
« \frac{3}{4} de la tablette de 20 carrés c'est ... fois le quart de la tablette de vingt carrés, c'est-à-
dire \frac{20}{4} + \frac{20}{4} + \frac{20}{4} = \frac{20 \times \ldots}{4} »
En utilisant chacune des questions précédentes, recopier et compléter la phrase suivante.
« Pour calculer \frac{3}{4} de 20, on peut effectuer le calcul (20 \ldots 4) \ldots 3 ou (20 \ldots 3) \ldots 4. Sous forme fractionnaire, cela donne \frac{3}{4} \ldots 20 ou encore 20 \ldots \frac{3}{4}. »
Emma a mangé \frac{3}{4} de sa tablette de chocolat composée de vingt carrés de chocolat. On cherche combien de carrés elle a mangés. L'unité est la tablette de chocolat complète.
1. a. Partager la tablette nº1 en quatre parts égales. Quelle fraction de la tablette représente une part ? Combien y a-t-il de carrés dans une part ? Quelle division permet de trouver cette valeur ?
Bilan
En utilisant chacune des questions précédentes, recopier et compléter la phrase suivante.
« Pour calculer \frac{3}{4} de 20, on peut effectuer le calcul (20 \ldots 4) \ldots 3 ou (20 \ldots 3) \ldots 4. Sous forme fractionnaire, cela donne \frac{3}{4} \ldots 20 ou encore 20 \ldots \frac{3}{4}. »
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
