Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Chapitre 3
Cours
Opérations sur les fractions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Addition et soustraction de fractions
Propriété
Pour additionner ou soustraire des fractions de même dénominateur non nul, on ajoute ou soustrait les numérateurs et on conserve le même dénominateur.
Méthode
Pour additionner ou soustraire des fractions de dénominateurs différents, on les exprime d'abord avec le même dénominateur, puis on applique la propriété précédente.
Exemples :
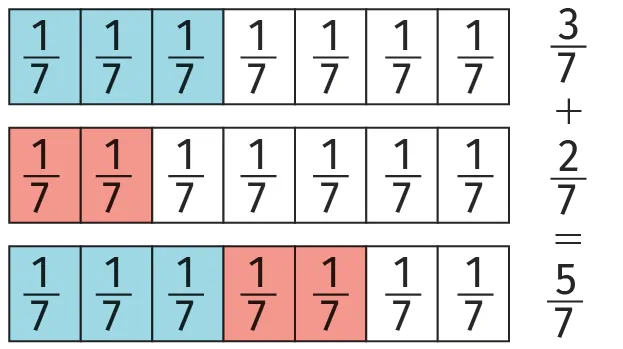
1. \frac{3}{7} + \frac{2}{7} = \frac{3+2}{7} = \frac{5}{7}
2. \frac{8}{5} - \frac{6}{5} = \frac{8-6}{5} = \frac{2}{5}
3. \frac{5}{3} + \frac{7}{6} = \frac{5 \times 2}{3 \times 2} + \frac{7}{6} = \frac{10}{6} + \frac{7}{6} = \frac{10+7}{6} = \frac{17}{6}
2. \frac{8}{5} - \frac{6}{5} = \frac{8-6}{5} = \frac{2}{5}
3. \frac{5}{3} + \frac{7}{6} = \frac{5 \times 2}{3 \times 2} + \frac{7}{6} = \frac{10}{6} + \frac{7}{6} = \frac{10+7}{6} = \frac{17}{6}
- Remarque :
On dit que l'on réduit deux fractions au même dénominateur lorsqu'on les écrit avec un dénominateur commun.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Nombre mixte, encadrement et comparaison
Propriété
Toute fraction peut se décomposer de façon unique comme la somme d'un nombre entier et d'une fraction strictement inférieure à 1. La fraction est alors écrite sous la forme d'un nombre mixte.
Exemples :
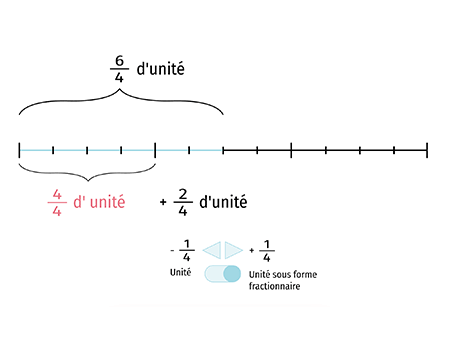
1. \frac{5}{4}=\frac{4}{4}+\frac{1}{4}=1+\frac{1}{4}
2. \frac{17}{5}=\frac{5}{5}+\frac{5}{5}+\frac{5}{5}+\frac{2}{5}=1+1+1+\frac{2}{5}=3+\frac{2}{5}
3. \frac{26}{6}=\frac{24+2}{6}=\frac{24}{6}+\frac{2}{6}=4+\frac{2}{6}
4. \frac{1}{4} : l'écriture sous forme d'un nombre mixte d'une fraction inférieur à 1 est elle-même.
2. \frac{17}{5}=\frac{5}{5}+\frac{5}{5}+\frac{5}{5}+\frac{2}{5}=1+1+1+\frac{2}{5}=3+\frac{2}{5}
3. \frac{26}{6}=\frac{24+2}{6}=\frac{24}{6}+\frac{2}{6}=4+\frac{2}{6}
4. \frac{1}{4} : l'écriture sous forme d'un nombre mixte d'une fraction inférieur à 1 est elle-même.
- Remarque :
Cette propriété facilite l'encadrement des fractions entre deux entiers consécutifs. On peut aussi l'utiliser pour comparer des fractions qui n'ont pas le même dénominateur.
Exemple :
• On veut encadrer \frac{12}{5} et \frac{13}{3} par deux entiers consécutifs.
\frac{12}{5}=\frac{10}{5}+\frac{2}{5}=2+\frac{2}{5}. Comme 2 <2+\frac{2}{5}<3, on en déduit que 2<\frac{12}{5} <3.
\frac{13}{3}=\frac{12}{3}+\frac{1}{3}=4+\frac{1}{3}. Comme 4 <4+\frac{1}{3}<5, on en déduit que 4<\frac{13}{3}<5.
• On veut maintenant comparer \frac{12}{5} et \frac{13}{3}.
D'après le premier point, on sait que 2<\frac{12}{5}<3 et que 4<\frac{13}{3}<5 donc \frac{12}{5}<\frac{13}{3}.
• On veut encadrer \frac{12}{5} et \frac{13}{3} par deux entiers consécutifs.
\frac{12}{5}=\frac{10}{5}+\frac{2}{5}=2+\frac{2}{5}. Comme 2 <2+\frac{2}{5}<3, on en déduit que 2<\frac{12}{5} <3.
\frac{13}{3}=\frac{12}{3}+\frac{1}{3}=4+\frac{1}{3}. Comme 4 <4+\frac{1}{3}<5, on en déduit que 4<\frac{13}{3}<5.
• On veut maintenant comparer \frac{12}{5} et \frac{13}{3}.
D'après le premier point, on sait que 2<\frac{12}{5}<3 et que 4<\frac{13}{3}<5 donc \frac{12}{5}<\frac{13}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Fraction d'un nombre
Propriété
Pour calculer une fraction d'un nombre, on multiplie cette fraction par ce nombre.
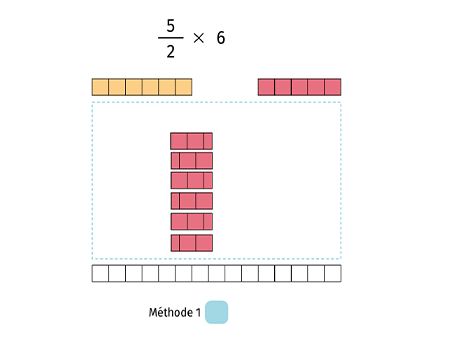
Méthode 1
Calculer \frac{5}{2} de 6 revient à calculer \frac{5}{2} \times 6.
Dans ce cas, on peut d'abord effectuer la division de 5 par 2, puis multiplier par 6.
On a ainsi \frac{5}{2} \times 6 = (5 \div 2) \times 6 = 2,5 \times 6 = 15.
Méthode 2
On peut aussi interpréter \frac{5}{2} de 6 comme 5 fois la moitié de 6, c'est-à-dire 5 \times \frac{6}{2}.
Dans ce cas, on peut d'abord effectuer la division de 6 par 2, puis multiplier par 5.
On a ainsi \frac{5}{2} \times 6 = 5 \times (6 \div 2) = 5 \times 3 = 15.
Méthode 3
On peut également voir \frac{5}{2} \times 6 comme \frac{5}{2} + \frac{5}{2} + \frac{5}{2} + \frac{5}{2} + \frac{5}{2} + \frac{5}{2} = \frac{5+5+5+5+5+5}{2} = \frac{5 \times 6}{2}.
Dans ce cas, on effectue d'abord le produit de 5 par 6, puis on divise par 2.
On a ainsi \frac{5}{2} \times 6 = (5 \times 6) \div 2 = 30 \div 2 = 15.
- Remarque :
Ces trois méthodes donnent le même résultat. Le choix de la méthode ne changera donc pas le résultat sauf si les nombres obtenus dans les calculs intermédiaires sont arrondis. On choisit donc la méthode la plus adaptée à la situation. - Conséquence : Calculer a \% d'un nombre revient à multiplier ce nombre par \frac{a}{100}.
Exemple :
Calculer 20 \% de 50 revient à calculer \frac{20}{100} \times 50 soit \frac{20 \times 50}{100} = \frac{1 000}{100} = 10.
Donc 20 \% de 50 sont égaux à 10.
Calculer 20 \% de 50 revient à calculer \frac{20}{100} \times 50 soit \frac{20 \times 50}{100} = \frac{1 000}{100} = 10.
Donc 20 \% de 50 sont égaux à 10.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
