Chapitre 12
Entraînement
Droites et segments
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Premiers éléments de géométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
À l'oral
Deux demi-droites forment-elles toujours une droite ? Justifier la réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
À l'oral
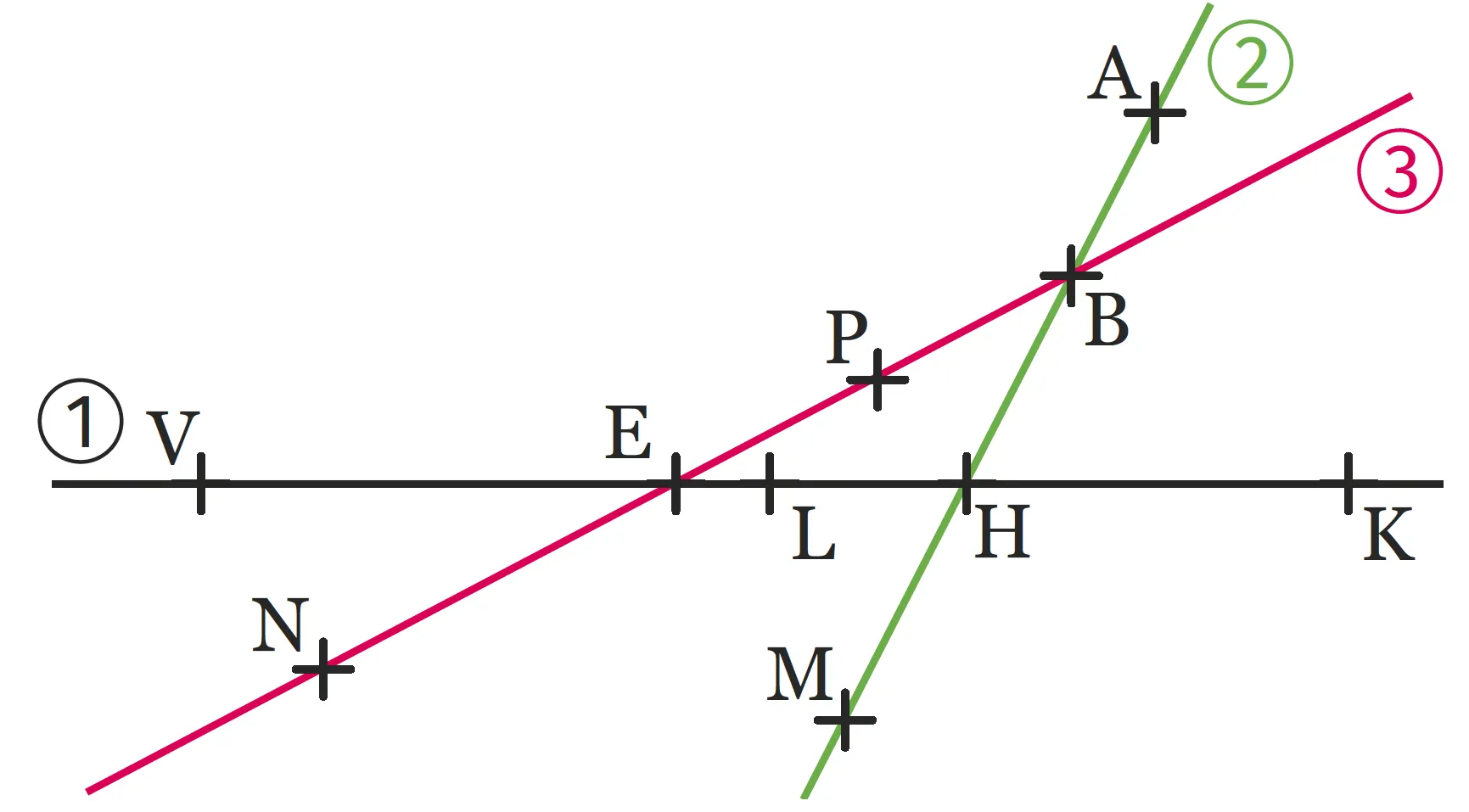
En utilisant les noms des points de
la figure ci-dessous, lister différentes
façons de nommer la droite noire 1,
la verte 2 et la rouge 3.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
À l'oral
Traduire par des mots chacune des
notations suivantes.
1. \text {(NM)}
2. \text {[EK)}
3. \text {[NB)}
4. (d)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
À l'oral
Traduire par une phrase chacune
des notations suivantes.
1. \mathrm{M} \in(d)
2. \mathrm{P} \in [\mathrm{AB})
3. \mathrm{L} \notin(\mathrm{CD})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Sur une droite, placer trois points
distincts \mathrm{H}, \mathrm{D} et \mathrm{F}. Nommer cette droite
de trois manières différentes.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Réaliser la construction suivante.
1. Tracer une droite \mathrm{(PG)}.
2. Placer un point \mathrm{R} tel que \mathrm{R ∉ (PG)}.
3. Tracer la demi-droite [\mathrm{PR}) en rouge.
4. Tracer la demi-droite [\mathrm{RG}) en vert.
1. Tracer une droite \mathrm{(PG)}.
2. Placer un point \mathrm{R} tel que \mathrm{R ∉ (PG)}.
3. Tracer la demi-droite [\mathrm{PR}) en rouge.
4. Tracer la demi-droite [\mathrm{RG}) en vert.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
1.
a. Tracer une droite \left(d_1\right).
b. Placer deux points \mathrm{A} et \mathrm{B} qui appartiennent à cette droite.
2. Placer un point \mathrm{M} tel que \mathrm{M} \in[\mathrm{AB}].
3.
a. Tracer une droite \left(d_2\right) passant par \mathrm{M} et ne passant pas par \mathrm{A}.
b. La droite \left(d_2\right) peut-elle passer par le
point \mathrm{B} ? Justifier.
a. Tracer une droite \left(d_1\right).
b. Placer deux points \mathrm{A} et \mathrm{B} qui appartiennent à cette droite.
2. Placer un point \mathrm{M} tel que \mathrm{M} \in[\mathrm{AB}].
3.
a. Tracer une droite \left(d_2\right) passant par \mathrm{M} et ne passant pas par \mathrm{A}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Réaliser la construction suivante.
1. Placer deux points distincts \mathrm{T} et \mathrm{U}.
2. Tracer en noir la droite \mathrm{(TU)}.
3. Placer un point \mathrm{R} n'appartenant pas à la droite \mathrm{(TU)}.
4. Tracer en vert la demi-droite \text {[RU)}.
5. Tracer en bleu la demi-droite \text {[TR)}.
1. Placer deux points distincts \mathrm{T} et \mathrm{U}.
2. Tracer en noir la droite \mathrm{(TU)}.
3. Placer un point \mathrm{R} n'appartenant pas à la droite \mathrm{(TU)}.
4. Tracer en vert la demi-droite \text {[RU)}.
5. Tracer en bleu la demi-droite \text {[TR)}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Traduire par une phrase chacune des
notations suivantes.
1. \mathrm{[NA)}
2. \mathrm{B∈[AT)}
3. \mathrm{N∉(AC)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
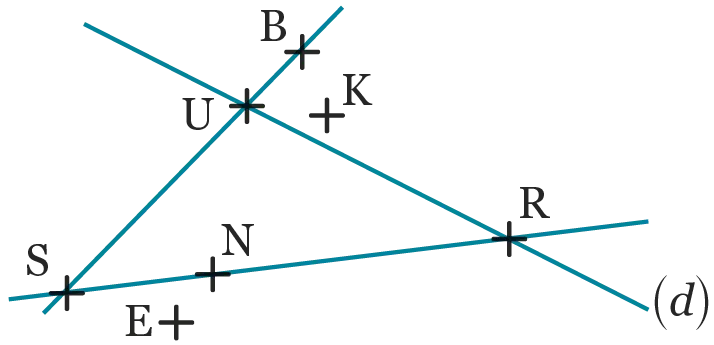
Pour les exercices 28 à 30, à l'aide de la figure suivante, compléter les propositions avec \mathrm{∈} ou \mathrm{∉}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
1. \mathrm{S} \text {(NR)}
2. \mathrm{E} \text {(UR)}
3. \mathrm{U} (d)
2. \mathrm{E} \text {(UR)}
3. \mathrm{U} (d)
4. \mathrm{U} \text {(RB)}
5. \mathrm{N} \text {(KE)}
6. \mathrm{B} \text {(US)}
5. \mathrm{N} \text {(KE)}
6. \mathrm{B} \text {(US)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
1.
\mathrm{S}
[\mathrm{NR})
2. \mathrm{N} [\mathrm{RS})
3. \mathrm{B} [\mathrm{US})
2. \mathrm{N} [\mathrm{RS})
3. \mathrm{B} [\mathrm{US})
4.
\mathrm{K}
[\mathrm{EN})
5. \mathrm{R} [\mathrm{KU})
6. \mathrm{U} [\mathrm{BS})
5. \mathrm{R} [\mathrm{KU})
6. \mathrm{U} [\mathrm{BS})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
1.
\mathrm{U}
(\mathrm{BS})
2. \mathrm{R} (\mathrm{SN})
3. \mathrm{E} (\mathrm{KN})
2. \mathrm{R} (\mathrm{SN})
3. \mathrm{E} (\mathrm{KN})
4.
\mathrm{S}
(\mathrm{NR})
5. \mathrm{B} (\mathrm{BS})
6. \mathrm{K} (\mathrm{UN})
5. \mathrm{B} (\mathrm{BS})
6. \mathrm{K} (\mathrm{UN})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Générateur d'exercices
Générateur d'exercices
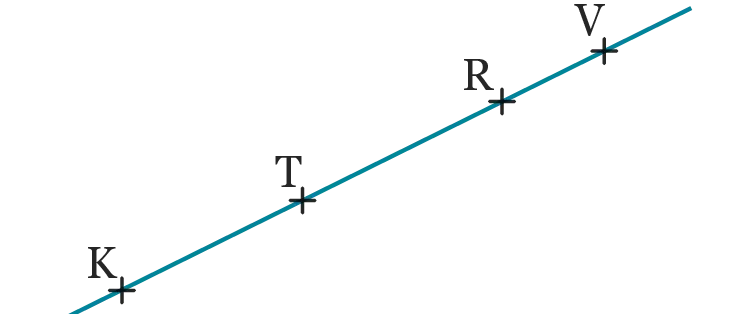
En utilisant la figure ci-dessous, compléter avec \mathrm{∈} ou \mathrm{∉}.



1.
\mathrm{T}
[\mathrm{RK})
2. \mathrm{K} (\mathrm{TR})
3. \mathrm{T} [\mathrm{KR})
4. \mathrm{R} [\mathrm{KR})
5. \mathrm{T} (\mathrm{RV})
2. \mathrm{K} (\mathrm{TR})
3. \mathrm{T} [\mathrm{KR})
4. \mathrm{R} [\mathrm{KR})
5. \mathrm{T} (\mathrm{RV})
6.
\mathrm{V}
[\mathrm{RT})
7. \mathrm{V} [\mathrm{RV})
8. \mathrm{V} (\mathrm{TK})
9. \mathrm{K} [\mathrm{TV})
7. \mathrm{V} [\mathrm{RV})
8. \mathrm{V} (\mathrm{TK})
9. \mathrm{K} [\mathrm{TV})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
On considère la figure ci-dessous.

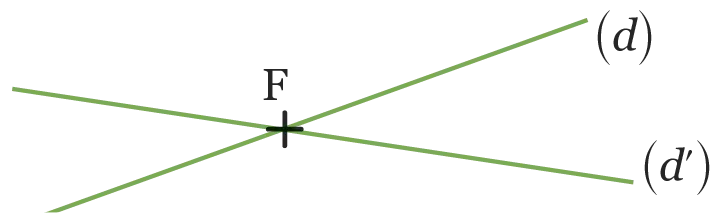
Compléter les phrases suivantes.
1. Les droites et sont sécantes en .
2. Le point \mathrm{F} est le des droites et .
3. \mathrm{F} (d) et \mathrm{F} \left(d^{\prime}\right).


Compléter les phrases suivantes.
1. Les droites
2. Le point \mathrm{F} est le
3. \mathrm{F}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
1. Placer trois points distincts non
alignés et les nommer \mathrm{K}, \mathrm{L} et \mathrm{M}.
2. Nommer et tracer toutes les droites
possibles avec ces trois points.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
On considère la figure ci-dessous.

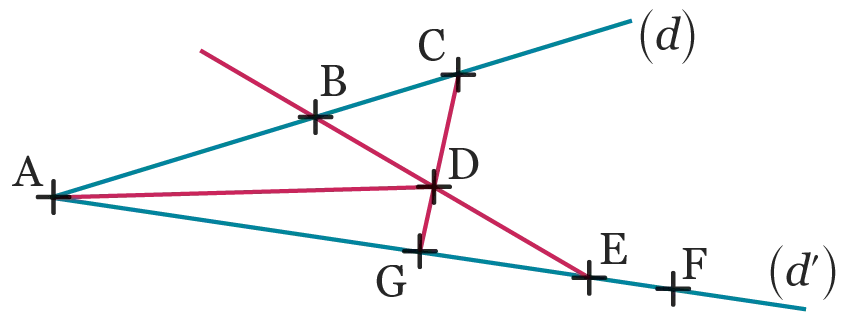
Écrire les noms de cinq droites différentes et de cinq demi-droites différentes.


Écrire les noms de cinq droites différentes et de cinq demi-droites différentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Exercice inversé
Exercice inversé
Proposer une figure telle que
les conditions suivantes soient
respectées.
\mathrm{C ∈ [BA)}, \mathrm{D ∈ (AB)}, \mathrm{E ∉ (AB)}, \mathrm{D ∉ [BA)} et \mathrm{C ∈ [AB)}.
\mathrm{C ∈ [BA)}, \mathrm{D ∈ (AB)}, \mathrm{E ∉ (AB)}, \mathrm{D ∉ [BA)} et \mathrm{C ∈ [AB)}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
1. On considère la figure suivante
2. D'après les informations suivantes,
retrouver le nom de chacun des points.
a. \mathrm{Z∈(IY)} mais \mathrm{Z} \notin[\mathrm{YI}).
b. \mathrm{G} \in[\mathrm{IY}) et \mathrm{G} \notin[\mathrm{YZ}).
c. \mathrm{Y∈(BE)} et \mathrm{E} \notin \mathrm{[YB)}.
a. \mathrm{Z∈(IY)} mais \mathrm{Z} \notin[\mathrm{YI}).
b. \mathrm{G} \in[\mathrm{IY}) et \mathrm{G} \notin[\mathrm{YZ}).
c. \mathrm{Y∈(BE)} et \mathrm{E} \notin \mathrm{[YB)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Segment et longueur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37À l'oral
À l'oral
On considère les points \mathrm{A}, \mathrm{T} et
\mathrm{R} tels que \mathrm{A∈ [TR]}, \mathrm{AR}=2,6 \mathrm{~cm} et \mathrm{AT}=3 \mathrm{~cm}. Calculer la longueur \mathrm{TR}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38À l'oral
À l'oral
\mathrm{G}, \mathrm{H} et \mathrm{I} sont trois points tels que
\mathrm{G ∉ [HI]}. Que peut-on dire de \mathrm{HG + GI}
par rapport à \mathrm{HI} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39À l'oral
À l'oral
Quelles informations nous donne
la phrase suivante ? « Le point \mathrm{K} est le
milieu du segment \mathrm{[UW]}. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40À l'oral
À l'oral
On considère le milieu \mathrm{I} du segment \mathrm{[TR]}. Dans chaque cas, justifier si l'égalité est vraie ou fausse.
1. \mathrm{IT = IR}
2. \mathrm{TI = TR}
3. \mathrm{TI}=\frac{1}{2} \mathrm{TR}
4. \mathrm{RT = RI}
5. 2 \times \mathrm{IR}=\mathrm{TR}
6. 2 \times \mathrm{IT}=\mathrm{RT}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Générateur d'exercices
Générateur d'exercices
\mathrm{A}, \mathrm{B} et \mathrm{C} sont trois points tels que \mathrm{AB}=7 \mathrm{~cm}, \mathrm{BC}=12 \mathrm{~cm} et \mathrm{AC}=19 \mathrm{~cm}.
Compléter avec ∈ ou ∉.
1. \mathrm{A} [\mathrm{BC}]
2. \mathrm{B} [\mathrm{AC}]
3. \mathrm{C} [\mathrm{AB}]
1. \mathrm{A} [\mathrm{BC}]
2. \mathrm{B} [\mathrm{AC}]
3. \mathrm{C} [\mathrm{AB}]
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
\mathrm{G}, \mathrm{R} et \mathrm{U} sont trois points tels que
\mathrm{GR}=4,5 \mathrm{~m}, \mathrm{GU}=10 \mathrm{~m} et \mathrm{RU}=5,5 \mathrm{~m}.
Compléter avec \mathrm{∈} ou ∉.
1. \mathrm{G} [\mathrm{RU})
2. \mathrm{U} (\mathrm{GR})
3. \mathrm{R} (\mathrm{GU})
1. \mathrm{G} [\mathrm{RU})
2. \mathrm{U} (\mathrm{GR})
3. \mathrm{R} (\mathrm{GU})
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
On considère les points \mathrm{N}, \mathrm{O} et \mathrm{T} tels
que \mathrm{N} \in[\mathrm{OT}],
\mathrm{OT}=7 \mathrm{~cm} et \mathrm{NT}=1 \mathrm{~cm}.
Calculer la longueur \mathrm{NO}.
Calculer la longueur \mathrm{NO}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Deux points \mathrm{H} et \mathrm{T} sont distants de
7 \mathrm{~cm}. \mathrm{J} est le milieu du segment \mathrm{[TH]}.
Calculer la longueur \mathrm{JT}.
Calculer la longueur \mathrm{JT}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
1. Sans utiliser d'instrument de
géométrie, comparer la longueur des
segments \mathrm{[AB]} et \mathrm{[BC]}.

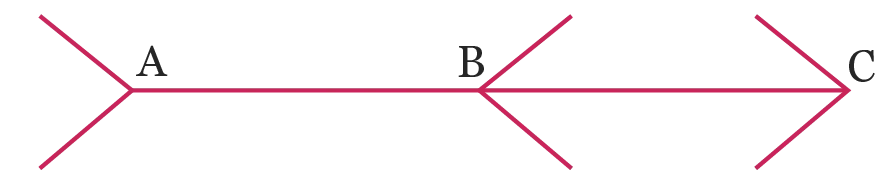
2. Vérifier la réponse donnée avec un
instrument de géométrie.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
1. On considère la figure suivante.
2. À l'aide du compas :
a. Justifier que \mathrm{CH}=3 \times \mathrm{AB}.
b. Exprimer \mathrm{HD} en fonction de \mathrm{AB}.
c. Placer le point \mathrm{V} sur \mathrm{[CD]} tel que
\mathrm{DV}=3 \times \mathrm{AB}.
d. Exprimer \mathrm{CV} en fonction de \mathrm{AB}.
Cliquez pour accéder à GeoGebra
a. Justifier que \mathrm{CH}=3 \times \mathrm{AB}.
d. Exprimer \mathrm{CV} en fonction de \mathrm{AB}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
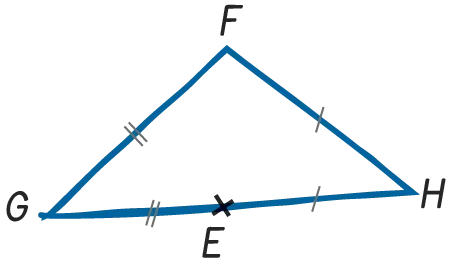
Kenzi a recopié rapidement la figure
tracée au tableau en fin d'heure.
Que peut-on en penser?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Tracer deux segments \mathrm{[KJ]} et \mathrm{[MN]}
ayant le même milieu \mathrm{R}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Tracer deux segments perpendiculaires
\mathrm{[SB]} et \mathrm{[IJ]} ayant le même milieu \mathrm{K}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
Réaliser la construction suivante.
1. Placer des points \mathrm{M}, \mathrm{I}, \mathrm{L} et \mathrm{O} distincts tels que jamais trois de ces points n'appartiennent à la même droite.
2. Tracer les segments \mathrm{[MI]}, \mathrm{[LO]} et \mathrm{[OI]}.
3. Placer les points \mathrm{J}, \mathrm{K}, et \mathrm{N}, milieux respectifs de \mathrm{[MI]}, \mathrm{[LO]} et \mathrm{[OI]}.
1. Placer des points \mathrm{M}, \mathrm{I}, \mathrm{L} et \mathrm{O} distincts tels que jamais trois de ces points n'appartiennent à la même droite.
2. Tracer les segments \mathrm{[MI]}, \mathrm{[LO]} et \mathrm{[OI]}.
3. Placer les points \mathrm{J}, \mathrm{K}, et \mathrm{N}, milieux respectifs de \mathrm{[MI]}, \mathrm{[LO]} et \mathrm{[OI]}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Mathéo a réalisé cette figure mais il a
oublié comment il l'a faite.

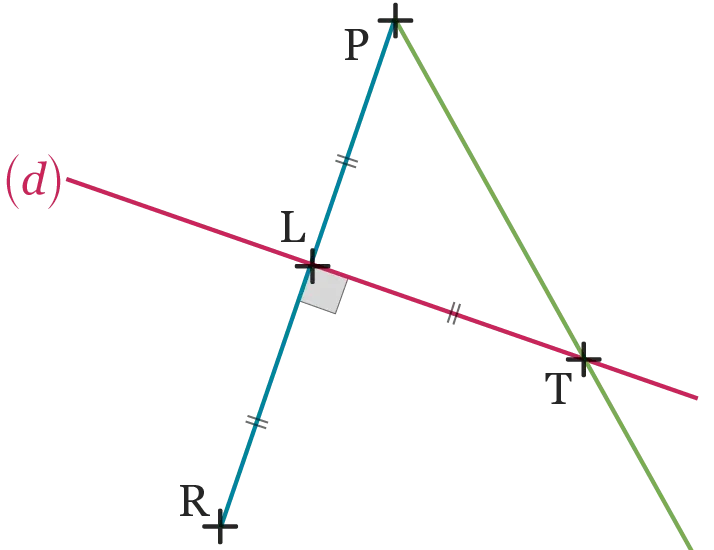
Aider Mathéo à réécrire un programme de construction.


Aider Mathéo à réécrire un programme de construction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
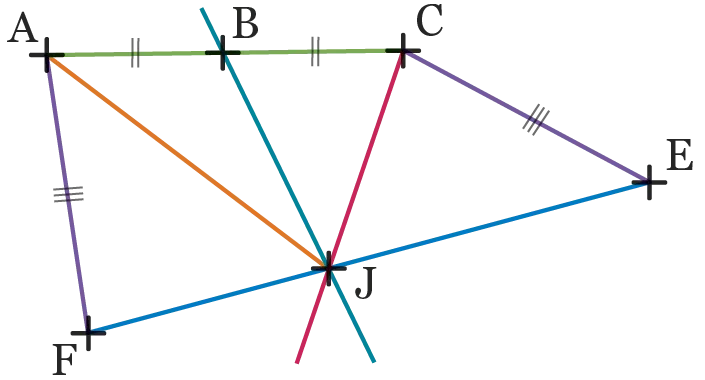
52
Proposer un programme de
construction permettant de construire la
figure suivante.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Copie d'élève
Copie d'élève
On souhaite réaliser la figure ci-dessous.

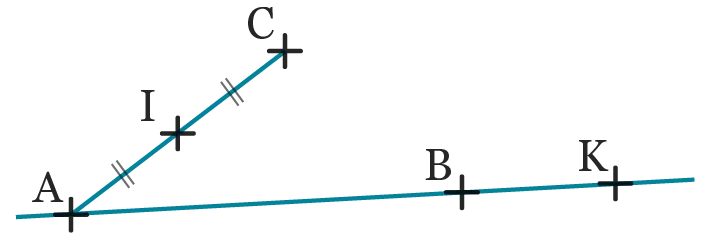
Voici ce que propose Léa.


Voici ce que propose Léa.
\mathrm{A}, \mathrm{B} et \mathrm{C} sont trois points tels que \mathrm{A∈ (BC)}.
\mathrm{I} est le milieu de \mathrm{(AC)}.
Placer le point \mathrm{K} de sorte que \mathrm{KB
Retrouver toutes les erreurs en les expliquant.\mathrm{I} est le milieu de \mathrm{(AC)}.
Placer le point \mathrm{K} de sorte que \mathrm{KB
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Comparer les périmètres des figures
bleue et rouge suivantes.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Calculer le périmètre des figures
suivantes.
1. Un losange de côté 3,6~\mathrm{cm}.
2. Un carré de côté 2,9~\mathrm{mm}.
3. Un pentagone régulier de côté 281~\mathrm{m}.
1. Un losange de côté 3,6~\mathrm{cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
Construire trois rectangles différents
dont le périmètre est 16~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
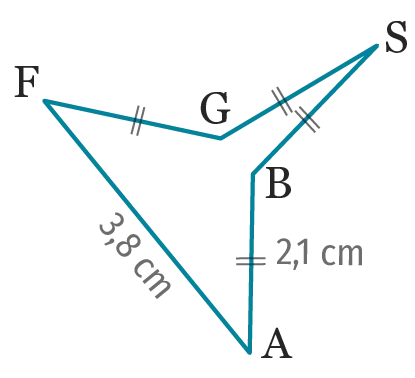
Quel est le périmètre de \mathrm{FGSBA} ?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
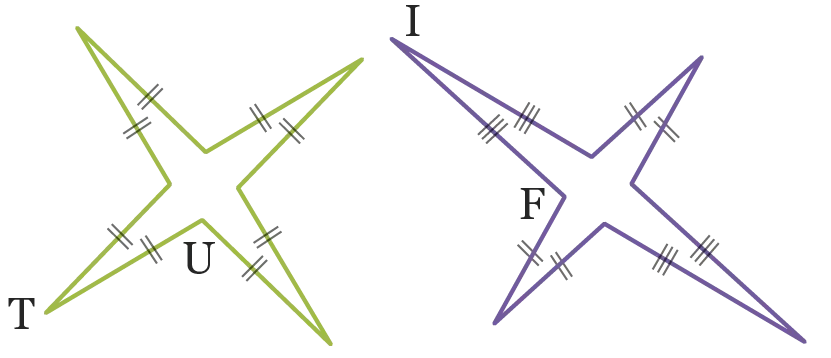
58
Calculer les périmètres des deux figures
suivantes sachant que \mathrm{TU}=3,6~\mathrm{cm} et
\mathrm{IF}=4,8~\mathrm{cm}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Un gourmand a mangé sa tablette de
chocolat de manière étrange.
1. Calculer le périmètre de la partie restante.

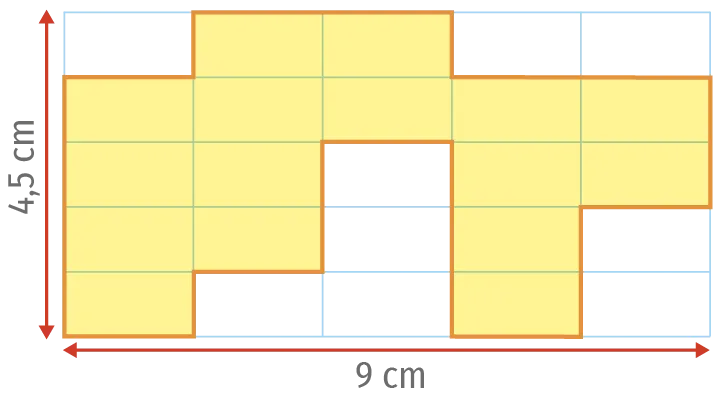 2. Comparer le résultat avec le périmètre de
la tablette entière.
2. Comparer le résultat avec le périmètre de
la tablette entière.
1. Calculer le périmètre de la partie restante.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
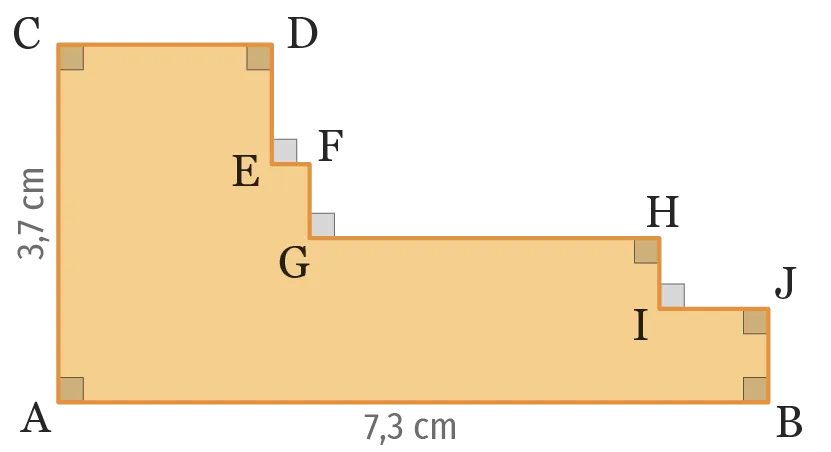
Calculer le périmètre de la figure
suivante.



Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

