Chapitre 14
Entraînement
Cercles et disques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cercles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
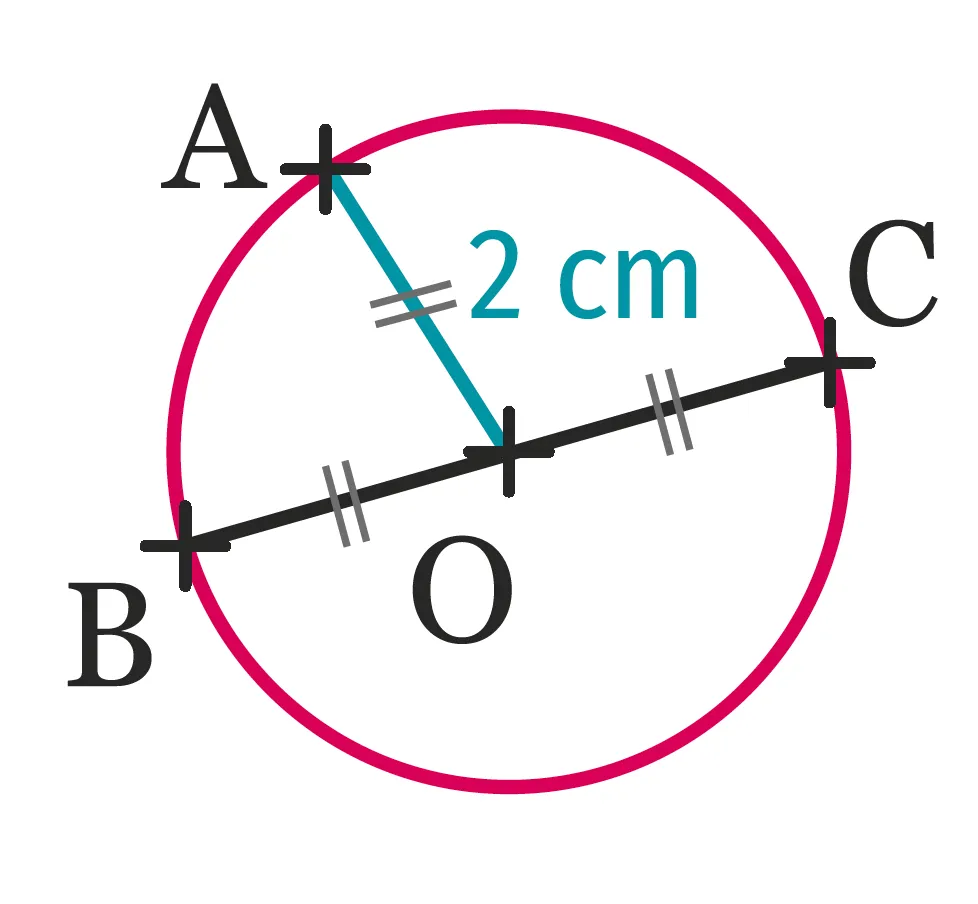
15À l'oral
À l'oral
Décrire la figure
suivante en utilisant
le vocabulaire adapté.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
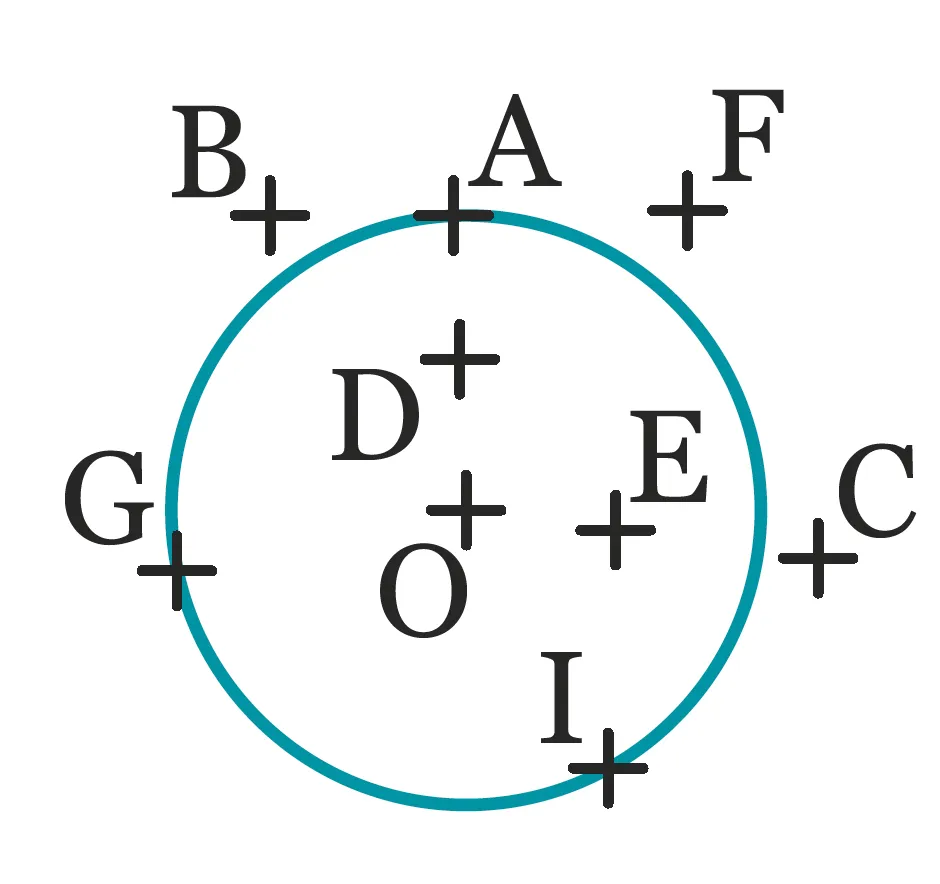
16À l'oral
À l'oral
Pour chaque point
de la figure, dire s'il
appartient au cercle de
centre \mathrm{O} et de rayon
\mathrm{OA}.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17À l'oral
À l'oral
Répondre par vrai ou faux. Justifier
et corriger les phrases fausses.
1. Si \mathrm{A} et \mathrm{B} sont deux points sur le cercle de centre \mathrm{O} et de rayon 5~\mathrm{cm} alors \mathrm{AB}=5 \mathrm{~cm}.
2. Le rayon est toujours le double du
diamètre.
3. Un diamètre est une corde.
1. Si \mathrm{A} et \mathrm{B} sont deux points sur le cercle de centre \mathrm{O} et de rayon 5~\mathrm{cm} alors \mathrm{AB}=5 \mathrm{~cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18À l'oral
À l'oral
Répondre par vrai ou faux. Justifier et corriger les phrases fausses.
1. La longueur d'un cercle correspond à son diamètre.
2. En connaissant la longueur d'une corde
quelconque, on peut calculer la longueur
du cercle.
3. Pour calculer la longueur d'un cercle
de diamètre \mathrm{D}, on utilise la formule
\mathrm{P}=\pi \times \mathrm{D} \times 2.
1. La longueur d'un cercle correspond à son diamètre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
1. Placer un point \mathrm{U} sur une feuille.
2. Placer tous les points qui sont à 4,5~ \mathrm{cm}du point \mathrm{U}.
3. Qu'a-t-on tracé ?
2. Placer tous les points qui sont à 4,5~ \mathrm{cm}du point \mathrm{U}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
1. Construire un cercle C de centre \mathrm{F} et de rayon 6~\mathrm{cm}.
2. Tracer en rouge un rayon de ce cercle.
3. Tracer en vert un diamètre de ce cercle.
4. Tracer en noir une corde de ce cercle.
2. Tracer en rouge un rayon de ce cercle.
3. Tracer en vert un diamètre de ce cercle.
4. Tracer en noir une corde de ce cercle.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Soit C_1 le cercle de centre \mathrm{L} et C_₂ le
cercle de centre \mathrm{A}. Compléter par \in ou \notin.

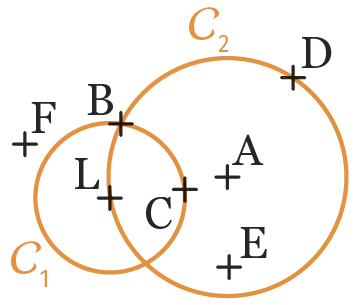

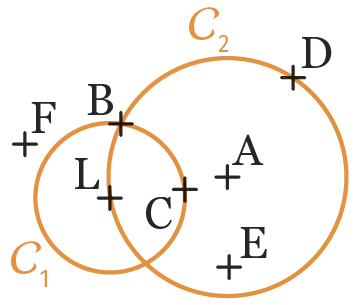
1. \mathrm{D} C₂
2. \mathrm{A} C₂
3. \mathrm{B} C₁
4. \mathrm{E} C₂
5. \mathrm{F} C₁
6. \mathrm{L} C₂
2. \mathrm{A}
3. \mathrm{B}
4. \mathrm{E}
5. \mathrm{F}
6. \mathrm{L}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
On souhaite
construire la figure
suivante avec
\mathrm{AR}=3,2 \mathrm{~cm}.

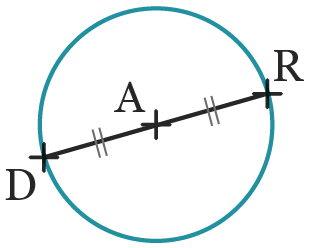
1. Compléter le programme de construction suivant.
a. Construire le segment de longueur \mathrm{cm}.
b. Construire, le milieu du segment .
c. À l'aide d'un, construire le cercle de \mathrm{A}
et de \mathrm{AR}.
2. Construire la figure en vraie grandeur.


1. Compléter le programme de construction suivant.
a. Construire le segment
b. Construire
c. À l'aide d'un
2. Construire la figure en vraie grandeur.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
1. Placer deux points distincts \mathrm{A} et \mathrm{B}
tels que \mathrm{AB}=7 \mathrm{~cm}.
2. Construire le cercle de centre \mathrm{A} et de rayon 3,6~\mathrm{cm}.
3. Construire le cercle de centre \mathrm{B} et de rayon 5~\mathrm{cm}.
4. Existe-t-il des points qui soient à la fois à
3,6~\mathrm{cm} de \mathrm{A} et à 5~\mathrm{cm} de \mathrm{B} ? Justifier.
5. Refaire toutes les questions précédentes
mais, cette fois, avec \mathrm{AB}=10 \mathrm{~cm} (les autres
longueurs de l'énoncé ne changent pas).
2. Construire le cercle de centre \mathrm{A} et de rayon 3,6~\mathrm{cm}.
3. Construire le cercle de centre \mathrm{B} et de rayon 5~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
1. Construire un segment [\mathrm{AB}] de
longueur 6~\mathrm{cm}.
2. a. Construire un cercle C_1 de centre \mathrm{A} ne passant pas par \mathrm{B}.
b. Construire le cercle C_2 de centre \mathrm{B} et de rayon 4~\mathrm{cm}.
c. Construire un cercle C_3 de rayon \mathrm{AB}.
d. Construire le cercle C_4 de diamètre \mathrm{[AB]}
2. a. Construire un cercle C_1 de centre \mathrm{A} ne passant pas par \mathrm{B}.
b. Construire le cercle C_2 de centre \mathrm{B} et de rayon 4~\mathrm{cm}.
c. Construire un cercle C_3 de rayon \mathrm{AB}.
d. Construire le cercle C_4 de diamètre \mathrm{[AB]}
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Copie d'élève
Copie d'élève
Le professeur a demandé de
construire un cercle \mathrm{C} de centre \mathrm{K} et de
diamètre 5~\mathrm{cm}.
Voici la copie de Xavier.

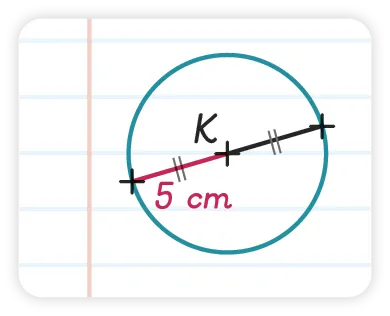 Reproduire la figure
en corrigeant son
erreur.
Reproduire la figure
en corrigeant son
erreur.
Voici la copie de Xavier.


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Chloé et Axelle jouent à un jeu où un
totem doit être équidistant des joueurs.


1.
a. Placer deux points \mathrm{A} et \mathrm{C} correspondant
aux positions d'Axelle et de Chloé.
b. Placer un point \mathrm{T} représentant une position possible du totem.
2. a. Giulia souhaite rejoindre la partie. Représenter tous les endroits possibles oû Giulia peut s'installer en respectant la règle de placement.
b. Décrire la figure obtenue.
b. Placer un point \mathrm{T} représentant une position possible du totem.
2. a. Giulia souhaite rejoindre la partie. Représenter tous les endroits possibles oû Giulia peut s'installer en respectant la règle de placement.
Cliquez pour accéder à GeoGebra


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
1. Construire un cercle passant par deux
points distincts.
2. Existe-t-il d'autres cercles passant par ces deux mêmes points ?
Cliquez pour accéder à GeoGebra
2. Existe-t-il d'autres cercles passant par ces deux mêmes points ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Donner, en cm, la valeur exacte puis un
arrondi au dixième près de la longueur du
cercle de :
1. 4,5\mathrm{~cm} de rayon ;
2. 7,5\mathrm{~cm} de diamètre ;
3. 6\mathrm{~m} de diamètre.
1. 4,5\mathrm{~cm} de rayon ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Donner, en cm, la valeur exacte puis un
arrondi au dixième près de la longueur du
demi-cercle de :
1. 3,7~\mathrm{cm} de diamètre ;
2. 8,2~\mathrm{cm} de rayon.
1. 3,7~\mathrm{cm} de diamètre ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
L'équateur est une ligne imaginaire
faisant le tour de la Terre. On le modélise
par un cercle.
Sachant que le rayon de la Terre est de 6~378~\mathrm{km}, calculer la longueur de l'équateur arrondi au dixième de kilomètre.

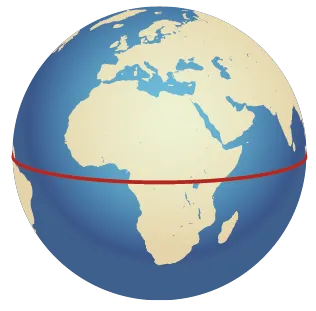
Sachant que le rayon de la Terre est de 6~378~\mathrm{km}, calculer la longueur de l'équateur arrondi au dixième de kilomètre.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Exercice inversé
Exercice inversé
À partir de la figure ci-dessous,
un élève a donné la réponse
suivante : \mathrm{L} \approx 31,4 \mathrm{~cm}.
Retrouver quelle aurait pu
être la consigne.

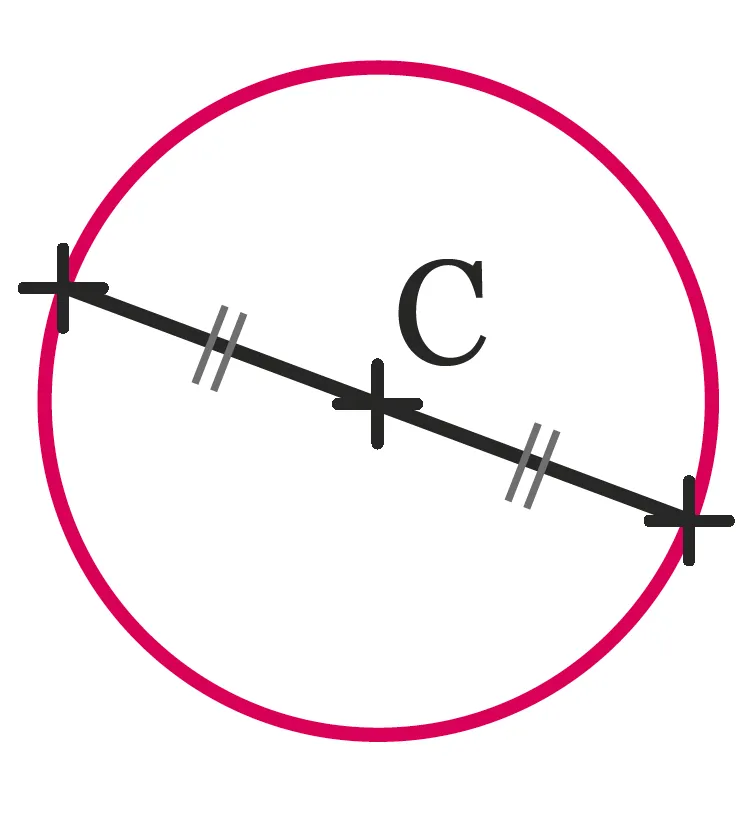


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Une grande roue a un rayon de 20~\mathrm{m}.
Quand une nacelle fait trois tours complets, quelle distance a-t-elle parcourue ?
Arrondir au mètre près.
Quand une nacelle fait trois tours complets, quelle distance a-t-elle parcourue ?
Arrondir au mètre près.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Mariam veut acheter une bague de 2~\mathrm{cm}
de diamètre. Elle souhaite la mettre à son
annulaire qui a un tour de 6~\mathrm{cm}. Pourra-t-elle
mettre la bague ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Disques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
À l'oral
Parmi les objets suivants, lesquels
peuvent être modélisés par un disque ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35À l'oral
À l'oral
La photo suivante représente un disque compact. Porte-t-il bien son nom ? Justifier.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36À l'oral
À l'oral
Parmi les figures ci-dessous, quelles
sont celles pour lesquelles on a colorié
un disque de centre \mathrm{A} ?

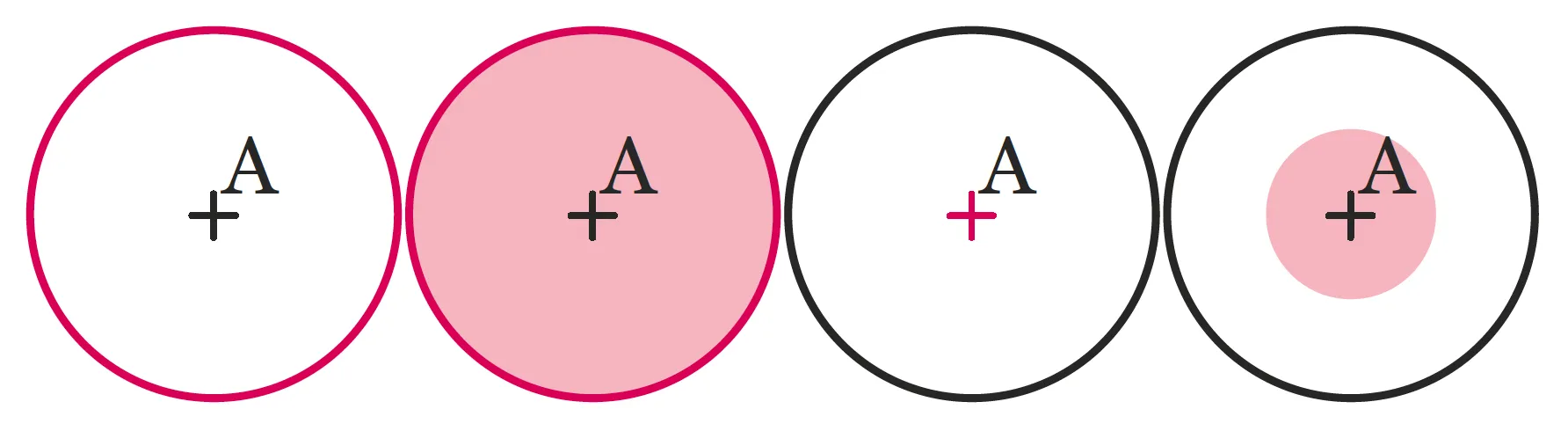

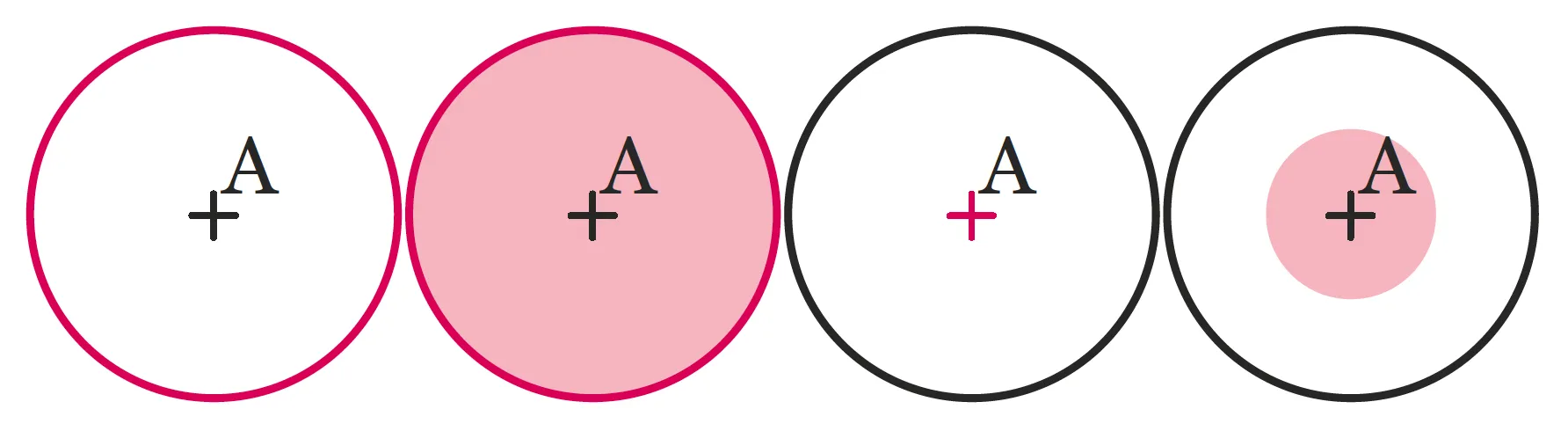
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37Générateur d'exercices
Générateur d'exercices
On a représenté le cercle de
centre \mathrm{K} et de rayon
3,6~\mathrm{cm}.
Compléter avec les
symboles <, = ou >.

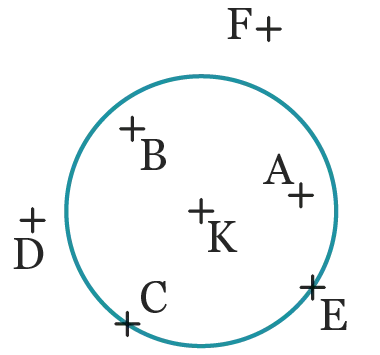
1. \mathrm{KA}
2. \mathrm{KB}
3. \mathrm{KC}
4. \mathrm{KD}
5. \mathrm{KE}
6. \mathrm{KF}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
En physique, le cercle chromatique est la
représentation graphique de la décompositior
des teintes du spectre lumineux.
La synthèse
additive des
lumières est
donnée par la figure suivante.

1. Décrire la figure en utilisant les mots cercle, disque et centre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
1. a. Construire un segment \mathrm{[AB]} de
longueur 5~\mathrm{cm}.
b. Construire un cercle C_1 de centre \mathrm{A} tel que \mathrm{B} n'appartienne pas au disque délimité par C_1.
c. Construire un cercle C_2 de centre \mathrm{B} tel que \mathrm{A} appartienne au disque délimité par C_2.
2 Colorier l'ensemble des points appartenant aux deux disques délimités par C_1 et C_2.
b. Construire un cercle C_1 de centre \mathrm{A} tel que \mathrm{B} n'appartienne pas au disque délimité par C_1.
c. Construire un cercle C_2 de centre \mathrm{B} tel que \mathrm{A} appartienne au disque délimité par C_2.
2 Colorier l'ensemble des points appartenant aux deux disques délimités par C_1 et C_2.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
1. Construire un segment \mathrm{[PA]} de
longueur 10~\mathrm{cm}.
2. Construire le cercle C_1 de diamètre \mathrm{[PA]}. On appellera \mathrm{K} le centre de ce cercle.
3. Construire le cercle C_2 de centre \mathrm{K} et de rayon 1,3~\text{cm}.
4 Colorier en rouge les points appartenant au disque C_1, mais n'appartenant pas au disque C_2.
2. Construire le cercle C_1 de diamètre \mathrm{[PA]}. On appellera \mathrm{K} le centre de ce cercle.
3. Construire le cercle C_2 de centre \mathrm{K} et de rayon 1,3~\text{cm}.
4 Colorier en rouge les points appartenant au disque C_1, mais n'appartenant pas au disque C_2.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
On modélise un pare-brise arrière d'une
voiture par un rectangle de longueur 80~\mathrm{cm}
et de largeur 30~\mathrm{cm}. On fixe un essuie-glace
au milieu de la longueur.
1. Quelle est la longueur maximale que peut faire l'essuie-glace ?
2. On choisit un essuie-glace de 25~\mathrm{cm}
de long. En prenant 1 carreau pour 5~\mathrm{cm},
représenter la zone balayée par l'essuie-glace.
1. Quelle est la longueur maximale que peut faire l'essuie-glace ?
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42Exercice inversé
Exercice inversé
On donne \mathrm{AB}=3 \mathrm{~cm}.
Écrire la consigne d'un exercice qui a permis d'obtenir la figure suivante.

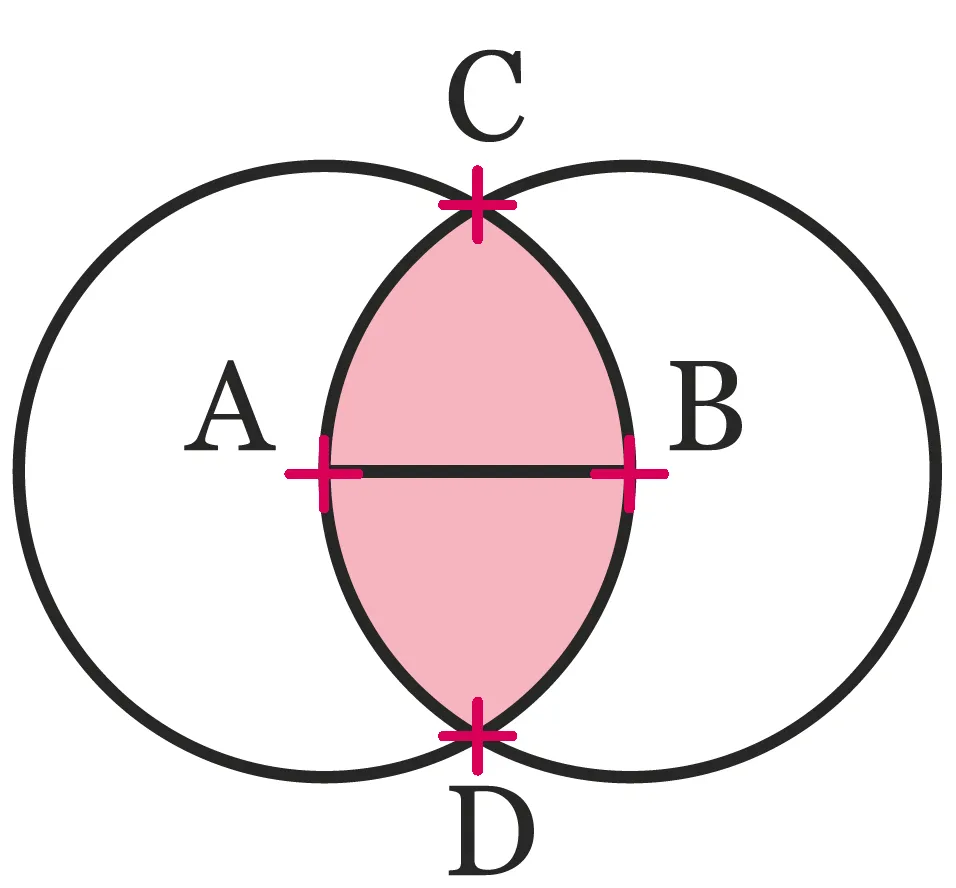
Écrire la consigne d'un exercice qui a permis d'obtenir la figure suivante.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43Environnement
Environnement
Les cernes de croissance
d'un arbre peuvent être assimilés
à des anneaux qui apparaissent
lors des saisons de croissance :
printemps et été (anneaux blanchâtres)
et automne et hiver (anneaux foncés).




1. Tracer un cercle de centre \mathrm{A} et de
rayon 2~\mathrm{cm} puis un cercle de centre \mathrm{A} et de rayon 2,5~\mathrm{cm}. L'espace entre les deux
représente un anneau.
2. Continuer de tracer des cercles de centre \mathrm{A} en augmentant le rayon de 0,5~\mathrm{cm} à chaque fois, jusqu'à atteindre 6~\mathrm{cm} de rayon.
3. Colorier un anneau sur deux.
4. Combien de saisons de croissance
a connu l'arbre modélisé par la figure
obtenue ?
2. Continuer de tracer des cercles de centre \mathrm{A} en augmentant le rayon de 0,5~\mathrm{cm} à chaque fois, jusqu'à atteindre 6~\mathrm{cm} de rayon.
3. Colorier un anneau sur deux.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
On souhaite réaliser un chapeau
d'anniversaire en forme de cône pour une
personne dont le tour de tête est de 55~\mathrm{cm}.
On utilise le patron suivant. Le chapeau sera-t-il suffisamment grand ?

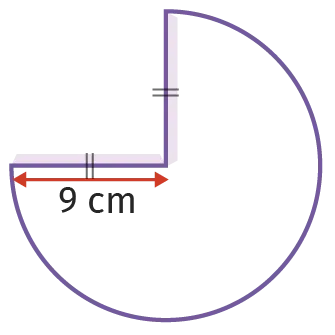
On utilise le patron suivant. Le chapeau sera-t-il suffisamment grand ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
Calculer, en cm, le périmètre de la figure
suivante.
Donner la valeur exacte puis la valeur arrondie au dixième.

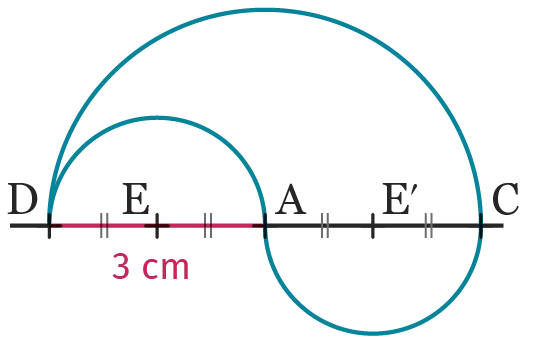
Donner la valeur exacte puis la valeur arrondie au dixième.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Calculer, en cm, le périmètre de la figure
suivante. Donner la valeur exacte puis la
valeur arrondie au dixième.

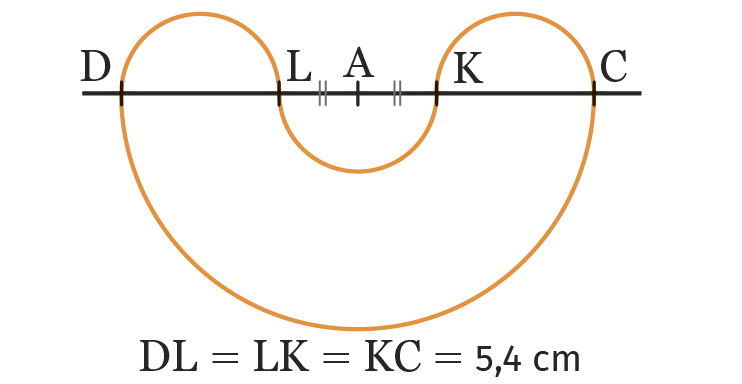


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
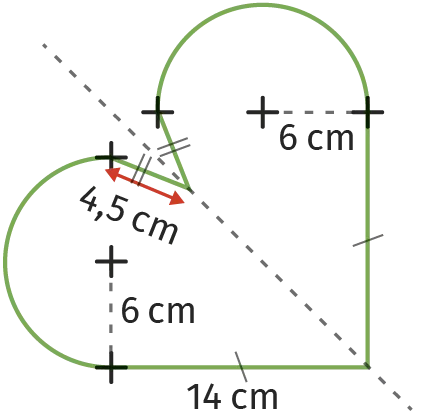
47
Calculer, en cm, le périmètre de la figure
suivante. Donner la valeur exacte puis la
valeur arrondie au dixième.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
À l'intérieur du disque \mathrm{D} de centre \mathrm{O}
et de diamètre \mathrm{MN}=20 \mathrm{~cm}, on a construit
quatre disques de diamètre 10 \mathrm{~cm} comme le
montre la figure ci-dessous.

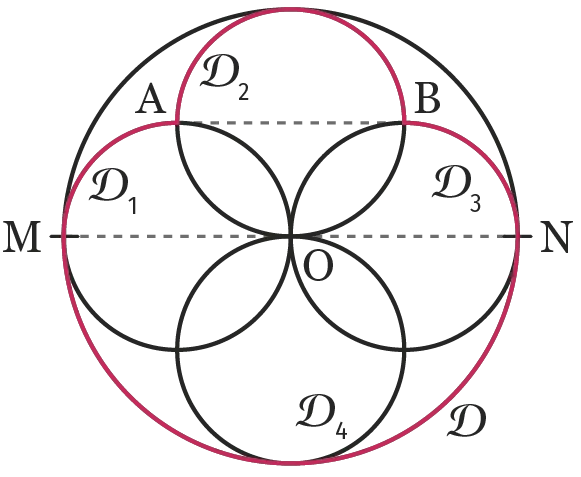
Calculer le périmètre de la figure délimitée par la ligne rouge.


Calculer le périmètre de la figure délimitée par la ligne rouge.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


