Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Synthèse
Aires et volumes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
Les pièces suivantes sont constituées de
carrés identiques de 3~\mathrm{mm} de côté.
1. Calculer l'aire de chacune de ces pièces.
2. Quelles pièces ont la plus grande aire ?
1. Calculer l'aire de chacune de ces pièces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
1. Calculer la longueur exacte d'un rectangle
de largeur 17~\mathrm{mm} et d'aire 25~\mathrm{cm}^2.
2. Encadrer la mesure trouvée en millimètre
par deux nombres entiers consécutifs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
1. Quelle est l'aire en \mathrm{mm^2} d'un carré de périmètre 14,44~\mathrm{cm} ?
2. Quelle est l'aire en \mathrm{cm^2} d'un rectangle de longueur 6,3~ \mathrm{dm} dont le périmètre mesure 20~\mathrm{dm} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
L'aire d'un rectangle est de 60 unités d'aire.
Sachant que les longueurs de ses côtés sont
entières, quelles sont toutes les mesures de
périmètres possibles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Le maire d'une petite ville souhaite paver
la place de la mairie qui a une fontaine
carrée au centre. La place est rectangulaire
et ses dimensions sont 26,5~\mathrm{m} et 17,4~\mathrm{m}. Le
périmètre de la fontaine est égal à 1~644~\mathrm{cm}.
1. Faire un schéma de la situation.
2. Quelle surface doit être pavée ?
3. On choisit des pavés droits qui mesurent
20~\mathrm{cm} de longueur et 14~\mathrm{cm} de largeur. Donner un ordre de grandeur du nombre de
pavés nécessaires.
1. Faire un schéma de la situation.
Cliquez ici pour avoir accès à un espace de dessin
2. Quelle surface doit être pavée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Pour l'anniversaire
de sa sœur, Kylian
veut lui offrir
une reproduction
miniature d'un Kroa
de Vasarely dont voici
une photo.
La reproduction tient dans un cube de 15~\mathrm{cm} de côté.
Kylian possède trois boîtes cubiques pour l'emballer. La première a un volume de 45~\mathrm{cm}^3, la seconde de 150~\mathrm{cm}^3 et la dernière de 3~375~\mathrm{cm}^3. Laquelle doit-il utiliser ?
La reproduction tient dans un cube de 15~\mathrm{cm} de côté.
Kylian possède trois boîtes cubiques pour l'emballer. La première a un volume de 45~\mathrm{cm}^3, la seconde de 150~\mathrm{cm}^3 et la dernière de 3~375~\mathrm{cm}^3. Laquelle doit-il utiliser ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
On augmente la longueur de chaque côté
d'un carré de 3~\mathrm{m}. L'aire obtenue est égale
à 100~\mathrm{m}^2. Quelle était l'aire du carré avant
l'augmentation de ses côtés ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Environnement
Environnement
Julia souhaite installer des
panneaux solaires sur le toit de sa
maison. Elle va installer des panneaux
rectangulaires de dimensions suivantes :
\ell~=~987,5~\mathrm{mm} et \mathrm{L}~=~1645,7~\mathrm{mm}.
1. Quelle est la superficie d'un panneau ?
2. Une surface de 1~\mathrm{m^2} de panneau
peut produire environ 250~\mathrm{kWh} par an.
Combien de panneaux solaires faut-il
installer au minimum pour compenser une
consommation annuelle de 3~500~\mathrm{kWh} ?
1. Quelle est la superficie d'un panneau ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Calculer l'aire du trapèze \mathrm{ABCD} suivant.
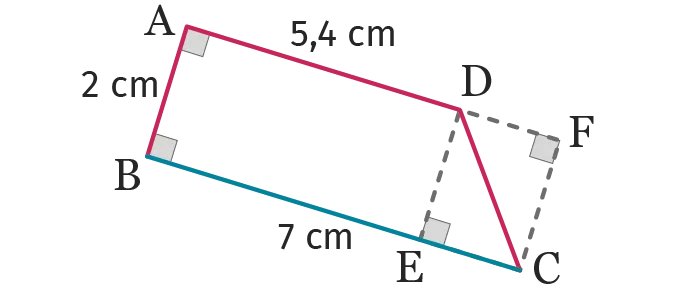
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
Joyce et Linda veulent refaire le sol de leur
salon. Celui-ci est rectangulaire, de largeur
5~\mathrm{m} et de longueur 8~\mathrm{m}.
Joyce veut mettre du parquet avec des lattes rectangulaires de dimensions 35~\mathrm{cm} de largeur et 120~\mathrm{cm} de longueur.
Linda préfère du carrelage avec des carreaux carrés de 1~600~\mathrm{cm^2}.
Dans chaque cas, calculer combien de lattes ou de carreaux vont être nécessaires au minimum sachant qu'il est possible de découper des carreaux et des lattes.
Joyce veut mettre du parquet avec des lattes rectangulaires de dimensions 35~\mathrm{cm} de largeur et 120~\mathrm{cm} de longueur.
Linda préfère du carrelage avec des carreaux carrés de 1~600~\mathrm{cm^2}.
Dans chaque cas, calculer combien de lattes ou de carreaux vont être nécessaires au minimum sachant qu'il est possible de découper des carreaux et des lattes.
Bonus
Une latte de plancher coûte 10,50~€
et un carreau de carrelage coûte 3,75~€. Quel
serait le coût de chacun des projets ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
On considère que
l'assemblage suivant n'est
pas creux. Chaque petit cube
a un volume de 1~\mathrm{cm^3}.
1. Quel est le volume de cet assemblage
en \mathrm{cm^3} ?
2. Calculer l'aire de la surface extérieure de
cet assemblage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
Melvin utilise des petits cubes empilables
pour construire un grand cube.
1. Chaque face du grand cube est constituée de seize petits cubes. Combien de petits cubes ont été utilisés au total pour faire le grand ?
2. Zara enlève un petit cube à chaque
sommet de l'assemblage. Combien de petits
cubes enlève-t-elle ?
3. Le volume d'un petit cube est de 1~\mathrm{cm}³.
Quel est le volume de l'assemblage final
en \mathrm{cm}³ ?
1. Chaque face du grand cube est constituée de seize petits cubes. Combien de petits cubes ont été utilisés au total pour faire le grand ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Le cube suivant est percé de part en part
(représenté en jaune sur le dessin).
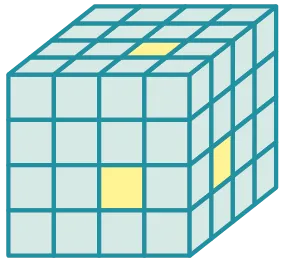Chaque petit cube a un volume de 1~\mathrm{cm}^3.
Calculer le volume du cube percé en \mathrm{cm}^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Un grand cube, constitué de
100 petits cubes sur chaque face,
est plongé dans de la peinture.
Combien de petits cubes seront
recouverts de peinture sur une
face ? Deux faces ? Trois faces ?
Quatre faces ? Cinq faces ? Six
faces ? Aucune face ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
On considère
l'assemblage suivant.
Tous les cubes qui
le composent sont
visibles. Chaque cube
a un volume de 1~\mathrm{cm}^3.
1. Quel est le volume
de cet assemblage ?
2. Quelle est l'aire de la surface de cet
assemblage ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
