Chapitre 10
Approfondissement
Théorème de Thalès et triangles semblables
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 19[Cal.4]
Sur la figure ci‑dessous, qui n'est pas à l'échelle, les droites (\mathrm{AB}) et (\mathrm{CD}) sont perpendiculaires en \text{O,} les droites (\mathrm{AC}) et (\mathrm{BD}) sont parallèles et, de plus, \mathrm{AO}=6 \mathrm{~cm}, \mathrm{OD}=4 \mathrm{~cm} et \mathrm{AC}=10 \mathrm{~cm}.

1. Calculer la longueur \text{OC.}
2. Soit \text{M} le milieu de [\mathrm{AC}]. Calculer \text{AM.}
3. Calculer la longueur \text{CD.}
4. Calculer la longueur \text{AB.}
5. Donner la longueur \text{OB.}
6. Calculer la longueur \text{BD.}
7. Remplacer les six nombres entiers trouvés par la lettre correspondant à son rang dans l'alphabet (\text{A} correspond au 1, \text{B} correspond au 2, etc.).
Le mot est :.

1. Calculer la longueur \text{OC.}
2. Soit \text{M} le milieu de [\mathrm{AC}]. Calculer \text{AM.}
3. Calculer la longueur \text{CD.}
4. Calculer la longueur \text{AB.}
5. Donner la longueur \text{OB.}
6. Calculer la longueur \text{BD.}
7. Remplacer les six nombres entiers trouvés par la lettre correspondant à son rang dans l'alphabet (\text{A} correspond au 1, \text{B} correspond au 2, etc.).
Le mot est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 20[Mod.5]
Le script Scratch ci‑dessous permet de dessiner la pale d'éolienne présente ci‑après où les longueurs sont en mètre.

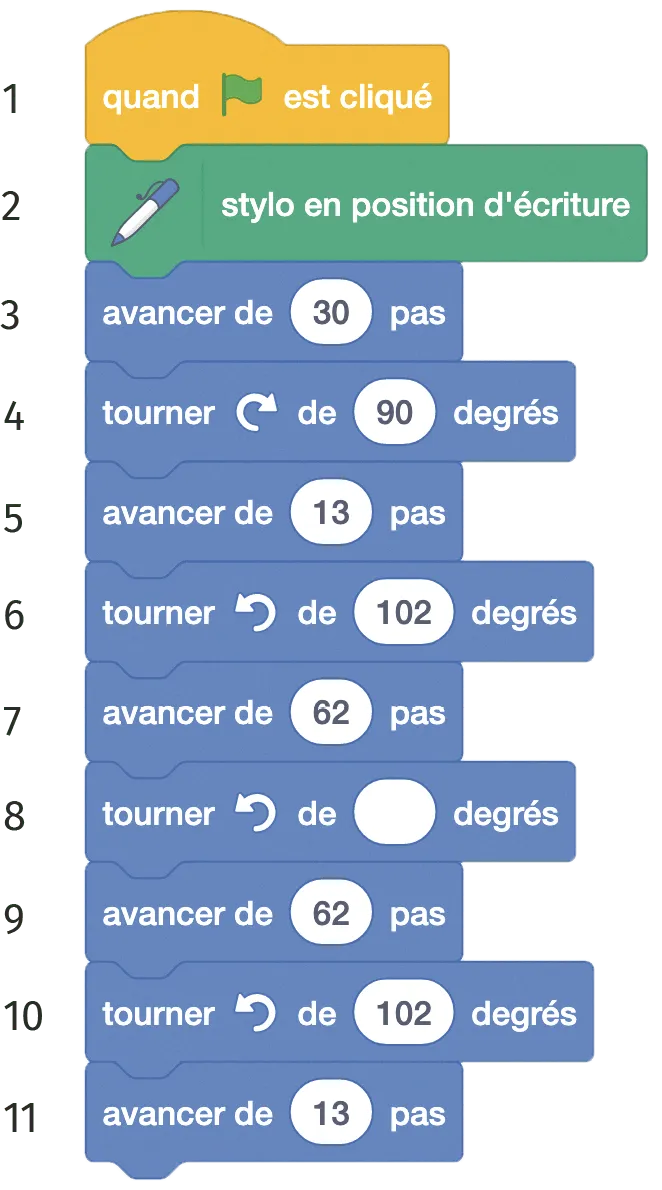

1. À l'aide du codage de la figure, que peut‑on dire du triangle \text{DEC} ?
2. Calculer la mesure de l'angle \widehat{\mathrm{CDE}}.
3. Pourquoi, à la ligne 6 du script, la mesure de l'angle est‑elle égale à 102° ?
4. Quelle valeur doit compléter la ligne 8 ?
5. Samantha souhaite construire une maquette de cette pale pour illustrer son exposé. La longueur \text{AB} doit mesurer 2,5 cm sur la maquette.
a. Déterminer la valeur du coefficient de réduction qu'elle doit appliquer aux longueurs réelles.
b.



1. À l'aide du codage de la figure, que peut‑on dire du triangle \text{DEC} ?
2. Calculer la mesure de l'angle \widehat{\mathrm{CDE}}.
3. Pourquoi, à la ligne 6 du script, la mesure de l'angle est‑elle égale à 102° ?
4. Quelle valeur doit compléter la ligne 8 ?
5. Samantha souhaite construire une maquette de cette pale pour illustrer son exposé. La longueur \text{AB} doit mesurer 2,5 cm sur la maquette.
a. Déterminer la valeur du coefficient de réduction qu'elle doit appliquer aux longueurs réelles.
b.
| Réalité | Maquette | |
|---|---|---|
| \mathbf{AB} | 30 m | 2,5 cm |
| \mathbf{CD} | ||
| \widehat{\mathbf{BCD}} | 78° | |
| \mathbf{CD} | ||
| Total |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 21
Inversé
[Rais.4 - Rais.5]
On donne la figure ci‑dessous, qui n'est pas à l'échelle.

Les mesures suivantes sont données en centimètre : \mathrm{AB}=2{,}4 ~; \mathrm{OB}=2~; \mathrm{OA}=1~; \mathrm{OC}=5~; \mathrm{OD}=2{,}5~; \mathrm{OM}=1{,}5~; \mathrm{ON}=0{,}9.
À l'aide du brouillon incomplet de Manon, retrouver les questions posées.
1. ?
Les points \text{B, O, C} d'une part et les points \text{A, O, D} d'autre part sont alignés dans le même ordre. On calcule les quotients \frac{\text{OB}}{\text{OC}}=\frac{2}{5} et \frac{\mathrm{OA}}{\mathrm{OD}}=\frac{1}{2{,}5}=\frac{2}{5}.
2. ?
Les droites \text{(BC)} et \text{(AD)} sont sécantes en \text{O} et les droites \text{(AB)} et \text{(CD)} sont parallèles.
D'après le théorème de Thalès, on peut écrire les égalités suivantes : \frac{\mathrm{OB}}{\mathrm{OC}}=\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{\mathrm{AB}}{\mathrm{CD}}.
On remplace par les valeurs numériques : \frac{2}{5}=\frac{2{,}4}{\mathrm{CD}}.
3. ?
Les points \text{O, N, D} d'une part et les points \text{O, M, C} d'autre part sont alignés.
On calcule les quotients \frac{\mathrm{OM}}{\mathrm{OC}}=\frac{1{,}5}{5}=0{,}3 et \frac{\mathrm{ON}}{\mathrm{OD}}=\frac{0{,}9}{2{,}5}=0{,}36.

Les mesures suivantes sont données en centimètre : \mathrm{AB}=2{,}4 ~; \mathrm{OB}=2~; \mathrm{OA}=1~; \mathrm{OC}=5~; \mathrm{OD}=2{,}5~; \mathrm{OM}=1{,}5~; \mathrm{ON}=0{,}9.
À l'aide du brouillon incomplet de Manon, retrouver les questions posées.
1.
Les points \text{B, O, C} d'une part et les points \text{A, O, D} d'autre part sont alignés dans le même ordre. On calcule les quotients \frac{\text{OB}}{\text{OC}}=\frac{2}{5} et \frac{\mathrm{OA}}{\mathrm{OD}}=\frac{1}{2{,}5}=\frac{2}{5}.
2.
Les droites \text{(BC)} et \text{(AD)} sont sécantes en \text{O} et les droites \text{(AB)} et \text{(CD)} sont parallèles.
D'après le théorème de Thalès, on peut écrire les égalités suivantes : \frac{\mathrm{OB}}{\mathrm{OC}}=\frac{\mathrm{OA}}{\mathrm{OD}}=\frac{\mathrm{AB}}{\mathrm{CD}}.
On remplace par les valeurs numériques : \frac{2}{5}=\frac{2{,}4}{\mathrm{CD}}.
3.
Les points \text{O, N, D} d'une part et les points \text{O, M, C} d'autre part sont alignés.
On calcule les quotients \frac{\mathrm{OM}}{\mathrm{OC}}=\frac{1{,}5}{5}=0{,}3 et \frac{\mathrm{ON}}{\mathrm{OD}}=\frac{0{,}9}{2{,}5}=0{,}36.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

