Rappels de seconde
Fonctions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions : généralités et variations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Une fonction f définie sur \mathcal{D} associe, à chaque réel x \in \mathcal{D}, un unique réel y , noté f(x).Il y a trois principaux modes de définition d'une fonction f :
- son expression f(x) en fonction de x\: ;
- un tableau de valeurs ;
- sa courbe représentative \mathcal{C}_f : ensemble des points \text{M}(x \:; f(x)).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
g(-1) = 02 admet pour antécédents 0 et 10 par g .


\text{A}(5\: ; 3) est un point de la courbe \mathcal{C}_g .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
f est dite croissante (resp. décroissante) sur \mathcal{D} lorsque, pour tous réels
a et b de \mathcal{D} tels que a \leqslant b , on a : f(a) \leqslant f(b) (resp. f(a) \geqslant f(b) ).f est dite monotone sur \mathcal{D} lorsqu'elle est soit croissante, soit décroissante sur \mathcal{D}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fonction carré est décroissante sur ]-\infty\: ; 0] et croissante sur [0 \:;+\infty[.On a : -3 \leqslant -1 donc f(-3) \geqslant f(-1).
La fonction racine carrée est monotone sur [0 \:;+\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
On dit que f admet un minimum (resp. un maximum) m (resp. \text{M}) sur \mathcal{D} en x = \alpha lorsque, pour tout x \in \mathcal{D}, f(x) \geqslant m (resp. f(x) \leqslant \text{M}) et f(\alpha) = m (resp. f(\alpha) = \text{M}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fonction carré admet 0 pour minimum sur \R , atteint pour x = 0 .Pour tout réel x , x^{2} \geqslant 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Soient f et g deux fonctions définies sur un ensemble \mathcal{D}. k est un réel. Graphiquement, les solutions de :
- f(x) \geqslant k sont les abscisses des points de \mathcal{C}_f dont l'ordonnée est supérieure ou égale à k \:;
- f(x) = g(x) sont les abscisses des points d'intersection de \mathcal{C}_f et \mathcal{C}_g \:;
- f(x) \geqslant g(x) sont les abscisses des points de \mathcal{C}_f situés au-dessus ou sur \mathcal{C}_g.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
f(x)\lt2 \Leftrightarrow x \in]-2\: ; 2[f(x) \geqslant g(x) \Leftrightarrow x \in]-\infty \:;-1,5] \cup[0\: ; 2]

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
On considère le tableau de variations d'une fonction f .

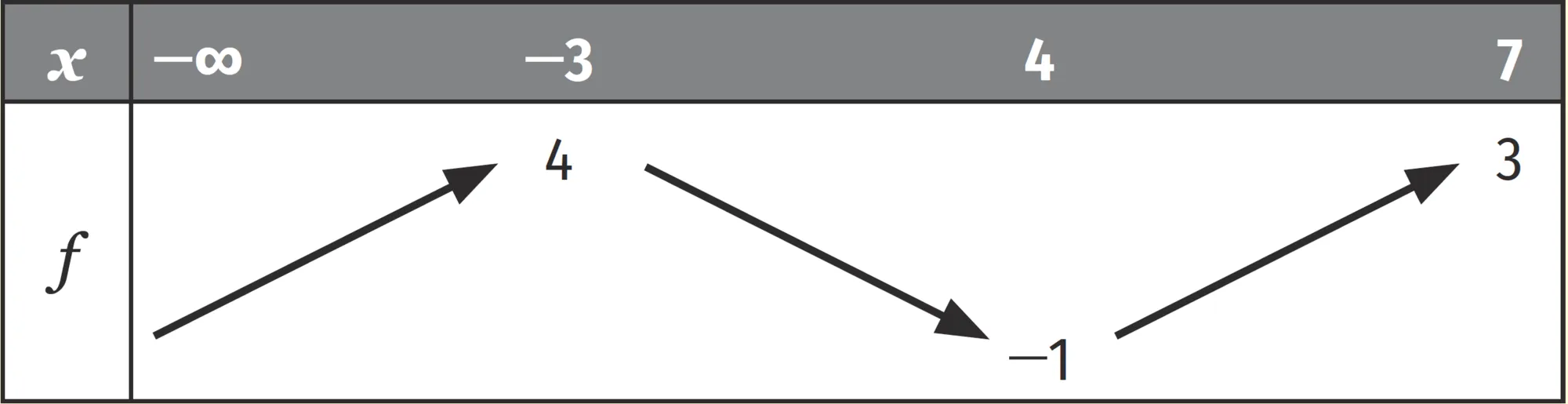
1. Déterminer l'ensemble de définition \mathcal{D} de f .
2. Décrire les variations de cette fonction sur \mathcal{D}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Soient f et g deux fonctions définies sur \R par leur
expression f(x) = x^2 et g(x) = 2x .
À l'aide de la calculatrice, résoudre f(x) = g(x) et f(x) \geqslant g(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
En utilisant le graphique de l'exercice 13, résoudre f(x) = 0 et f(x) \gt 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
On considère une fonction f dont la représentation graphique est donnée ci-dessous.

Décrire les variations de f sur son ensemble de définition et préciser son minimum et son maximum.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions affines
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Une fonction affine f est une fonction définie sur \R par f(x) = mx + p , où m et p sont des nombres réels.Soient a et b deux réels distincts et \mathrm{A}\left(x_{\mathrm{A}}\: ; y_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}}\: ; y_{\mathrm{B}}\right) deux points distincts de \mathcal{C}_f .
Alors : m=\dfrac{f(b)-f(a)}{b-a} et m=\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fonction f définie sur \R par f(x) = 5x - 1 est une fonction affine.Son coefficient directeur est m = 5 et son ordonnée à l'origine est p = -1 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Si m \gt 0 (resp. m \lt 0 ), alors f est une fonction strictement croissante (resp. décroissante) sur \R .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
f définie sur \R par f(x) = 3 - 5x est une fonction affine avec m = -5 \lt 0 .f est donc strictement décroissante sur \R .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Le tableau de signes de f , lorsque m \neq 0, est le suivant :

Pour étudier le signe d'un produit ou quotient de deux fonctions affines, on étudiera le signe de chacune des fonctions dans un même tableau de signes et on conclura à l'aide de la propriété des signes d'un produit ou d'un quotient.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
f est définie sur \R par f(x) = 6x - 2 .
Voici son tableau de signes :

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
f est la fonction affine définie sur \R dont on donne la représentation
graphique ci-dessous.


À l'aide du graphique :
1. déterminer le signe de f\: ;
2. déterminer l'expression de f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
f est une fonction affine telle que f(-2) = 4 et f(3) = 5 . Déterminer l'expression de f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Dresser le tableau de signes de la fonction affine f définie
par f(x) = 4 - 7x .
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Étudier le signe de la fonction f définie sur \R par :
f(x) = (2x - 5)(4 - x).
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions inverse et cube
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La fonction inverse est définie sur \mathbb{R}^{*} par f(x)=\dfrac{1}{x}.Sa courbe représentative est une hyperbole.
Voici son tableau de variations :

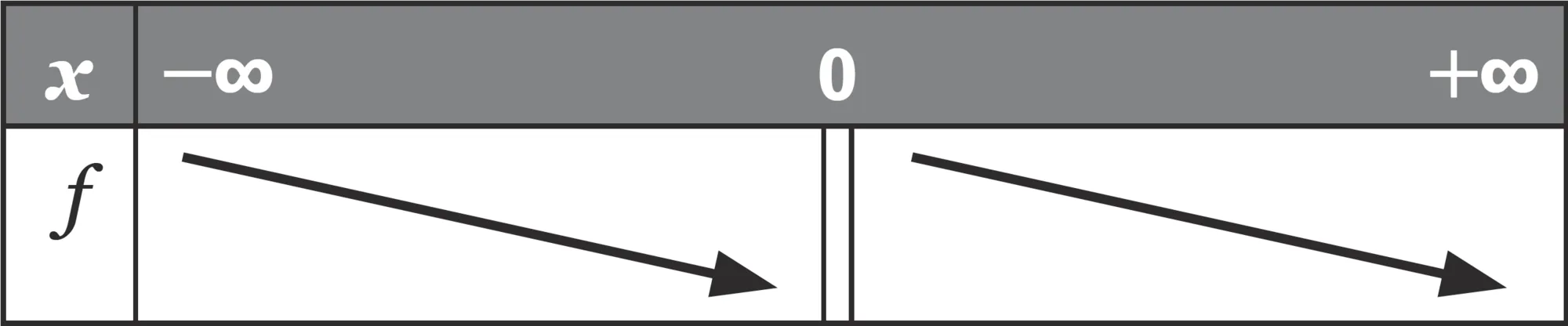
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
L'inverse de 3 est \dfrac{1}{3}.L'inverse de -\dfrac{1}{5} est -5 .
On a : 2 \leqslant 6 donc \dfrac{1}{2} \geqslant \dfrac{1}{6}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La fonction cube est définie sur \R par f(x) = x^3 .f est strictement croissante sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le cube de -3 est (-3)^3 = -27.On a : -1 \leqslant 2 donc (-1)^{3} \leqslant 2^{3}.
x^3 = 64 admet comme unique solution 4 car 4^3 = 64 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Les fonctions inverse et cube sont impaires, c'est-à-dire que, pour tout réel x de l'ensemble de définition de f , f(-x) = -f(x).Leur courbe représentative dans un repère orthonormé est une courbe symétrique par rapport à l'origine du repère.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\dfrac{1}{-7}=-\dfrac{1}{7} \:;(-5)^{3}=-\left(5^{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Comparer les réels -\dfrac{1}{5} et -\dfrac{1}{7} puis les réels 3^3 et \pi^3 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Résoudre \dfrac{1}{x}=-3 et x^3= 125.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
f est définie sur \R par f(x) = -2x^3 +\dfrac{2}{x} .
Montrer que f est une fonction impaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Résoudre \dfrac{1}{x} \geqslant 5 et x^{3}\lt27.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions carré et racine carrée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La fonction carré est définie sur \R par f(x) = x^2 .Sa courbe représentative est une parabole.
f est décroissante sur ]-\infty \: ; 0] et croissante sur [0 \: ;+\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le carré de 2 est 2^2 = 4 .Le carré de -3 est (-3)^2 = 9 .
On a : -4 \leqslant -3 donc (-4)^{2} \geqslant(-3)^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La fonction carré est paire : pour tout réel x , f(-x) = f(x).Sa courbe représentative dans un repère orthonormé est une courbe symétrique par rapport à l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
(-5)^2 = 5^2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Pour tout réel positif x , la racine carrée de x est le nombre positif, noté \sqrt{x}, tel que (\sqrt{x})^{2}=x.La fonction racine carrée est définie sur [0 \: ;+\infty[ par f(x)=\sqrt{x}.
f est strictement croissante sur [0 \: ;+\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La racine carrée de 9 est 3 .La racine carrée de -3 n'existe pas.
On a : 2 \lt 7 donc \sqrt{2}\lt\sqrt{7}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Soit a un nombre réel.On considère l'équation x^2 = a . Alors :
- si a \lt 0 , l'équation n'a pas de solution ;
- si a = 0 , l'équation a pour unique solution x = 0 ;
- si a \gt 0 , l'équation a deux solutions : x =-\sqrt{a} et x = \sqrt{a} .
On considère l'équation x^{2} \leqslant a. Alors :
- si a \lt 0 , l'inéquation n'a pas de solution ;
- si a = 0 , l'inéquation a pour unique solution x = 0 ;
- si a \gt 0 , l'ensemble des solutions est l'intervalle [-\sqrt{a}\: ; \sqrt{a}] .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
x^2 = 16 admet deux solutions -4 et 4 .x^2 = -2 n'admet pas de solution réelle.
x^2 = 0 admet comme unique solution 0 .
\left.x^{2}\lt16 \Leftrightarrow x \in\right]-4\: ; 4[.
x^{2} \leqslant-1 n'admet pas de solution réelle.
\left.\left.x^{2} \geqslant 3 \Leftrightarrow x \in\right]-\infty \: ;-\sqrt{3}\right] \cup[\sqrt{3} \: ;+\infty[.
x^{2} \geqslant-2 \Leftrightarrow x \in \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Comparer.1. \left(\dfrac{1}{2}\right)^{2} et 2^{2}.
2. \sqrt{5} et \sqrt{\pi}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Résoudre dans \R .1. \sqrt{x}=-2
2. \sqrt{x}=4
3. x^{2}=7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
f est définie sur \R par f(x) = 4 - 3x^2 .
Montrer que f est une fonction paire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Résoudre dans \R .1. \sqrt{x}\gt-2
2. x^{2} \leqslant 5
3. x^{2}>25
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

