Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 7
Activité C
Une histoire de yourte
✔ Calculer les coordonnées du vecteur somme de deux vecteurs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
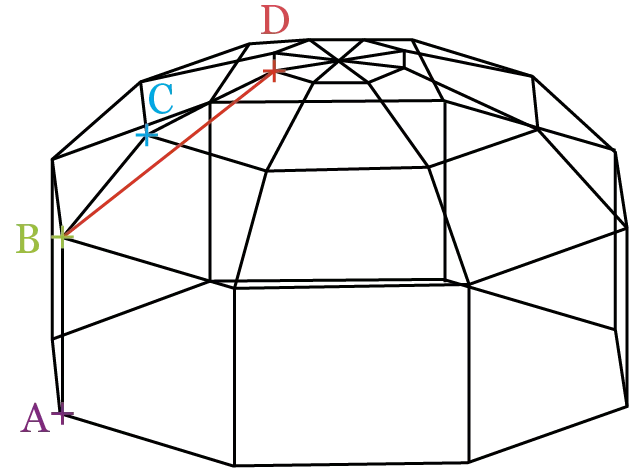
Gatien, menuisier, a été embauché pour construire la yourte modélisée ci-dessus.
Pour soutenir le toit de cette yourte, Gatien compte utiliser des planches obliques, indiquées en rouge sur le schéma. Il se demande alors de quelle longueur il doit les couper.
Toutes les planches étant identiques, Gatien décide d'en étudier une : il choisit la planche soutenant les points \mathrm{B}(6,5 \: ; 6,5 \: ; 4), \mathrm{C}(6,5 \: ; 4,5 \: ; 6) et \mathrm{D}(6,5 \: ; 1,5 \: ; 7) dont les coordonnées sont données dans un repère orthonormé. L'unité de mesure du repère est le mètre.
Problématique
De quelle taille Gatien doit-il couper les planches de support ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a.
Réaliser
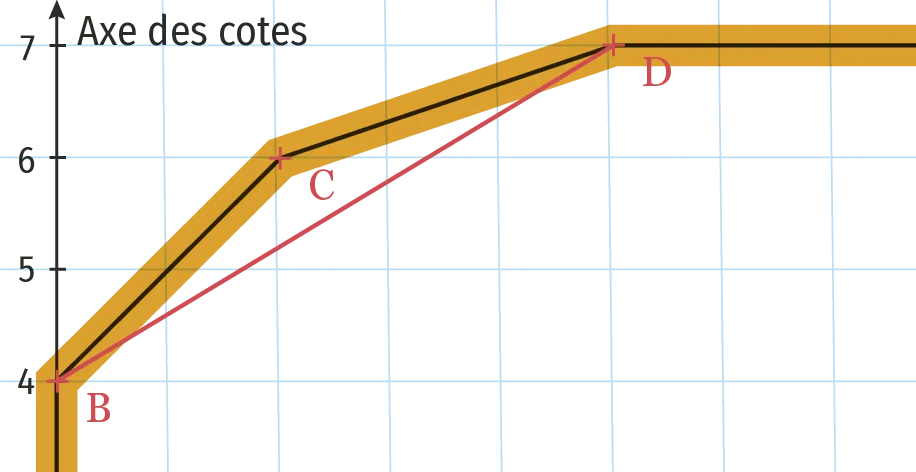
De combien de mètres se déplace‑t‑on sur l'axe des cotes lorsqu'on passe du point \text{B} au point \text{C} ? Du point \text{C} au point \text{D} ?
b. Réaliser, Analyser /Raisonner De combien de mètres se déplace‑t‑on sur l'axe des cotes lorsqu'on passe du point \text{B} au point \text{D} ? Comment aurait‑on pu trouver ce résultat à l'aide des réponses à la question précédente ?
b. Réaliser, Analyser /Raisonner De combien de mètres se déplace‑t‑on sur l'axe des cotes lorsqu'on passe du point \text{B} au point \text{D} ? Comment aurait‑on pu trouver ce résultat à l'aide des réponses à la question précédente ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Réaliser, Analyser /Raisonner
De combien de mètres se déplace-t-on sur l'axe des abscisses et sur l'axe des ordonnées lorsqu'on passe du point \text{B} au point \text{C} ? Du point \text{C} au point \text{D} ? Directement du point \text{B} au point \text{D} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
a.
Réaliser
Déterminer les coordonnées des vecteurs \overrightarrow{\mathrm{BC}} et \overrightarrow{\mathrm{CD}}.
b. Analyser /Raisonner, Réaliser Comment pourrait-on déterminer les coordonnées du vecteur \overrightarrow{\mathrm{BD}} à l'aide des coordonnées obtenues à la question précédente ? Déterminer les coordonnées de ce vecteur.
c. Communiquer, Analyser /Raisonner Compléter l'égalité entre vecteurs suivante : \overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CD}}=\ldots.
b. Analyser /Raisonner, Réaliser Comment pourrait-on déterminer les coordonnées du vecteur \overrightarrow{\mathrm{BD}} à l'aide des coordonnées obtenues à la question précédente ? Déterminer les coordonnées de ce vecteur.
c. Communiquer, Analyser /Raisonner Compléter l'égalité entre vecteurs suivante : \overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CD}}=\ldots.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
a.
Réaliser À l'aide de la réponse à la question 3. b, calculer la norme, au centimètre près, du vecteur \overrightarrow{\mathrm{BD}}.
b. Communiquer, Réaliser Répondre à la problématique.
b. Communiquer, Réaliser Répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
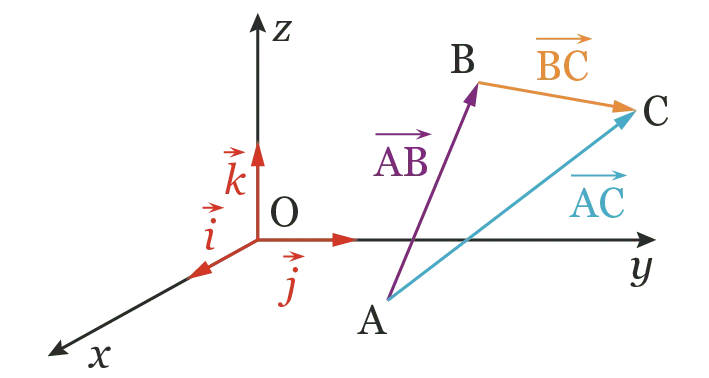
- Pour déterminer la somme de deux vecteurs, on peut utiliser la relation de Chasles : \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=
- Les coordonnées d'une somme de vecteurs sont obtenues en faisant la somme des coordonnées : {\begin{pmatrix}
x_{\overrightarrow{\mathrm{AC}}} \\
y_{\overrightarrow{\mathrm{AC}}} \\
z_{\overrightarrow{\mathrm{AC}}}
\end{pmatrix} = \begin{pmatrix}
x_{\overrightarrow{\mathrm{AB}}} + x_{\overrightarrow{\mathrm{BC}}} \\
y_{\overrightarrow{\mathrm{AB}}} + y_{\overrightarrow{\mathrm{BC}}} \\
z_{\overrightarrow{\mathrm{AB}}} + z_{\overrightarrow{\mathrm{BC}}}
\end{pmatrix}}.
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah