Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d’équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Chapitre 13
Exercices d'entraînement
Géométrie plane
15 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Reconnaître et utiliser les propriétés des translations
Définition :
Une translation est une transformation qui permet de faire glisser une figure parallèlement à une droite dans un sens donné.Remarques :
1. Dans une translation, l'image n'est ni retournée ni déformée.
2. Sur une figure, on peut schématiser par une flèche le glissement engendré par une translation.
Propriété :
Une figure et son image par translation sont superposables. Ainsi, les longueurs, les mesures d'angles, le parallélisme et les aires sont conservés.
Retrouvez et .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8[Com.1 - Com.2]
Le zoom est accessible dans la version Premium.
1. La figure 2 est l'image de la figure 1 par la
translation qui transforme le point en .
2. La figure 2 s'obtient en glissant la figure 1 sans la retourner ou la déformer parallèlement à (\mathrm{AB}) dans le sens de vers et sur la distance \text{AB}.
2. La figure 2 s'obtient en glissant la figure 1 sans la retourner ou la déformer parallèlement à (\mathrm{AB}) dans le sens de
3. La figure 1 est l'image de la figure 2 par la translation qui transforme le point en .
4. La figure 1 s'obtient en glissant la figure 2 sans la retourner ou la déformer parallèlement à (\mathrm{AB}) dans le sens de vers et sur la distance \text{AB}.
4. La figure 1 s'obtient en glissant la figure 2 sans la retourner ou la déformer parallèlement à (\mathrm{AB}) dans le sens de
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9[Mod.4]
Parmi les six figures suivantes, entourer celles qui
sont obtenues par une translation de la figure 1.Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10[Mod.4 - Com.1]
Dans les cas suivants, les figures peuvent être l'image l'une de l'autre par une translation ou obtenues par une autre transformation.1. Compléter le tableau ci-dessous en cochant les bonnes informations.
Le zoom est accessible dans la version Premium.
| Cas | Les figures sont-elles obtenues par translation ? Si non, pourquoi | |
| Oui | Non | |
| a. |
| |
| b. |
| |
| c. |
| |
| d. |
| |
2. Dans le(s) cas où la transformation est bien une translation, représenter par une flèche le déplacement permettant de passer d'une figure à l'autre.
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11[Mod.4 - Com.1]
Compléter les phrases suivantes.
Le zoom est accessible dans la version Premium.
1. Le poussin est l'image du poussin violet par la translation qui transforme \text{O} en \text{E}.
2. Le poussin bleu est l'image du poussin par la translation qui transforme \text{E} en \text{I}.
3. Le poussin est l'image du poussin rose par la translation qui transforme \text{I} en \text{O}.
2. Le poussin bleu est l'image du poussin
3. Le poussin
4. Le poussin orange est l'image du poussin bleu par la translation qui transforme en .
5. Le poussin bleu est l'image du poussin violet par la translation qui transforme en .
5. Le poussin bleu est l'image du poussin violet par la translation qui transforme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12[Rep.5 - Cal.4 - Com.4]
Le triangle \text{DEF} est l'image du triangle rectangle \text{ABC} par la translation qui transforme \text{M} en \text{N}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13[Mod.5 - Rais.4 - Com.4]
Le polygone \text{VWXYZ} est l'image de \text{ABCDE} par la translation qui transforme le point \text{R} en \text{S}.
Le zoom est accessible dans la version Premium.
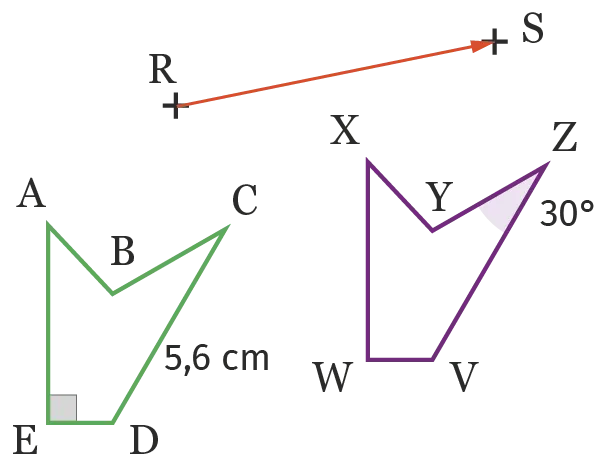
Répondre aux questions suivantes en justifiant.
1. Quelle est la longueur du segment [\mathrm{VZ}] ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 2+\left(4^{2}+1\right)=
2. 2-\left(4^{2}+1\right)=
3. 2 \times\left(4^{2}+1\right)=
4. 2 \times 4^{2}+1=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le coin des experts
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
Pour stocker le miel, les abeilles réalisent un pavage hexagonal sur les deux faces d'un cadre. Chaque face d'un cadre est constituée de \text{4~346} alvéoles, les alvéoles étant les hexagones qui constituent le pavage. Sachant qu'une alvéole peut contenir environ 269 \mathrm{~mm}^{3} de miel, quelle quantité théorique de miel, en litre, un apiculteur peut-il espérer récolter par cadre ?Coup de pouce
1 \mathrm{~L}=1 \mathrm{dm}^{3}
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah